Inflexní body tabulkovou metodou
V této podkapitole se naučíte nalézat inflexní body různých funkcí. Použitá metoda bude do jisté míry podobná metodě hledání lokálních extrémů tabulkovou metodou, tak jak byla vyložena v kapitole Monotónnost a extrémy. Opět zde platí předpoklady uvedené v podkapitole Předpoklady, kde je také vysvětlen pojem otevřený interval spojitosti první derivace, který se v celé této podkapitole využívá.
Nejprve je uvedena teorie a pak příklady a úlohy.
Teoretická část
Zvláštními body na intervalu spojitosti první derivace funkce \(f\) jsou vnitřní body tohoto intervalu, ve kterých se mění funkce z ryze konvexní na ryze konkávní nebo naopak. Těmito body jsou infexní body.
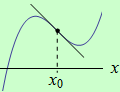
Ilustrace 1
Podívejme se na funkci \(f: y = x^3\). Druhá derivace funkce je \(f^{\prime\prime}(x) = 6x\). Vidíme, že funkce je na intervalu \((-\infty,0)\) ryze konkávní a na intervalu \((0,+\infty)\) ryze konvexní. Bod \(x = 0\), ve kterém dochází ke změně funkce z ryze konkávní na ryze konvexní je jejím inflexním bodem, viz následující obrázek.
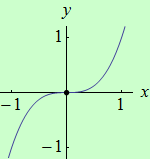
Následující definice inflexního bodu je uvedena pro úplnost.
Definice
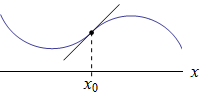
Nechť funkce \(f\) má v bodě \(x_0\) první derivaci. Přechází-li v tomto bodě graf funkce \(f\) z polohy „nad tečnou“ do polohy „pod tečnou“ nebo z polohy „pod tečnou“ do polohy „nad tečnou“, nazýváme bod \(x_0\) inflexní bod funkce \(f\).
Je-li bod \(x_0\) inflexním bodem funkce \(f\), pak bod \([x_0;f(x_0)]\) nazýváme inflexní bod grafu funkce \(f\).
Následující věta stanovuje důležité kritérium, podle kterého rozpoznáte body „podezřelé z inflexe“.
Věta
Je-li bod \(x_0\) inflexním bodem funkce \(f\) a má-li funkce \(f\) v tomto bodě druhou derivaci, pak \(f^{\prime\prime}(x_0) = 0\).
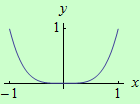
Opačné tvrzení neplatí. Je-li \(f^{\prime\prime}(x_0) = 0\), pak \(x_0\) nemusí být inflexním bodem funkce \(f\). Příkladem takové funkce je funkce \(f: y = x^4\) v bodě \(x = 0\). Funkce \(f\) je vlevo i vpravo od bodu \(x = 0\) konvexní. Bod \(x = 0\) tedy nemůže být jejím inflexním bodem, přestože \(f^{\prime\prime}(0) = 0\), viz obrázek:
Pomocí následující věty budeme určovat inflexní body.
Věta
Nechť funkce \(f\) je definovaná a má spojitou první derivaci v nějakém okolí bodu \(x_0\).
Pokud je funkce v nějakém levém okolí bodu \(x_0\) ryze konvexní a v nějakém pravém okolí bodu \(x_0\) ryze konkávní, pak má v bodě \(x_0\) inflexní bod.
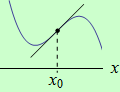
Pokud je funkce v nějakém levém okolí bodu \(x_0\) ryze konkávní a v nějakém pravém okolí bodu \(x_0\) ryze konvexní, pak má v bodě \(x_0\) inflexní bod.
Tabulková metoda pro hledání inflexních bodů:
- Využije se stejné metody jako při hledání intervalů ryzí konvexnosti a ryzí konkávnosti s tím, že se navíc uplatní výše uvedená věta.
- Pozor: Omezíme-li v zadání interval, na kterém je funkce zkoumána, bereme to jako omezení definičního oboru dané funkce. Proto tomu také přizpůsobíme otevřené intervaly spojitosti první derivace, viz Příklad 4 a Příklad 5.
Příklady a úlohy
Značení
V následujících příkladech a úlohách budeme používat tato značení:
| BN2D | ..... | body z otevřených intervalů spojitosti první derivace, v nichž je druhá derivace funkce nulová, a body, v nichž není druhá derivace definována; (jako „body nulové druhé derivace“ a „body nedefinované druhé derivace“). |
| IB | ..... | inflexní bod; |
| KBS | ..... | levé krajní body intervalů spojitosti první derivace, v nichž je funkce zprava spojitá, a pravé krajní body intervalů spojitosti první derivace, v nichž je funkce zleva spojitá; (jako „krajní body spojitosti“); |
Příklad 1
Určete intervaly, ve kterých je funkce \(f: y = x^3-6x^2+2x\) ryze konvexní a ryze konkávní, a určete její inflexní body.
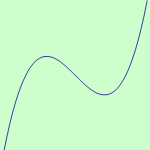 schéma grafu funkce |
První derivace: \(f^{\prime}(x) = 3x^2-12x+2\).
Otevřené intervaly spojitosti první derivace: \((-\infty,+\infty)\).
KBS: žádné.
Druhá derivace: \(f^{\prime\prime}(x) = 6x-12=6(x-2)\).
BN2D: 2.
Tabulka:
| \((-\infty,2)\) | \(2\) | \((2,+\infty)\) |
|---|---|---|
| \(f^{\prime\prime}(1) = -6 \lt 0\) ryze konkávní |
IB |
\(f^{\prime\prime}(3) = 6 \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konkávní na intervalu \((-\infty,2 \rangle \), ryze konvexní na intervalu \( \langle 2,+\infty)\) a má inflexní bod \(x = 2\).
Úloha 1
Určete intervaly, ve kterých je funkce \(f: y = -x^3+3x^2+1\) ryze konvexní a ryze konkávní, a určete její inflexní body.
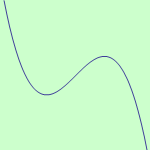 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Příklad 2
Určete intervaly, ve kterých je funkce \(f: y = x^4-6x^2+3x\) ryze konvexní a ryze konkávní, a určete její inflexní body.
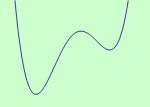 schéma grafu funkce |
První derivace: \(f^{\prime}(x) = 4x^3-12x+3\).
Otevřené intervaly spojitosti první derivace: \((-\infty,+\infty)\).
KBS: žádné.
Druhá derivace: \(f^{\prime\prime}(x) = 12x^2-12=12(x^2-1)=12(x-1)(x+1)\).
BN2D: -1; 1.
Tabulka:
| \((-\infty,-1)\) | \(-1\) | \((-1,1)\) | \(1\) | \((1,+\infty)\) |
|---|---|---|---|---|
| \(f^{\prime\prime}(-2) = 36 \gt 0\) ryze konvexní |
IB |
\(f^{\prime\prime}(0) = -12 \lt 0\) ryze konkávní |
IB |
\(f^{\prime\prime}(2) = 36 \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konvexní na intervalech \((-\infty,-1 \rangle \) a \( \langle 1,+\infty)\), ryze konkávní na intervalu \( \langle {-1},1 \rangle \) a má dva inflexní body \(x \in \{-1,1\}\).
Úloha 2
Určete intervaly, ve kterých je funkce \(f: y = -x^4-4x^3+3\) ryze konvexní a ryze konkávní, a určete její inflexní body.
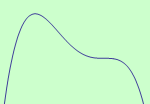 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Příklad 3
Určete intervaly, ve kterých je funkce \(f: y = (x-2) \large e^x\) ryze konvexní a ryze konkávní, a určete její inflexní body.
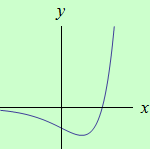 schéma grafu funkce |
První derivace: \(f^{\prime}(x) = (x-1) \large e^x\).
Otevřené intervaly spojitosti první derivace: \((-\infty,+\infty)\).
KBS: žádné.
Druhá derivace: \(f^{\prime\prime}(x) = x \large e^x\).
BN2D: 0.
Tabulka:
| \((-\infty,0)\) | \(0\) | \((0,+\infty)\) |
|---|---|---|
| \(f^{\prime\prime}(-1) = -{\large e^{-1}} \lt 0\) ryze konkávní |
IB |
\(f^{\prime\prime}(1) = {\large e} \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konkávní na intervalu \((-\infty,0 \rangle \), ryze konvexní na intervalu \( \langle 0,+\infty)\) a má inflexní bod \(x = 0\).
Úloha 3
Určete intervaly, ve kterých je funkce \(f: y = x \large e^x\) ryze konvexní a ryze konkávní, a určete její inflexní body.
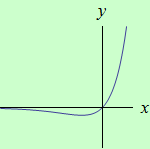 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Úloha 4
Určete intervaly, ve kterých je funkce \(f: y = (x^2-3x+2)\large e^x\) ryze konvexní a ryze konkávní, a určete její inflexní body.
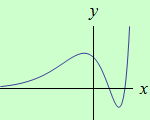 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Příklad 4
Určete intervaly, ve kterých je funkce \(f: y = \cos{x}\) s definičním oborem \(D(f) = \langle {-\pi},\pi \rangle \) ryze konvexní a ryze konkávní, a určete její inflexní body.
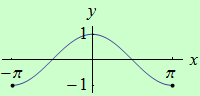 graf funkce |
První derivace: \(f^{\prime}(x) = -\sin{x}\).
Otevřené intervaly spojitosti první derivace: \((-\pi,\pi)\).
KBS: \(-\pi, \pi\).
Druhá derivace: \(f^{\prime\prime}(x) = -\cos{x}\).
BN2D: \(\large -\frac{\pi}{2}, \frac{\pi}{2}\).
Tabulka:
| \(-\pi\) | \((-\pi,-\dfrac{\pi}{2})\) | \(-\dfrac{\pi}{2}\) | \((-\dfrac{\pi}{2},\dfrac{\pi}{2})\) | \(\dfrac{\pi}{2}\) | \((\dfrac{\pi}{2},\pi)\) | \(\pi\) |
|---|---|---|---|---|---|---|
| \(f^{\prime\prime}(-\pi) = 1 \gt 0\) ryze konvexní |
IB |
\(f^{\prime\prime}(0) = -1 \lt 0\) ryze konkávní |
IB |
\(f^{\prime\prime}(\pi) = 1 \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konvexní na intervalech \( \langle {-\pi},-\dfrac{\pi}{2} \rangle \) a \( \langle \dfrac{\pi}{2},\pi \rangle \), ryze konkávní na intervalu \( \langle {-\dfrac{\pi}{2}},\dfrac{\pi}{2} \rangle \) a má dva inflexní body \(x \in \{-\dfrac{\pi}{2}, \dfrac{\pi}{2} \}\).
Poznámka
Asi jste si všimli, že jsme konvexnost/konkávnost funkce \(f\) na intervalech \((-\pi,-\dfrac{\pi}{2})\) a \((\dfrac{\pi}{2},\pi)\) testovali pomocí hodnoty druhé derivace v krajních bodech, které do těchto intervalů nepatří. Tento postup je povolený za předpokladu, že je druhá derivace v krajním bodě definovaná a nenulová.
Úloha 5
Určete intervaly, ve kterých je funkce \(f: y = \sin{x}\) s definičním oborem \(D(f) = \langle {-\pi},\pi \rangle \) ryze konvexní a ryze konkávní, a určete její inflexní body.
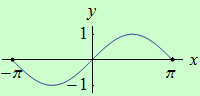 graf funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Příklad 5
Určete intervaly, ve kterých je funkce \(f: y = {\rm tg}\:x\) s definičním oborem \(D(f) = ({-\dfrac{\pi}{2}},\dfrac{\pi}{2})\) ryze konvexní a ryze konkávní, a určete její inflexní body.
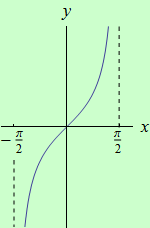 graf funkce |
První derivace: \(f^{\prime}(x) = \dfrac{1}{\cos^2{x}}\).
Otevřené intervaly spojitosti první derivace: \(({-\dfrac{\pi}{2}},\dfrac{\pi}{2})\).
KBS: žádné.
Druhá derivace: \(f^{\prime\prime}(x) = \dfrac{2\sin{x}}{\cos^3{x}}\).
BN2D: 0.
Tabulka:
| \((-\dfrac{\pi}{2},0)\) | \(0\) | \((0,\dfrac{\pi}{2})\) |
|---|---|---|
| \(f^{\prime\prime}(-\dfrac{\pi}{4}) = -4 \lt 0\) ryze konkávní |
IB |
\(f^{\prime\prime}(\dfrac{\pi}{4}) = 4 \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konkávní na intervalu \(({-\dfrac{\pi}{2}},0 \rangle \), ryze konvexní na intervalu \( \langle 0,\dfrac{\pi}{2})\) a má inflexní bod \(x = 0\).
Úloha 6
Určete intervaly, ve kterých je funkce \(f: y = {\rm cotg}\:x\) s definičním oborem \(D(f) = (0,\pi)\) ryze konvexní a ryze konkávní, a určete její inflexní body.
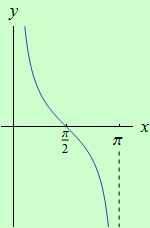 graf funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
Druhá derivace:
Tabulka:
Závěr:
Úloha 7
Určete intervaly, ve kterých je funkce \(f: y = \dfrac{1}{x}+\ln{x}\) ryze konvexní a ryze konkávní, a určete její inflexní body.
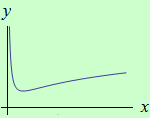 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
Druhá derivace:
Tabulka:
Závěr:
Úloha 8
Určete intervaly, ve kterých je funkce \(f: y = \dfrac{1}{x}+x^2\) ryze konvexní a ryze konkávní, a určete její inflexní body.
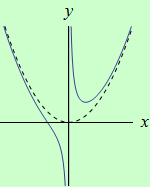 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
Druhá derivace:
Dvě tabulky:
|
|
|
Závěr:
Úloha 9
Určete intervaly, ve kterých je funkce \(f: y = -x |x|\) ryze konvexní a ryze konkávní, a určete její inflexní body.
Tato úloha navazuje na Příklad 5 z předchozí podkapitoly.
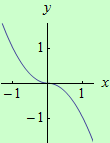 graf funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
| Druhá derivace: \(f^{\prime\prime}(x) =\;\) | |
Tabulka:
Závěr:
