Od sečny k tečně
Připomeňme si, že v rovině se směrnice přímky, která není svislá, vypočítá jako tangens směrového úhlu, který tato přímka svírá s kladnou poloosou x, jak ukazuje následující obrázek. Tento úhel může nabývat hodnoty pouze z intervalu \langle 0, \pi ).
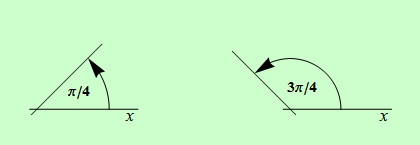
ilustrační obrázek - směrový úhel
Aplet - příklady tečen
V následujícím apletu pohybujte bodem x_0 po ose x a sledujte změnu polohy tečny a změnu její směrnice. Zaškrtnete-li volitelnou možnost konstrukce směrnice, uvidíte, jak hodnotu směrnice vyčíst z grafu tečny. V pravoúhlém trojúhelníku, který se ukáže, je délka odvěsny, která je vodorovná, rovna jedné a délka odvěsny, která je svislá, je proto rovna tangensu úhlu u vrcholu v bodě T. Velikost směrnice tečny vedené bodem T je tedy rovna délce odvěsny, která je svislá. Znaménko směrnice je pak kladné, je-li přepona nad odvěsnou, která je vodorovná, a je záporné, je-li přepona pod touto odvěsnou.
Pod apletem si můžete vybrat jednu z následujících funkcí: \Large\frac{x^3}{4}, x^2, \sin{x}, \Large\frac{\sin{2x}}{2} + x.
Poznámka
U lineární funkce je tečnou v kterémkoliv bodě jejího grafu přímka splývající s grafem této funkce.
Intuitivní představu o tom, jak vypadá tečna ke křivce, jež je grafem funkce, již máte. Jaká je rovnice takové tečny? A kdy tato rovnice vůbec existuje? Rovnici tečny sestavíme na základě dvou údajů: bodu, v němž tečnu ke grafu funkce konstruujeme, a její směrnice. 
Tečnami, které nemají směrnici, tj. svislými tečnami, se nebudeme v tomto textu zabývat.
Aplet - sečna a tečna
V následujícím apletu můžete pohybovat bodem x_0 po ose x a posuvníkem v pravém horním rohu určujícím hodnotu \Delta x = x_1-x_0 (čti „delta x“). Sledujte, jak je rozdíl směrnic sečny a tečny menší, čím blíž jsou u sebe body x_0 a x_1.
Nechť je dán graf funkce f. Směrnici tečny ke grafu v bodě T = [x_0;f(x_0)] vypočítáme jako limitu směrnice sečny procházející body T a S = [x_1;f(x_1)], pro x_1 \to x_0, za předpokladu, že tato limita existuje a je vlastní.
Rovnice sečny
Prochází-li přímka s dvěma různými body [x_0;y_0] a [x_1;y_1], které leží na grafu funkce f, pak se jedná o sečnu tohoto grafu a její rovnice je
y - y_0 \; = \; k_s \cdot (x - x_0) ,
kde k_s \; = \; \Large\frac{y_1 - y_0}{x_1 - x_0} \normalsize\; = \; \Large\frac{f(x_1) - f(x_0)}{x_1 - x_0} je směrnice této sečny.
Rovnice tečny
Mějme funkci f definovanou v jistém okolí bodu x_0. Je-li limita
\Large\lim\limits_{x_1 \to x_0} \frac{f(x_1) - f(x_0)}{x_1 - x_0}
vlastní, pak je směrnicí tečny ke grafu funkce f vedené bodem T = [x_0;f(x_0)]. Označíme-li tuto směrnici jako k_T, pak rovnice tečny má tvar
y - f(x_0) \; = \; k_T \cdot (x - x_0) .
Využijeme-li obvyklého značení, že \Delta x = x_1 - x_0, kde x_0 je pevně dané, pak platí
\Large\lim\limits_{x_1 \to x_0} \frac{f(x_1) - f(x_0)}{x_1 - x_0} \normalsize\; = \; \Large\lim\limits_{\Delta x \to 0} \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x} .
