Příklad 7: Vitráž
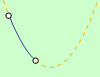
Je dáno čtvrecové okno široké a vysoké 4 m. Okno se má zasklít pomocí modrého a zeleného skla tak, aby vypadalo jako v následujícím apletu. Cena modrého skla je 100 Kč za metr čtvereční a cena zeleného skla je 120 Kč za metr čtvereční.
Jakou hodnotu musí mít \(x\) (viz aplet), aby celková cena za sklo byla nejnižší, a jaká cena to bude?
Řešení
1. Nejdříve identifikujeme proměnnou, jejíž extrém budeme hledat, a typ extrému (maximum nebo minimum).
Minimalizujeme cenu skla. Označme tuto proměnnou písmenem \(c\) (jako cena).
Množství modrého skla v \({\rm m^2}\) je \(2x(4-x) + x(4-2x) = 4(3x-x^2).\)
Cena za modré sklo v Kč je \(400(3x-x^2).\)
Množství zeleného skla v \({\rm m^2}\) je \(2x^2+(4-x)(4-2x) = 4(x^2-3x+4).\)
Cena za zelené sklo v Kč je \(120\cdot 4(x^2-3x+4).\)
Celková cena v Kč je po úpravě
\(c = 80(x^2-3x+24).\)
2. Ze vztahů mezi proměnnými docílíme jejich redukce tak, aby proměnná, jejíž extrém hledáme, závisela jen na jedné nezávislé proměnné.
Zde nemusíme nic redukovat, neboť proměnná \(c\) závisí pouze na proměnné \(x.\)
3. Dále určíme definiční obor nezávislé proměnné \(x\), na níž závisí proměnná \(c\), jejíž extrém hledáme.
Z rozměrů barevných částí okna je zřejmé, že definiční obor proměnné \(x\) je
\(x \in ( 0, 2 )\).
4. Nyní přepíšeme vztah \(c = 80(x^2-3x+24)\) pro \(x \in ( 0, 2 )\) do tvaru funkčního předpisu. Místo proměnné \(c\) napíšeme \(f(x)\). Z definičního oboru proměnné \(x\) stanovíme definiční obor funkce \(f.\)
\(f(x) = 80(x^2-3x+24)\) s definičním oborem \(D(f) = ( 0, 2) .\)
5. Najdeme hledaný extrém.
Hledáme globální minimum. Platí, že \(f^{\prime}(x) = 80 (2 x - 3).\)
Vzhledem k tomu, že funkce \(f\) má definovanou derivaci na celém intervalu \(( 0, 2 )\), tak body „podezřelými z extrému“ jsou pouze stacionární body funkce \(f\).
Stacionární body splňuji rovnici \(80 (2 x - 3) = 0\). Řešením z definičního oboru funkce \(f\) je
\(x = 3/2 = 1{,}5.\)
Ověříme, zda má funkce \(f\) ve stacionárním bodě \(x = 1{,}5\) globální minimum.
Funkce \(f\) je na intervalu \(( 0, 2 )\) spojitá. Její derivace je na tomto intervalu všude definovaná. Navíc tam má jediný stacionární bod \(x = 1{,}5\).
K stanovení průběhu funkce \(f\) použijeme tabulkovou metodu z kapitoly Monotónnost a extrémy, podkapitoly Lokální extrémy tabulkovou metodou.
| \((0;1{,}5)\) | \(1{,}5\) | \((1{,}5; 2)\) |
|---|---|---|
| \(f^{\prime}(1) = -80 \lt 0\) klesající |
m |
\(f^{\prime}(2) = 80 \gt 0\) rostoucí |
| Poznámka: | V tabulce je testování první derivace v krajním bodě intervalu povoleno za předpokladu, že je tam tato derivace definovaná a nenulová. |
Z průběhu funkce \(f\) je zřejmé, že lokální minimum v bodě \(x = 1{,}5\) je i globálním minimem.
Poznámka: Hledání globálního minima bez využití derivací. 
6. Zapíšeme řešení.
Sklo pro vitráž je nejlevnější pro \(x = 1{,}5 \; {\rm m}.\)
Cena skla by byla \(f(1{,}5) = 1740\) Kč.
Odkazy na příklady