Konvexnost a konkávnost tabulkovou metodou


„Do konkávní kávy nenaleješ.“
V této podkapitole se naučíte nalézat tabulkovou metodou intervaly ryzí konvexnosti a ryzí konkávnosti pro různé funkce. Použitá metoda bude do jisté míry podobná metodě hledání intervalů monotónnosti tabulkovou metodou, tak jak byla vyložena v kapitole Monotónnost a extrémy. Platí zde předpoklady uvedené v podkapitole Předpoklady, kde je také vysvětlen pojem otevřený interval spojitosti první derivace, který se v celé této podkapitole využívá.
Nejprve je uvedena teorie a pak příklady a úlohy.
Teoretická část
Definice
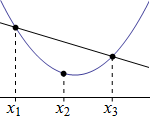 ryze konvexní |
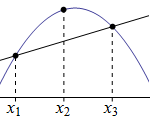 ryze konkávní |
Funkce \(f\) se nazývá ryze konvexní v intervalu \(I\), právě když pro libovolná čísla \(x_1, x_2, x_3 \in I\), která splňují nerovnost \(x_1 \lt x_2 \lt x_3\), platí, že bod \([x_2;f(x_2)]\) leží pod přímkou procházející body \([x_1;f(x_1)]\) a \([x_3;f(x_3)]\).
Funkce \(f\) se nazývá ryze konkávní v intervalu \(I\), právě když pro libovolná čísla \(x_1, x_2, x_3 \in I\), která splňují nerovnost \(x_1 \lt x_2 \lt x_3\), platí, že bod \([x_2;f(x_2)]\) leží nad přímkou procházející body \([x_1;f(x_1)]\) a \([x_3;f(x_3)]\).
V případě, že připustíme možnost, aby bod \([x_2;f(x_2)]\) z předcházející definice ležel na přímce procházející body \([x_1;f(x_1)]\) a \([x_3;f(x_3)]\), pak hovoříme o funkci konvexní v intervalu \(I\), resp. o funkci konkávní v intervalu \(I\) (obojí bez přívlastku „ryzí“).
Ilustrace 1
Na následujících obrázcích jsou zobrazeny grafy ryze konvexní a ryze konkávní funkce. Všimněte si, že sestrojíme-li tečnu ke grafu ryze konvexní funkce, leží body grafu této funkce nad touto tečnou s výjimkou bodu dotyku. Podobně sestrojíme-li tečnu ke grafu ryze konkávní funkce, leží body grafu této funkce pod touto tečnou s výjimkou bodu dotyku.
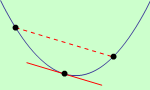 ryze konvexní |
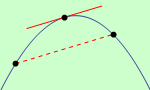 ryze konkávní |
Od uvedené ilustrace se dostáváme k následující definici:
Definice
Funkce \(f\) se nazývá ryze konvexní v bodě \(x_0\), jestliže má v bodě \(x_0\) derivaci a jestliže existuje takové číslo \(\delta \gt 0\), tak, že pro každé \(x \in (x_0-\delta,x_0) \cup (x_0,x_0+\delta)\) platí:
bod \([x;f(x)]\) leží nad tečnou vedenou bodem \([x_0;f(x_0)]\).
Funkce \(f\) se nazývá ryze konkávní v bodě \(x_0\), jestliže má v bodě \(x_0\) derivaci a jestliže existuje takové číslo \(\delta \gt 0\), tak, že pro každé \(x \in (x_0-\delta,x_0) \cup (x_0,x_0+\delta)\) platí:
bod \([x;f(x)]\) leží nad tečnou vedenou bodem \([x_0;f(x_0)]\).
Poznámka k definici
Věta
Je-li \(f^{\prime\prime}(x_0) \gt 0\), pak je funkce \(f\) ryze konvexní v bodě \(x_0\).
Je-li \(f^{\prime\prime}(x_0) \lt 0\), pak je funkce \(f\) ryze konkávní v bodě \(x_0\).
Poznámka k větě
Věta
Je-li funkce ryze konvexní v každém bodě otevřeného intervalu I, pak je v tomto intervalu ryze konvexní.
Je-li funkce ryze konkávní v každém bodě otevřeného intervalu I, pak je v tomto intervalu ryze konkávní.
Následující věta je důležitá pro aplikaci tabulkové metody.
Věta
Má-li funkce \(f\) v každém bodě otevřeného intervalu \((a,b)\) nenulovou druhou derivaci, pak tam má tato druhá derivace stále stejné znaménko. To znamená, že je funkce \(f\) na tomto intervalu buď jen ryze konvexní, nebo jen ryze konkávní.
Poznámka k předchozí větě
To, zda je funkce ryze konvexní, nebo ryze konkávní, lze ověřit pomocí hodnoty druhé derivace v libovolném jednom bodě tohoto otevřeného intervalu. Na tom je založena tzv. tabulková metoda pro hledání intervalů ryzí konvexnosti a ryzí konkávnosti.
Tabulková metoda pro určování intervalů ryzí konvexnosti a ryzí konkávnosti:
Tisková verze je k dispozici >zde<.
- Nejprve vypočítáme první derivaci dané funkce.
- Poté stanovíme otevřené intervaly spojitosti první derivace funkce. Tyto intervaly jsou vysvětleny v podkapitole Předpoklady.
- Z levých krajních bodů otevřených intervalů spojitosti první derivace stanovíme body, v nichž je funkce zprava spojitá, a z pravých krajních bodů těchto intervalů stanovíme body, v nichž je funkce zleva spojitá.
- Vypočítáme druhou derivaci funkce.
- Stanovíme body z otevřených intervalů spojitosti první derivace, ve kterých je druhá derivace nulová, nebo v nichž není definována.
- Pro každý otevřený interval spojitosti první derivace sestavíme samostatnou tabulku podle následujících tří bodů.
- Je-li funkce v levém krajním bodě intervalu zprava spojitá, zapíšeme tento bod zleva do záhlaví tabulky. Podobně, je-li funkce v pravém krajním bodě intervalu zleva spojitá, zapíšeme tento bod zprava do záhlaví příslušné tabulky.
- Každý otevřený interval spojitosti první derivace dále rozdělíme pomocí bodů, v nichž je druhá derivace nulová, a bodů, v nichž není druhá derivace definována, na otevřené intervaly, a tyto body a intervaly uvedeme do záhlaví příslušné tabulky.
- Pro každý interval v záhlaví tabulky otestujeme v jednom libovolném bodě tohoto intervalu znaménko druhé derivace, a podle přechozích vět stanovíme, zda je tam funkce ryze konvexní nebo ryze konkávní. To uvedeme v tabulce.
- V závislosti na situaci případně využijeme následující větu:
Věta
Nechť má funkce spojitou první derivaci na otevřeném intervalu \((a,b)\) a nechť \(c \in (a,b)\). Pokud je funkce ryze konvexní na intervalech \((a,c)\) a \((c,b)\), pak je ryze konvexní i na intervalu \((a,b)\). Pokud je funkce ryze konkávní na intervalech \((a,c)\) a \((c,b)\), pak je ryze konkávní i na intervalu \((a,b)\).
Je-li funkce ryze konvexní, resp. ryze konkávní na otevřeném intervalu \((a,b)\) a spojitá na intervalu \( \langle a,b)\), pak je ryze konvexní, resp. ryze konkávní i na intervalu \( \langle a,b)\). Obdobně pro interval \((a,b \rangle \).
Je-li funkce ryze konvexní, resp. ryze konkávní na otevřeném intervalu \((a,b)\) a spojitá na intervalu \( \langle a,b \rangle \), pak je ryze konvexní, resp. ryze konkávní i na intervalu \( \langle a,b \rangle \).
Ilustrace 2
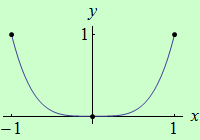
Zkoumejme funkci \(f: y = x^4\) na intervalu \( \langle {-1},1 \rangle \). Otevřený interval spojitosti první derivace je \({(}{-1},1{)}\). Druhá derivace funkce je \(f^{\prime\prime}(x) = 12x^2\). Vidíme, že funkce je na intervalech \((-1,0)\) a \((0,1)\) ryze konvexní, neboť tam je \(f^{\prime\prime}(x) \gt 0\). V bodě \(x = 0\) je druhá derivace nulová. Podle předchozí věty je tedy funkce ryze konvexní na intervalu \((-1,1)\). Protože je funkce spojitá na intervalu \( \langle {-1},1 \rangle \), je podle předchozí věty ryze konvexní i na tomto intervalu.
Příklady a úlohy
Značení
V následujících příkladech a úlohách budeme používat tato značení:
| BN2D | ..... | body z otevřených intervalů spojitosti první derivace, v nichž je druhá derivace funkce nulová, a body, v nichž není druhá derivace definována; (jako „body nulové druhé derivace“ a „body nedefinované druhé derivace“). |
| KBS | ..... | levé krajní body otevřených intervalů spojitosti první derivace, v nichž je funkce zprava spojitá, a pravé krajní body intervalů spojitosti první derivace, v nichž je funkce zleva spojitá; (jako „krajní body spojitosti“); |
Příklad 1
Určete intervaly, ve kterých je funkce \(f: y = 4x^2 - x + 5\) ryze konvexní a ryze konkávní.
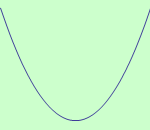 schéma grafu funkce |
První derivace: \(f^{\prime}(x) = 8x - 1\).
Otevřené intervaly spojitosti první derivace: \((-\infty,+\infty)\).
KBS: žádné.
Druhá derivace: \(f^{\prime\prime}(x) = 8\).
BN2D: žádné.
Tabulka:
| \((-\infty,+\infty)\) |
|---|
| \(f^{\prime\prime}(0) = 8 \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konvexní na intervalu \((-\infty,+\infty)\).
Úloha 1
Určete intervaly, ve kterých je funkce \(f: y = -2x^2 + 3x + 1\) ryze konvexní a ryze konkávní.
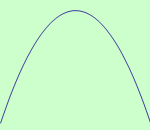 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Poznámka:
Úloha 2
Určete intervaly, ve kterých je funkce \(f: y = \large e^x\) ryze konvexní a ryze konkávní.
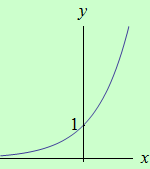 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Příklad 2
Určete intervaly, ve kterých je funkce \(f: y = \sqrt{x}\) ryze konvexní a ryze konkávní.
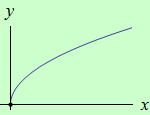 schéma grafu funkce |
První derivace: \(f^{\prime}(x) = \dfrac{1}{2\sqrt{x}}\).
Otevřené intervaly spojitosti první derivace: \((0,+\infty)\).
KBS: 0.
Druhá derivace: \(f^{\prime\prime}(x) = -\dfrac{1}{4\sqrt{x^3}}\).
BN2D: žádné.
Tabulka:
| \(0\) | \((0,+\infty)\) |
|---|---|
| \(f^{\prime\prime}(1) = -\dfrac{1}{4} \lt 0\) ryze konkávní |
Závěr: Funkce \(f\) je ryze konkávní na intervalu \( \langle 0,+\infty)\).
Úloha 3
Určete intervaly, ve kterých je funkce \(f: y = \ln{x}\) ryze konvexní a ryze konkávní.
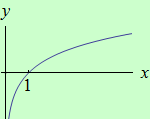 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
Druhá derivace:
Tabulka:
Závěr:
Příklad 3
Určete intervaly, ve kterých je funkce \(f: y = \dfrac{1}{x}\) ryze konvexní a ryze konkávní.
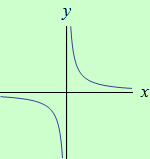 schéma grafu funkce |
První derivace: \(f^{\prime}(x) = -\dfrac{1}{x^2}\).
Otevřené intervaly spojitosti první derivace: \((-\infty,0)\) a \((0,+\infty)\).
KBS: žádné.
Druhá derivace: \(f^{\prime\prime}(x) = \dfrac{2}{x^3}\).
BN2D: žádné.
Dvě tabulky: jedna pro interval \((-\infty,0)\) a druhá pro interval \((0,+\infty)\).
|
|
Závěr: Funkce \(f\) je ryze konkávní na intervalu \((-\infty,0)\) a ryze konvexní na intervalu \((0,+\infty)\).
Úloha 4
Určete intervaly, ve kterých je funkce \(f: y = \dfrac{1}{x^2}\) ryze konvexní a ryze konkávní.
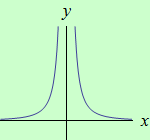 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
Druhá derivace:
Dvě tabulky:
|
|
|
Závěr:
Příklad 4
Určete intervaly, ve kterých je funkce \(f: y = (x^2-4x+6) \large e^x\) ryze konvexní a ryze konkávní.
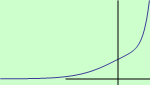 schéma grafu funkce |
První derivace: \(f^{\prime}(x) = (x^2-2x+2) \large e^x\).
Otevřené intervaly spojitosti první derivace: \((-\infty,+\infty)\).
KBS: žádné.
Druhá derivace: \(f^{\prime\prime}(x) = x^2 \large e^x\).
BN2D: 0.
Tabulka:
| \((-\infty,0)\) | \(0\) | \((0,+\infty)\) |
|---|---|---|
| \(f^{\prime\prime}(-1) = {\large e^{-1}} \gt 0\) ryze konvexní |
\(f^{\prime\prime}(1) = {\large e} \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konvexní na intervalu \((-\infty,+\infty)\).
Úloha 5
Určete intervaly, ve kterých je funkce \(f: y = (x^2-2x+3) \large e^x\) ryze konvexní a ryze konkávní.
 schéma grafu funkce |
První derivace:
Otevřené intervaly spojitosti první derivace:
KBS:
Druhá derivace:
BN2D:
Tabulka:
Závěr:
Příklad 5
Určete intervaly, ve kterých je funkce \(f: y = x |x|\) ryze konvexní a ryze konkávní.
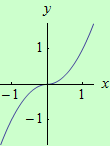 graf funkce |
Řešení
První derivace: \(f^{\prime}(x) = 2|x|\) .
.Otevřené intervaly spojitosti první derivace: \((-\infty,+\infty)\).
KBS: žádné.
| Druhá derivace: \(f^{\prime\prime}(x) =\;\) | -2 pro \(x \lt 0\), |
| 2 pro \(x \gt 0\), | |
| nedefinována pro \(x = 0\). |
Tabulka:
| \((-\infty,0)\) | \(0\) | \((0,+\infty)\) |
|---|---|---|
| \(f^{\prime\prime}(-1) = -2 \lt 0\) ryze konkávní |
\(f^{\prime\prime}(1) = 2 \gt 0\) ryze konvexní |
Závěr: Funkce \(f\) je ryze konkávní na intervalu \((-\infty,0 \rangle\) a ryze konvexní na intervalu \(\langle 0,+\infty)\).
