Kacov 2011

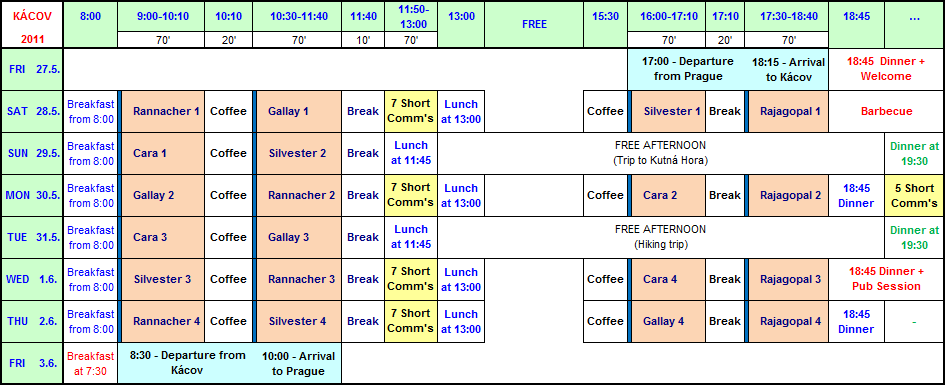
The schedule of the conference

Each main lecturer gives a series of four lectures, each 70 minutes long.
The participants can present their results in the framework of
Short Communications (10 minutes each, including discussion)
and within the reprint and preprint exhibition.

The detailed program of the school
The program can be changed during the conference. See the posted information on the conference place.

Abstracts of main lectures

Enrique Fernández Cara
Dpto. Ecuaciones Diferenciales y Analisis Numerico
Facultad de Matematicas
Universidad de Sevilla
41080 Sevilla, Spain
email: cara (at) us.es
home: http://investigacion.us.es/sisius/sis_showpub.php?idpers=965
The variable density Navier-Stokes equations and some related topics

Abstract:
This series of lectures is devoted to analyze Newtonian incompressible non-homogeneous fluids. These are governed by the so called variable density Navier-Stokes equations. I will try to recall the main theoretical results that can be obtained for initial-boundary value problems for these equations. I will also consider some related control problems. Finally, some interesting open questions of variable difficulty level will be mentioned. The plan is the following:

Physical motivation and basic existence results for the initial-boundary value problem.
Strong solutions, regularity and uniqueness.
Control problems and applications.
Some additional remarks and open questions.

Files for download:

Lecture 1:       Lecture 2:       Lecture 3:       Lecture 4:

Thierry Gallay
Institut Fourier
Université de Grenoble I
38402 Saint-Martin-d'Hères
France
email: Thierry.Gallay (at) ujf-grenoble.fr
home: http://www-fourier.ujf-grenoble.fr/~gallay/
Stability and interaction of vortices in two-dimensional viscous flows

Abstract:
The goal of these lectures is to present a few rigorous results which illustrate the role played by vortices in the dynamics of two-dimensional viscous flows. The lectures will be organized as follows:

The Cauchy problem for the two-dimensional vorticity equation in the space of finite measures. In this introductory lecture, classical existence results for solutions of the 2D Navier-Stokes equation will be reviewed. We shall see why they fail to prove uniqueness of the solution when the initial data contain large point vortices.
Self-similar variables, Lyapunov functions, and long-time behavior. Using ideas from the theory of dynamical systems, we shall prove that all integrable solutions of the 2D vorticity equation converge to Oseen vortices as time goes to infinity. The same approach allows to overcome the difficulty mentioned in the first lecture.
Asymptotic stability of Oseen vortices. Before studying vortex interactions, it is important to understand the stability properties of a single isolated vortex. The linearized operator at Oseen's vortex has a relatively simple structure but displays interesting spectral and pseudo-spectral phenomena in the limit where the circulation Reynolds number becomes large.
Interaction of vortices in weakly viscous flows. To understand the interactions of widely separated vortices, a convenient mathematical approach is to study the inviscid limit of the solution of the 2D Navier-Stokes equation when the initial data is a superposition of point vortices. This can be done by constructing a precise approximate solution which takes into account the deformation of the vortex cores due to mutual interactions.

Files for download:

Lecture slides (all four lectures in one file):

K.R. Rajagopal
Department of Mechanical Engineering
Texas A&M University
College Station, TX, 77843-3123
USA
email: krajagopal (at) tamu.edu
home: http://www2.mengr.tamu.edu/FacultyProfiles/facultyinformation.asp?LastName=krajagopal
Thermodynamics of Rate Type Viscoelastic Fluid Models

Abstract:
I will discuss the thermodynamic development of rate type viscoelastic models from two different perspectives, using the Helmholtz potential based on the deformation gradient and the rate of entropy production, and the Gibbs potential based on the stress and the rate of entropy production. These two methods are not equivalent and one cannot always be obtained from the other by using a Legendre transformation. Also, it is not even possible for certain classes of materials to define a Helmholtz potential for bodies belonging to such classes, and for certain other classes to define a Gibbs potential for bodies belonging to such classes. The Helmholtz potential formulation has been shown to be capable of modeling generalizations of the Maxwell, Oldroyd-B, Burgers model as well as models that can be cast within the context of the conformation tensor. These models can also describe the evolution of the anisotropy of such materials during the deformation process. The Gibbs potential formulation is particularly well suited to the development of models wherein the material moduli that characterize the body are dependent on the invariants of the stress.
Files for download:

Lecture 1:       Lecture 2:       Lecture 3:       Lecture 4:

Rolf Rannacher
Ruprecht-Karls-Universität Heidelberg
Institut für Angewandte Mathematik
Im Neuenheimer Feld 293
69120 Heidelberg
Germany
email: rannacher (at) iwr.uni-heidelberg.de
home: http://numerik.iwr.uni-heidelberg.de/~rannache/
Numerical simulation of viscous flow: discretization, optimization and stability

Abstract:

Numerical computation of incompressible viscous flow
In this first lecture, we discuss the Galerkin finite element method for the discretization of the Navier-Stokes equations. Particular emphasis is put on the aspects pressure stabilization and truncation to bounded domains.
Goal-oriented adaptivity
In this second lecture, we introduce the concept underlying the DWR (Dual Weighted Residual) method for goal-oriented residual-based adaptivity in solving the Navier-Stokes equations. This approach is presented for stationary as well as nonstationary situations.
Optimal flow control
In this third lecture, we discuss the use of the DWR method for adaptive discretization in flow control and parameter estimation.
Numerical stability analysis
In this fourth lecture, we consider the numerical stability analysis of stationary flows employing the concepts of linearized stability and pseudo-spectra.

Files for download:

Lecture 1:       Lecture 2:       Lecture 3:       Lecture 4:

David Silvester
School of Mathematics
University of Manchester
United Kingdom
email: d.silvester (at) manchester.ac.uk
home: http://www.maths.manchester.ac.uk/djs/
Finite Elements and Fast Solvers for Incompressible Flow Problems

Abstract:
Finite element approximation methods are widely used in scientific and engineering computations. The finite element method is also attractive from a mathematical perspective because of its rigorous underpinning. The short course will concentrate on incompressible flow problems and will develop two important aspects: the theory of a posteriori error estimation; and the design of fast iterative solvers. The following topics will be covered in the lectures:

Saddle-point problems. Inf-sup stability. The Stokes equations. A priori and a posteriori error estimation for mixed approximation methods. Properties of the discretized system. Multigrid preconditioned MINRES.
The Navier-Stokes equations for steady flow. Mixed approximation. Picard and Newton linearization methods. Properties of the discretized system.
Adaptive timestepping. Fully implicit solvers for unsteady flow problems.
Fast solvers for buoyancy driven flow problems.
In terms of linear algebra our emphasis will be on optimal methods where the work (and cpu time) associated with solution process is proportional to the dimension of the discretized system. At the heart of such optimal complexity methods are algebraic or geometric multigrid cycles applied as preconditioners for Krylov subspace methods.
Files for download:

IFISS - Installation and Software Guide:       Computational exercises:

Lecture 1:       Lecture 2:       Lecture 3:       Lecture 4: