Příklady k procvičení:
Je dána krychle \(ABCDEFGH\), \(|AB| = 4\mbox{ cm}\). Určete vzdálenost přímky \(S_{DH}F\) od roviny \(AS_{BF}D\).
Znázornění situace
Analytické řešení
Zadanou krychli jsem vhodně umístili do soustavy souřadnic:
K řešení využijeme rovnoběžník \(DS_{BF}FS_{DH}\), jehož výška odpovídá vzdálenosti přímky \(S_{DH}F\) od roviny \(AS_{BF}D\). Patu výšky z bodu \(S_{BF}\) označíme \(P\).
Obsah rovnoběžníku vypočítáme pomocí vektorového součinu vektorů \(\overrightarrow{S_{BF}D}=(-4;4;-2)\) a \(\overrightarrow{S_{BF}F}=(0;0;2)\):
\[\begin{eqnarray*}S &=& |\overrightarrow{S_{BF}D}\times\overrightarrow{S_{BF}F}|\\
&=&\bigl|(4\cdot 2-(-2)\cdot 0;(-2)\cdot 0-(-4)\cdot 2;(-4)\cdot 0-4\cdot 2)\bigr|\\
&=&|(8;8;0)|\\
&=&8\sqrt{2}\end{eqnarray*}\] Výšku rovnoběžníku získame vydělením obsahu délkou jeho základny:
\[|PS_{BF}|=\frac{S}{|S_{BF}D|}=\frac{8\sqrt{2}}{\sqrt{(-4)^2+4^2+(-2)^2}}=\frac{8\sqrt{2}}{\sqrt{16+16+4}}=\frac{8\sqrt{2}}{\sqrt{36}}=\frac{8\sqrt{2}}{6}=\frac{4\sqrt{2}}{3}\doteq 1,89\mbox{ cm.}\]
Syntetické početní řešení
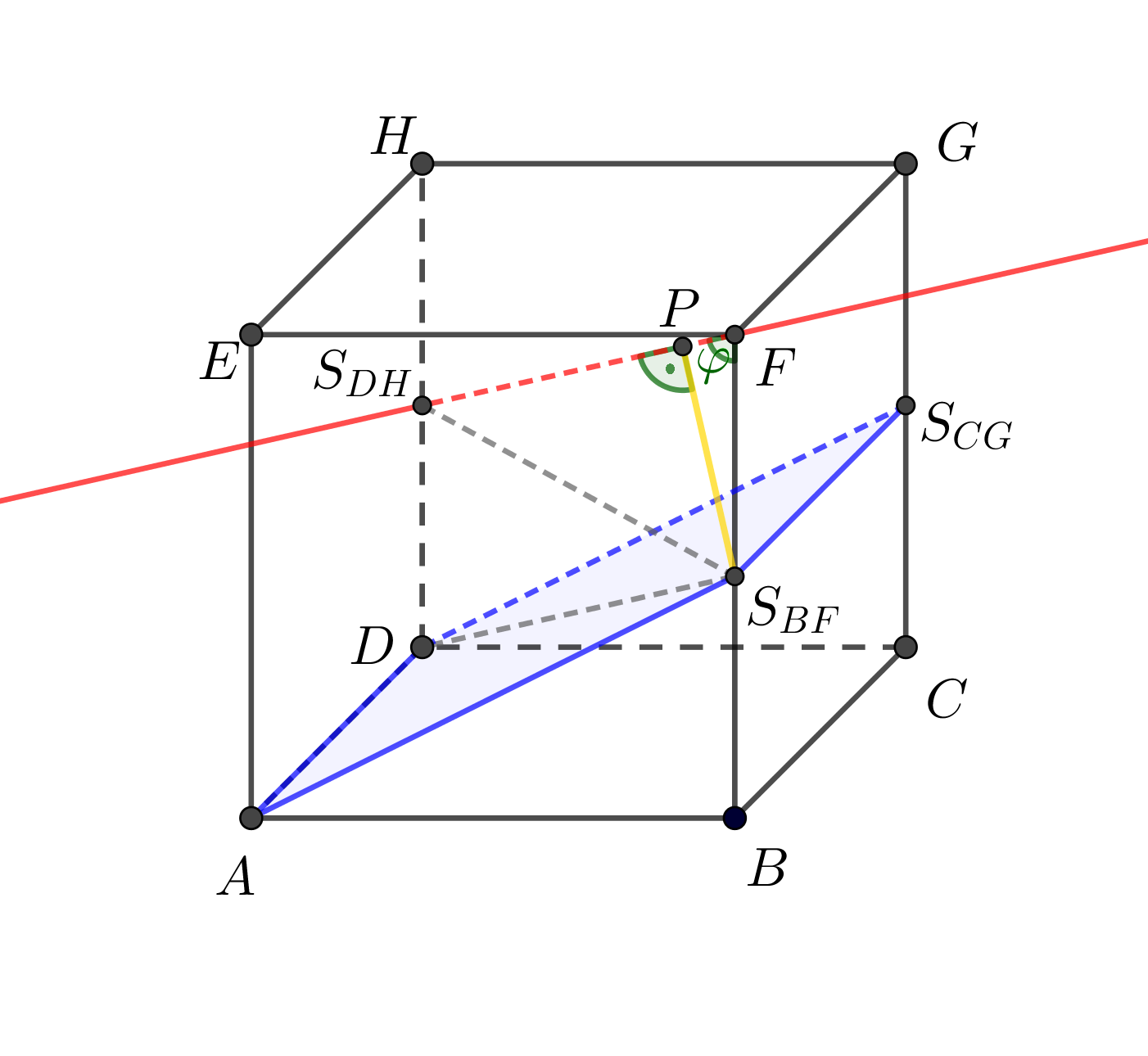
V řešení budeme pracovat s trojúhelníkem \(S_{DH}S_{BF}F\). Abychom mohli určit velikost úsečky \(PS_{BF}\) (bod \(P\) je patou výšky vedené z bodu \(S_{BF}\) trojúhelníku \(S_{DH}S_{BF}F\)), musíme znát velikost úhlu \(S_{DH}FS_{BF}\) (označíme jej \(\varphi\)). K výpočtu využijeme goniometrickou funkci tangens v trojúhelníku \(S_{DH}S_{BF}F\):
\[\tan\varphi=\frac{|S_{DH}S_{BF}|}{|S_{BF}F|}=\frac{4\sqrt{2}}{2}=2\sqrt{2}\Rightarrow\varphi\doteq 70^\circ 32^{'}\] Nyní pomocí funkce sinus získáme velikost úsečky \(PS_{BF}\):
\[\sin\varphi=\frac{|PS_{BF}|}{|S_{BF}F|}\Rightarrow |PS_{BF}|=|S_{BF}F|\cdot\sin\varphi=2\sin(70^\circ 32^{'})\doteq 1,89\mbox{ cm.}\]
Syntetické konstrukční řešení
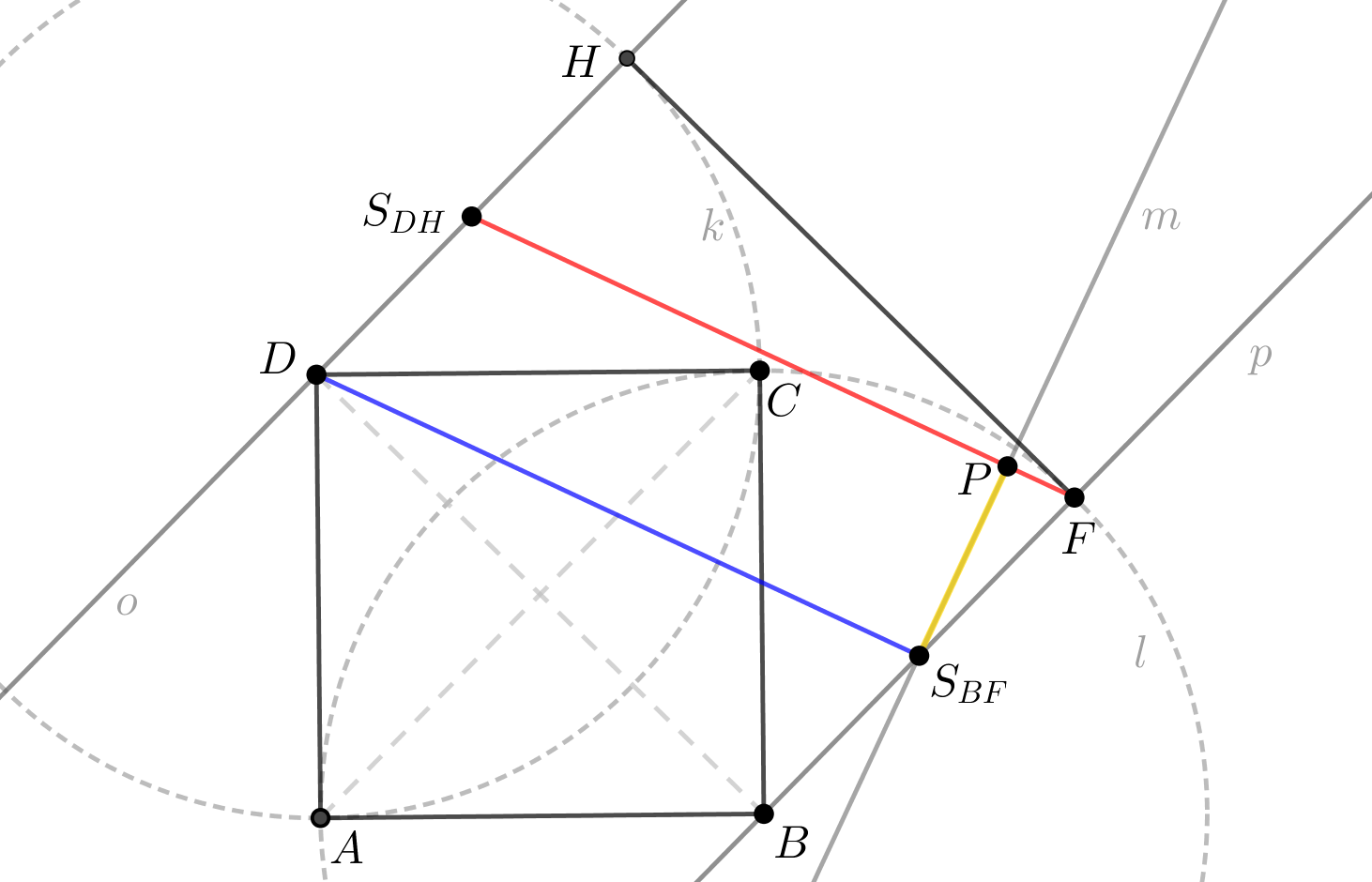
Zápis konstrukce:
\(\mbox{1) čtverec } ABCD; |AB|=4 \mbox{ cm}\)
\(\mbox{2) } \leftrightarrow o; o\perp \overline{DB} \wedge D\in o\)
\(\mbox{3) } \leftrightarrow p; p\perp \overline{DB} \wedge B\in p\)
\(\mbox{4) } k; k(D,|AB|)\)
\(\mbox{5) } l; l(B,|AB|)\)
\(\mbox{6) } H; H\in o\cap k \)
\(\mbox{7) } F; F\in p\cap l \wedge F\in\longmapsto BDH\)
\(\mbox{8) } S_{DH}; S_{DH}\mbox{ je středem úsečky } DH\)
\(\mbox{9) } S_{BF}; S_{BF}\mbox{ je středem úsečky } BF\)
\(\mbox{10) } \leftrightarrow m; m\perp \overline{S_{DH}F} \wedge S_{BF}\in m\)
\(\mbox{11) } P; m\cap\overline{S_{DH}F} = \{P\} \)
Provedením konstrukce jsme získali vzdálenost bodů \(P\) a \(S_{BF}\), čímž jsme sestrojili vzdálenost přímky \(S_{DH}F\) od roviny \(AS_{BF}D\).
Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 4\mbox{ cm}\). Určete vzdálenost přímky \(S_{DV}S_{AB}\) od roviny \(BCV\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Přímka \(S_{DV}S_{AB}\) je rovnoběžná s rovinou \(BCV\). Vezměme tedy libovolný bod přímy \(S_{DV}S_{AB}\), například bod \(S_{DV}\), a určeme jeho vzdálenost od roviny \(BCV\) (označme ji \(\varrho\)).
Vzdálenost bodu od roviny můžeme určit pomocí vztahu:
\[d(S_{DV},\varrho)=\frac{|ax_{S_{DV}}+by_{S_{DV}}+cz_{S_{DV}}+d|}{\sqrt{a^2+b^2+c^2}}\] Rovina \(\varrho\) má obecnou rovnici \(ax+by+cz+d=0\) a \(S_{DV}=[x_{S_{DV}};y_{S_{DV}};z_{S_{DV}}]=[1;3;2]\).
Potřebujeme tedy určit normálový vektor roviny.
Normálový vektor lze určit pomocí dvou směrových vektorů této roviny, například:
\[\overrightarrow{CV}=(-2;-2;4),\quad\overrightarrow{CB}=(0;-4;0)\] Určeme normálový vektor roviny \(\varrho\):
\[\begin{eqnarray*}\overrightarrow{n_\varrho}&=&\overrightarrow{CV}\times\overrightarrow{CB}\\
&=&((-2)\cdot 0-4\cdot (-4);4\cdot 0-(-2)\cdot 0;(-2)\cdot (-4)-(-2)\cdot 0)\\
&=&(16;0;8)\sim(2;0;1)\end{eqnarray*}\] Do rovnice \(2x+0y+z+d\) dosadíme libovolný z bodů \(B, C, V\) a dopočítáme \(d=-8\).
Rovnice roviny má tedy tvar:
\[2x+z-8=0\] Nyní můžeme dosadit do výše uvedeného vztahu pro výpočet vzdalenosti bodu od roviny:
\[d(S_{DV},\varrho)=\frac{|2\cdot 1+0\cdot 3+1\cdot 2-8|}{\sqrt{2^2+1^2}}=\frac{|-4|}{\sqrt{5}}=\frac{4\sqrt{5}}{5}\doteq 1,79\mbox{ cm.}\]
Syntetické početní řešení
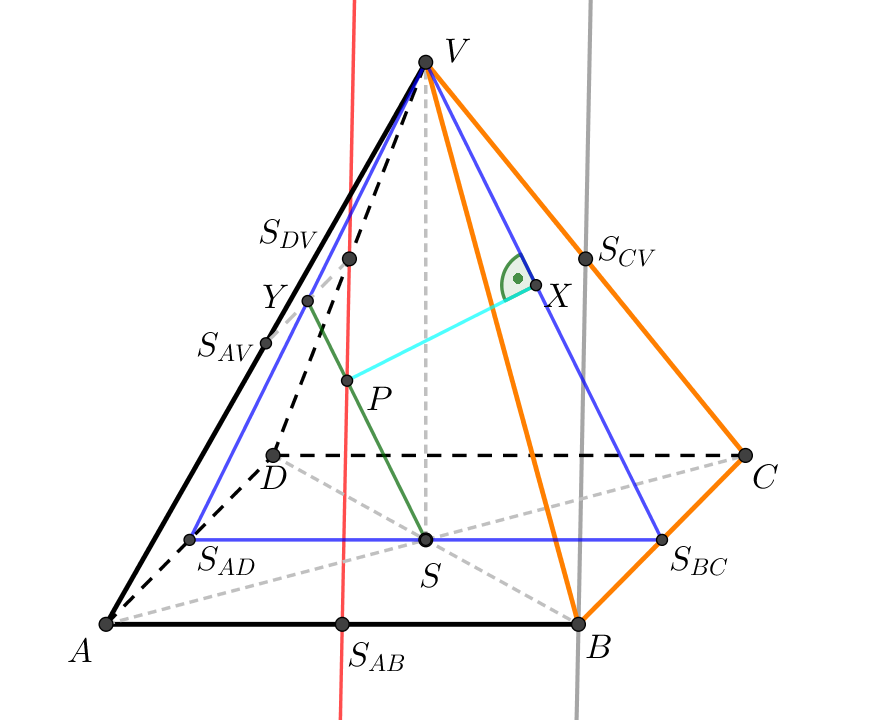
Přímka \(S_{DV}S_{AB}\) je rovnoběžná s přímkou \(S_{CV}B\) (jde o protější strany rovnoběžníka).
Přímka \(S_{DV}S_{AB}\) je tedy rovnoběžná s rovinou \(BCV\) a její vzdálenost od této roviny vypočítáme jako
vzdálenost libovolného bodu přímky \(S_{DV}S_{AB}\) od roviny \(BCV\).
Uvažujme bod \(P\) přímky \(S_{DV}S_{AB}\), který je jejím průsečíkem s rovinou \(S_{AD}S_{BC}V\).
Hledanou vzdáleností je potom délka úsečky \(PX\), kde \(X\) je patou kolmice vedené z bodu \(P\) na úsečku \(S_{BC}V\). Úsečka \(SY\) je kolmým průmětem úsečky \(S_{AB}S_{DV}\) do roviny \(S_{AD}S_{BC}V\).
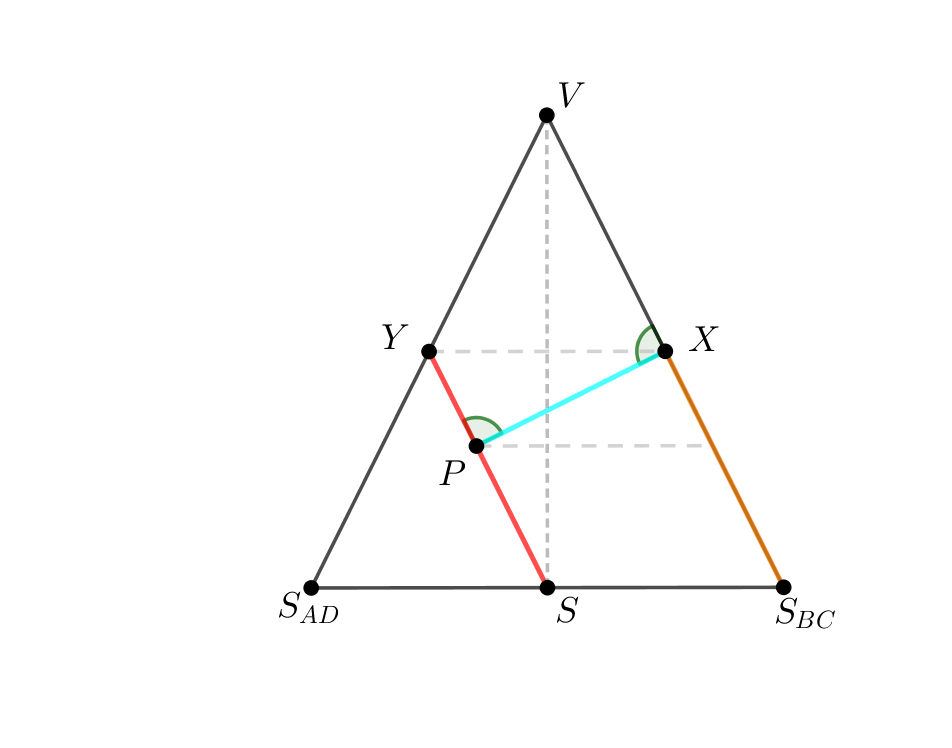Trojúhelníky \(SVS_{AD}\) a \(PXY\) jsou podobné podle věty \(uu\), neboť \(SY\) a \(XY\) jsou střední příčky trojúhelníku \(S_{AD}S_{BC}V\), a tedy \(|\angle XYP|=|\angle YSS_{AD}|=|\angle VS_{BC}S_{AD}|=|VS_{AD}S|\) a
\(|\angle XPY|=90^\circ\).
Dále potřebujeme délku úsečky \(S_{AD}V\). Zjistíme ji například z trojúhelníku \(S_{AD}SV\):
\[|S_{AD}V|=\sqrt{|S_{AD}S|^2+|SV|^2}=\sqrt{2^2+4^2}=\sqrt{4+16}=\sqrt{20}=2\sqrt{5}\] Nyní můžeme využít výše uvedené podobnosti trojúhelníků \(SVS_{AD}\) a \(PXY\):
\[\frac{|PX|}{|XY|}=\frac{|SV|}{|VS_{AD}|}\] \[|PX|=\frac{|SV|}{|VS_{AD}|}|XY|\] \[|PX|=\frac{4}{2\sqrt{5}}\cdot 2\] \[|PX|=\frac{4}{\sqrt{5}}\doteq 1,79\mbox{ cm}\]
Syntetické konstrukční řešení
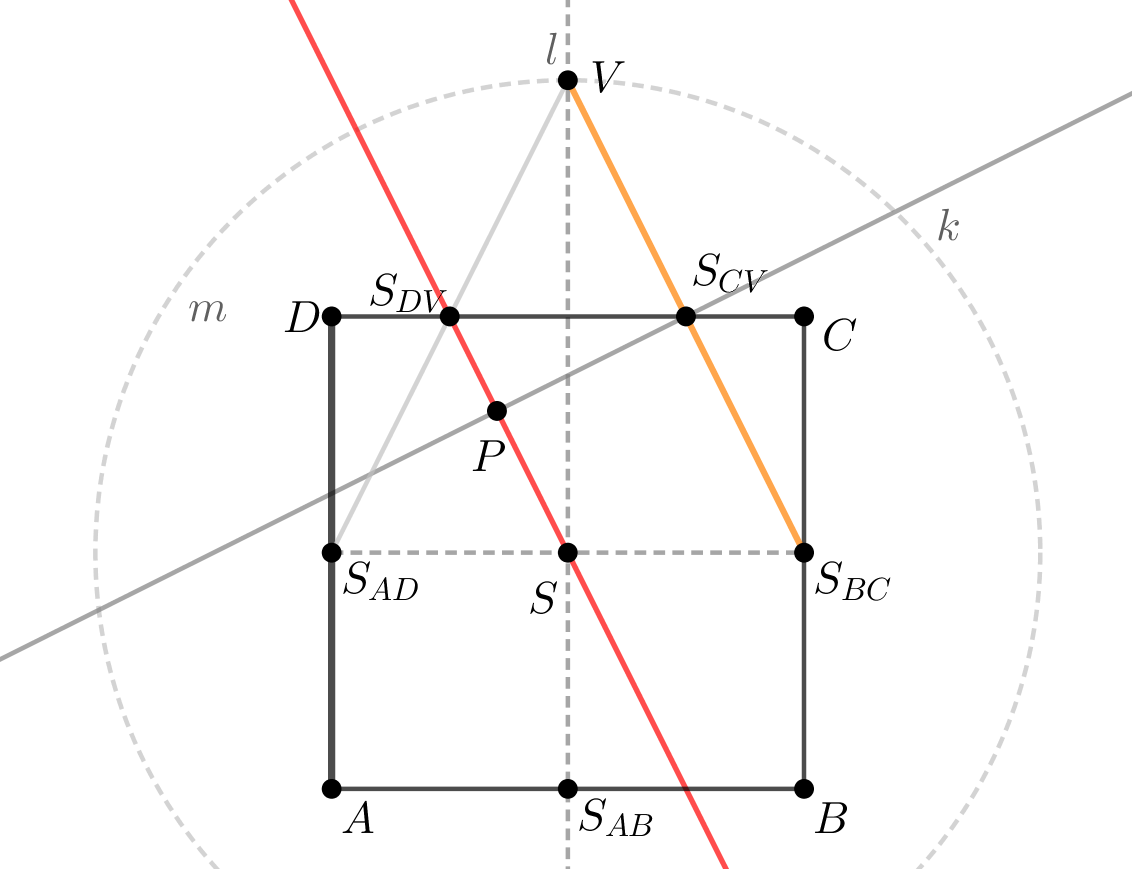
Zápis konstrukce:
\(\mbox{1) } \mbox{čtverec } ABCD; |AB|=4 \mbox{ cm}\)
\(\mbox{2) } S; S\mbox{ je středem }\overline{AC}\)
\(\mbox{3) } l; l\perp AB \wedge S\in l \)
\(\mbox{4) } m; m(S,4\mbox{ cm})\)
\(\mbox{5) } V; V\in l\cap m\)
\(\mbox{6) } S_{AD}; S_{AD}\mbox{ je středem úsečky} \overline{AD}\)
\(\mbox{7) } S_{BC}; S_{BC}\mbox{ je středem úsečky} \overline{BC}\)
\(\mbox{8) } S_{DV}; S_{DV}\mbox{ je středem úsečky} \overline{S_{AD}V}\)
\(\mbox{9) } S_{CV}; S_{CV}\mbox{ je středem úsečky} \overline{S_{BC}V}\)
\(\mbox{10) } k; k\perp\overline{S_{DV}S}\wedge S_{CV}\in k\)
\(\mbox{11) } P; \overline{S_{DV}S}\cap k = \{P\} \)
Provedením konstrukce jsme získali vzdálenost bodů \(S_{CV}\), \(P\), čímž jsme sestrojili vzdálenost přímky \(S_{DV}S_{AB}\) od roviny \(BCV\).
