Příklady k procvičení:
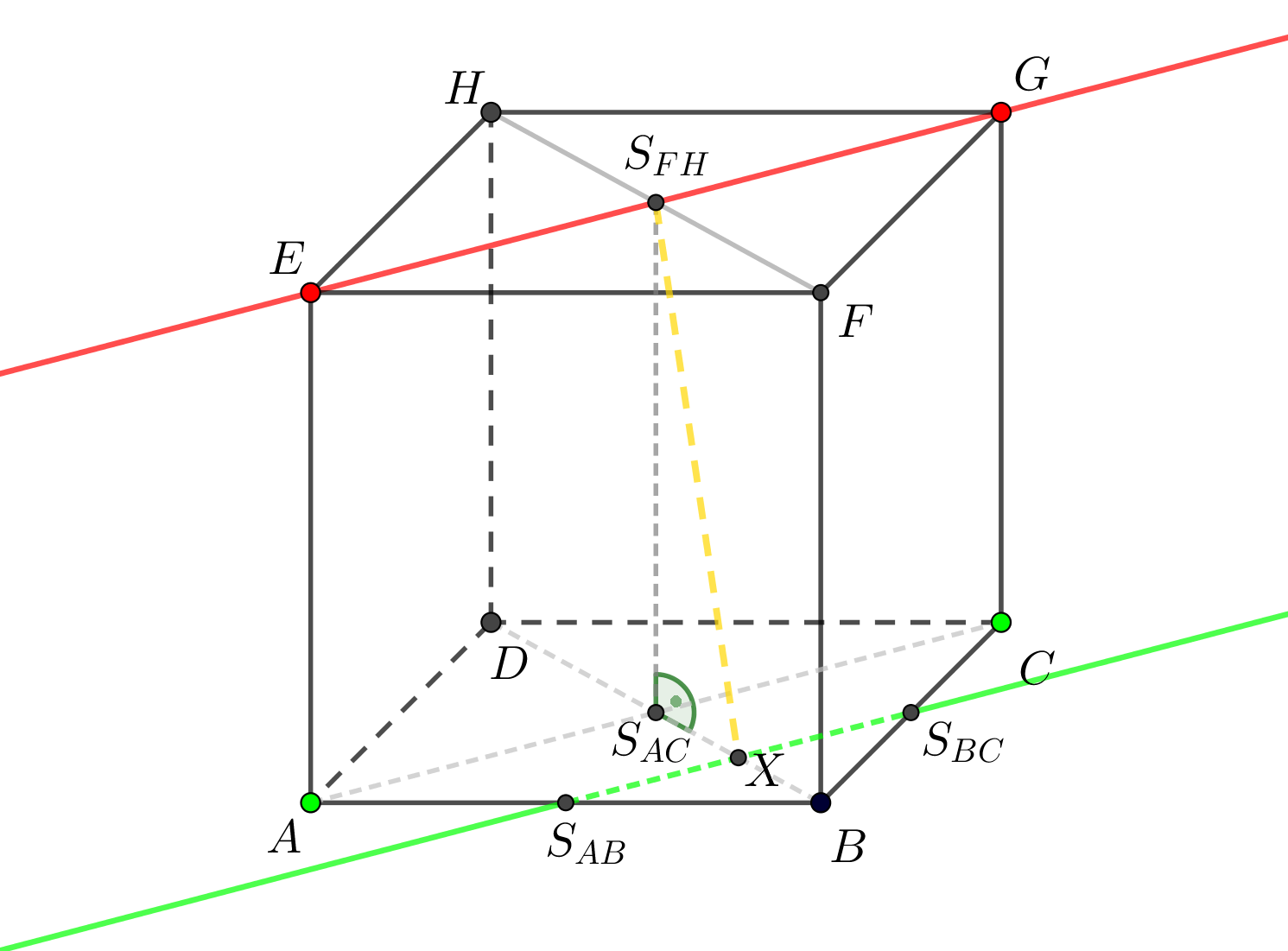
Je dána krychle ABCDEFGH, |AB| = 4\mbox{ cm}. Určete vzdálenost přímky EG od přímky S_{AB}S_{BC}.
Znázornění situace
Analytické řešení
Zadanou krychli jsem vhodně umístili do soustavy souřadnic:
K řešení využijeme doplnění na rovnoběžník ES_{AB}NG (viz obrázek), jehož výška (PS_{AB}) je rovna hledané vzdálenosti
přímek EG, S_{AB}S_{BC}.
Výšku rovnoběžníku ES_{AB}NG odvodíme z jeho obsahu. Obsah rovnoběžník získáme vektorovým součinem vektorů \overrightarrow{EG}=(4;4;0), ES_{AB}=(2;0;-4).
Výšku rovnoběžníku ES_{AB}NG odvodíme z jeho obsahu. Obsah rovnoběžník získáme vektorovým součinem vektorů \overrightarrow{EG}=(4;4;0), ES_{AB}=(2;0;-4).
\begin{eqnarray*}S&=&|\overrightarrow{EG}\times\overrightarrow{ES_{AB}}|\\
&=&\bigl|(4\cdot (-4)-0\cdot 0;0\cdot 2-4\cdot (-4);4\cdot 0-4\cdot 2)\bigr|\\
&=&|(-16;16;-8)|\\
&=&24\end{eqnarray*}
Nyní již můžeme vypočítat hledanou výšku rovnoběžníku ES_{AB}NG:|PS_{AB}|=\frac{S}{|EG|}=\frac{24}{\sqrt{4^2+4^2+0^2}}=\frac{24}{\sqrt{32}}=\frac{24}{4\sqrt{2}}=\frac{6}{\sqrt{2}}=3\sqrt{2}\doteq 4,24\mbox{ cm}
Syntetické početní řešení
Můžeme nahlédnout, že průsečík X přímky S_{AB}S_{BC} s úsečkou BD je středem úsečky S_{AC}B. Vzdálenost bodů S_{FH}X lze tedy vypočítat pomocí Pýthagorovy věty v trojúhelníku S_{FH}S_{AC}X.
|S_{FH}X|=\sqrt{|S_{AC}X|^2+|S_{AC}S_{FH}|^2}
|S_{FH}X|=\sqrt{\Biggl(\frac{1}{4}|AC|\Biggr)^2+|S_{AC}S_{FH}|^2}=\sqrt{\Bigl(\sqrt{2}\Bigr)^2+4^2}=\sqrt{2+16}=\sqrt{18}\doteq 4,24\mbox{ cm}
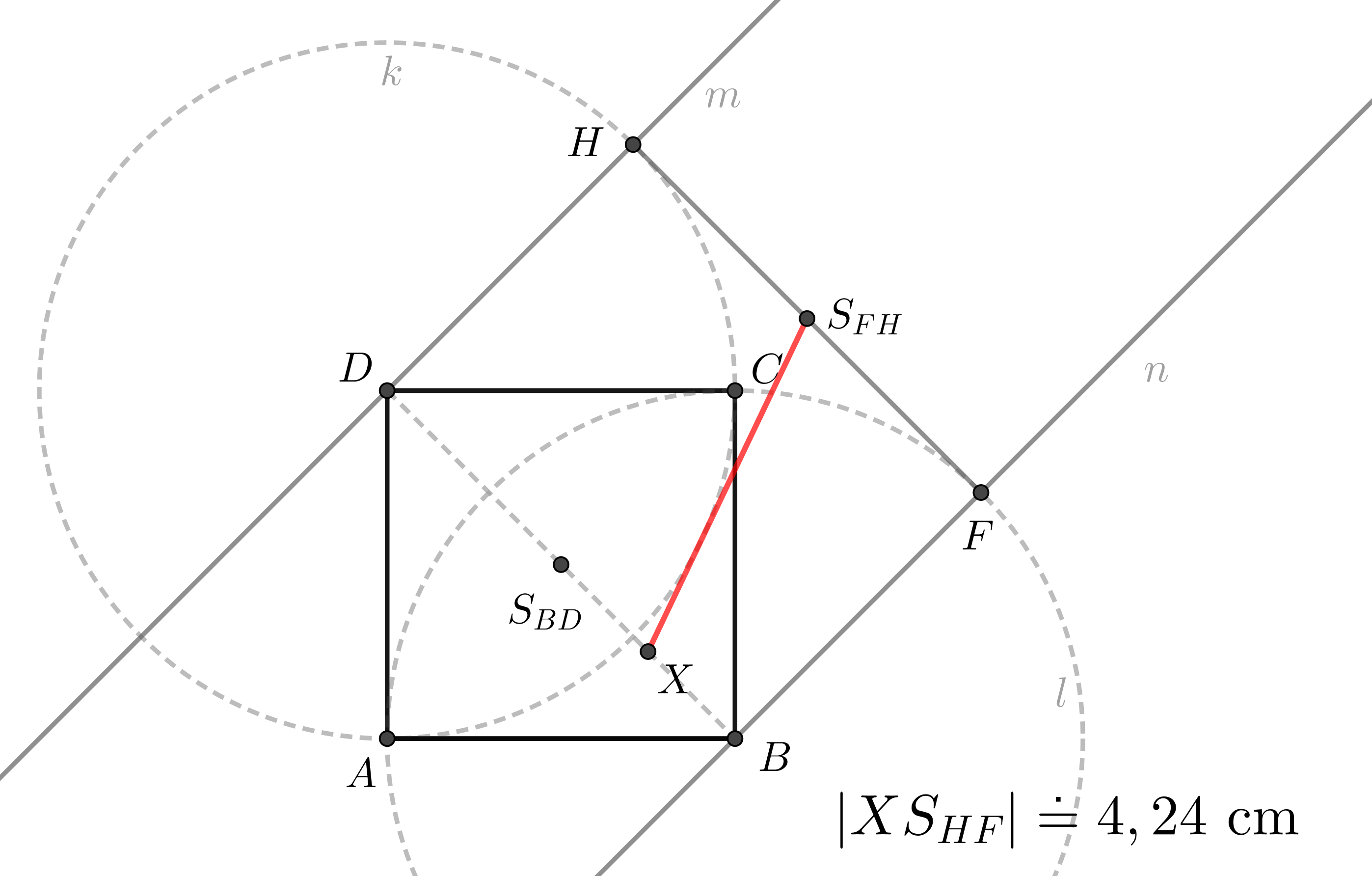
Syntetické konstrukční řešení
Zápis konstrukce:
\mbox{1) čtverec } ABCD; |AB|=4 \mbox{ cm}
\mbox{2) } \leftrightarrow n; n\perp \overline{DB} \wedge B\in n
\mbox{3) } \leftrightarrow m; m\perp \overline{DB} \wedge D\in m
\mbox{4) } k; k(D,|AB|)
\mbox{5) } l; l(B,|AB|)
\mbox{6) } H; H\in k\cap m
\mbox{7) } F; F\in l\cap n \wedge F\in\longmapsto BDH
\mbox{8) } S_{FH}; S_{FH}\in FH, |FS_{FH}|=|S_{FH}H|
\mbox{9) } S_{BD}; S_{BD}\in BD\wedge |BS_{BD}|=|S_{BD}D|
\mbox{10) } X; X\in \overline{S_{BD}B}\wedge |S_{BD}X|=|XB|
Provedením konstrukce jsme získali vzdálenost bodů X a S_{FH}, čímž jsme sestrojili vzdálenost přímek EG, S_{AB}S_{BC}.\mbox{2) } \leftrightarrow n; n\perp \overline{DB} \wedge B\in n
\mbox{3) } \leftrightarrow m; m\perp \overline{DB} \wedge D\in m
\mbox{4) } k; k(D,|AB|)
\mbox{5) } l; l(B,|AB|)
\mbox{6) } H; H\in k\cap m
\mbox{7) } F; F\in l\cap n \wedge F\in\longmapsto BDH
\mbox{8) } S_{FH}; S_{FH}\in FH, |FS_{FH}|=|S_{FH}H|
\mbox{9) } S_{BD}; S_{BD}\in BD\wedge |BS_{BD}|=|S_{BD}D|
\mbox{10) } X; X\in \overline{S_{BD}B}\wedge |S_{BD}X|=|XB|
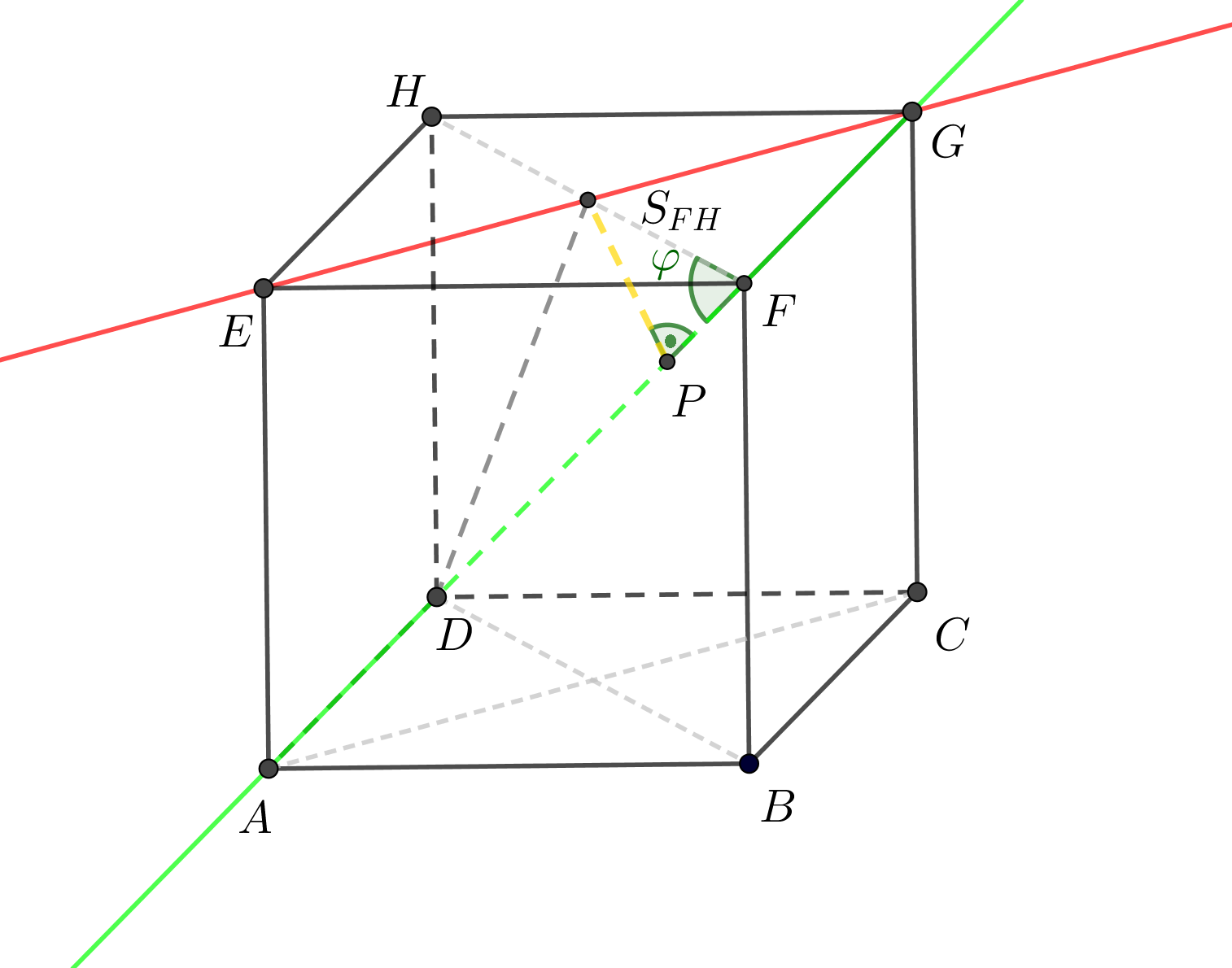
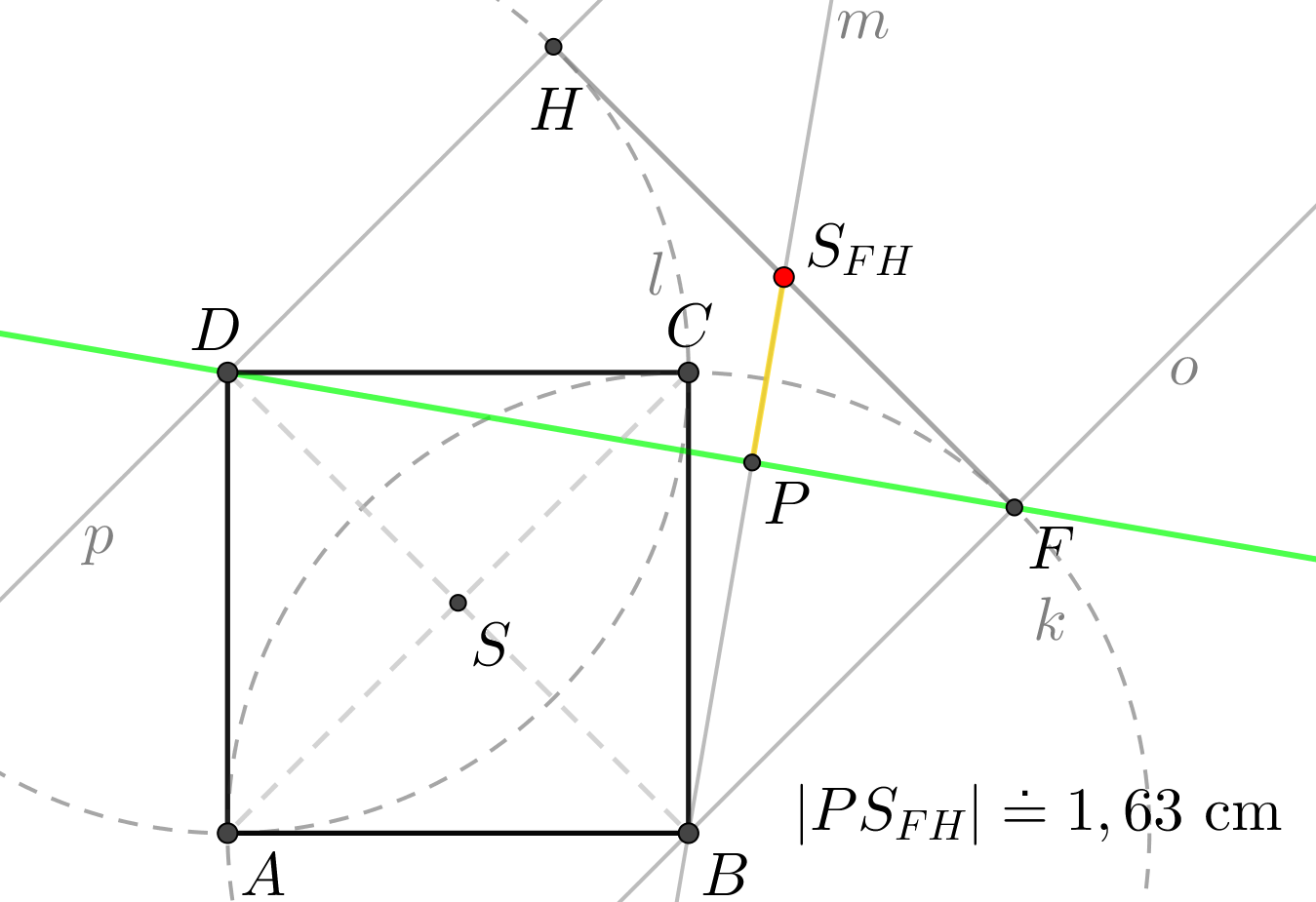
Je dána krychle ABCDEFGH, |AB| = 4\mbox{ cm}. Určete vzdálenost přímky EG od přímky DF.
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Parametrické vyjádření přímky EG:
\leftrightarrow EG:\quad x=4t,\quad y=4t,\quad z=4,\quad t\in\mathbb{R}
Parametrické vyjádření přímky DF:\leftrightarrow DF:\quad x=4s,\quad y=4-4s,\quad z=4s,\quad s\in\mathbb{R}
Bod P náleží přímce DF. Jeho souřadnice jsou tedy:P=[4s;4-4s;4s]
K řešení využijeme kolmost vektorů - \overrightarrow{EG}\perp\overrightarrow{S_{FH}P} a \overrightarrow{DF}\perp\overrightarrow{S_{FH}P}:
\overrightarrow{EG}\cdot\overrightarrow{S_{FH}P}=0\wedge\overrightarrow{DF}\cdot\overrightarrow{S_{FH}P}=0
Pro vektory \overrightarrow{EG}, \overrightarrow{S_{FH}P} a \overrightarrow{DF} platí:
\overrightarrow{EG}=(4;4;0)\quad\overrightarrow{DF}=(4;-4;4)\quad\overrightarrow{S_{FH}P}=(4s-2;4-4s-2;4s-4)
Nyní vypočítejme parametr s\in\mathbb{R} pomocí soustavy rovnic:\overrightarrow{EG}\cdot\overrightarrow{S_{FH}P}=0
\underline{\overrightarrow{DF}\cdot\overrightarrow{S_{FH}P}=0}
(4;4;0)\cdot(4s-2;4-4s-2;4s-4)=0
\underline{(4;-4;4)\cdot(4s-2;4-4s-2;4s-4)=0}
16s-8+16-16s-8=0
\underline{16s-8-16+16s+8+16s-16=0}
0s=0 \Rightarrow s\in\mathbb{R}
48s=32 \Rightarrow s=\frac{2}{3}
Bod P=[\frac{8}{3};\frac{4}{3};\frac{8}{3}], velikost vektoru \overrightarrow{S_{FH}P} je tedy rovna:
|\overrightarrow{S_{FH}P}|=\Biggl|\biggl(\frac{2}{3};-\frac{2}{3};-\frac{4}{3}\biggr)\Biggr|=\sqrt{\frac{4}{9}+\frac{4}{9}+\frac{16}{9}}=\sqrt{\frac{24}{9}}=\frac{2\sqrt{6}}{3}\doteq 1,63\mbox{ cm}
Syntetické početní řešení
Během řešení se budeme pohybovat v trojúhelníku DFS_{FH}. Nejprve vypočteme velikost úhlu S_{FH}FD (označíme \varphi),
jenž využijeme během výpočtu délky úsečky S_{FH}P v trojúhelníku S_{FH}PF.
Velikost úhlu \varphi určíme pomocí kosinové věty:
Velikost úhlu \varphi určíme pomocí kosinové věty:
\cos\varphi=\frac{|DS_{FH}|^2-|S_{FH}F|^2-|DF|^2}{-2|DF||S_{FH}F|}
Platí:|DS_{FH}|=\sqrt{|DH|^2+\biggl(\frac{1}{2}|AB|\sqrt{2}\biggr)^2}=\sqrt{4^2+(2\sqrt{2})^2}=\sqrt{24}=2\sqrt{6}
|S_{FH}F|=\frac{1}{2}|AB|\sqrt{2}=\frac{1}{2}\cdot 4\sqrt{2}=2\sqrt{2}
|DF|=\sqrt{|DB|^2+|BF|^2}=\sqrt{\bigl(|AB|\sqrt{2}\bigr)^2+|AB|^2}=\sqrt{(4\sqrt{2})^2+4^2}=\sqrt{3\cdot 16}=4\sqrt{3}
Dosaďme do kosinové věty:\cos\varphi=\frac{\bigl(2\sqrt{6}\bigr)^2-\bigl(2\sqrt{2}\bigr)^2-\bigl(4\sqrt{3}\bigr)^2}{-2\cdot 4\sqrt{3}\cdot 2\sqrt{2}}=\frac{-32}{-16\sqrt{6}}=\frac{2}{\sqrt{6}}=\frac{\sqrt{6}}{3}\Rightarrow \varphi\doteq 35^\circ 15^{'}
Užitím goniometrické funkce sinus v trojúhelníku S_{FH}PF získáme |S_{FH}P|:\sin\varphi=\frac{|S_{FH}P|}{|S_{FH}F|}\Rightarrow |S_{FH}P|=|S_{FH}F|\cdot\sin\varphi =2\sqrt{2}\cdot\sin(35^\circ 15^{'})\doteq 1,63\mbox{ cm}
Syntetické konstrukční řešení
Zápis konstrukce:
\mbox{1) čtverec } ABCD; |AB|=4 \mbox{ cm}
\mbox{2) } \leftrightarrow o; o\perp \overline{DB} \wedge B\in o
\mbox{3) } \leftrightarrow p; p\perp \overline{DB} \wedge D\in p
\mbox{4) } k; k(B,|AB|)
\mbox{5) } l; l(D,|AB|)
\mbox{6) } F; F\in k\cap o
\mbox{7) } H; H\in l\cap p \wedge H\in \longmapsto BDF
\mbox{8) } S_{FH};S_{FH}\in FH\wedge |FS_{FH}|=|S_{FH}H|
\mbox{9) } \leftrightarrow m; m\perp \overline{DF} \wedge S_{FH}\in m
\mbox{10) } P; m\cap \overline{DF} = \{P\}
Provedením konstrukce jsme získali vzdálenost bodů P a S_{FH}, čímž jsme sestrojili vzdálenost přímek EG a DF.
\mbox{2) } \leftrightarrow o; o\perp \overline{DB} \wedge B\in o
\mbox{3) } \leftrightarrow p; p\perp \overline{DB} \wedge D\in p
\mbox{4) } k; k(B,|AB|)
\mbox{5) } l; l(D,|AB|)
\mbox{6) } F; F\in k\cap o
\mbox{7) } H; H\in l\cap p \wedge H\in \longmapsto BDF
\mbox{8) } S_{FH};S_{FH}\in FH\wedge |FS_{FH}|=|S_{FH}H|
\mbox{9) } \leftrightarrow m; m\perp \overline{DF} \wedge S_{FH}\in m
\mbox{10) } P; m\cap \overline{DF} = \{P\}
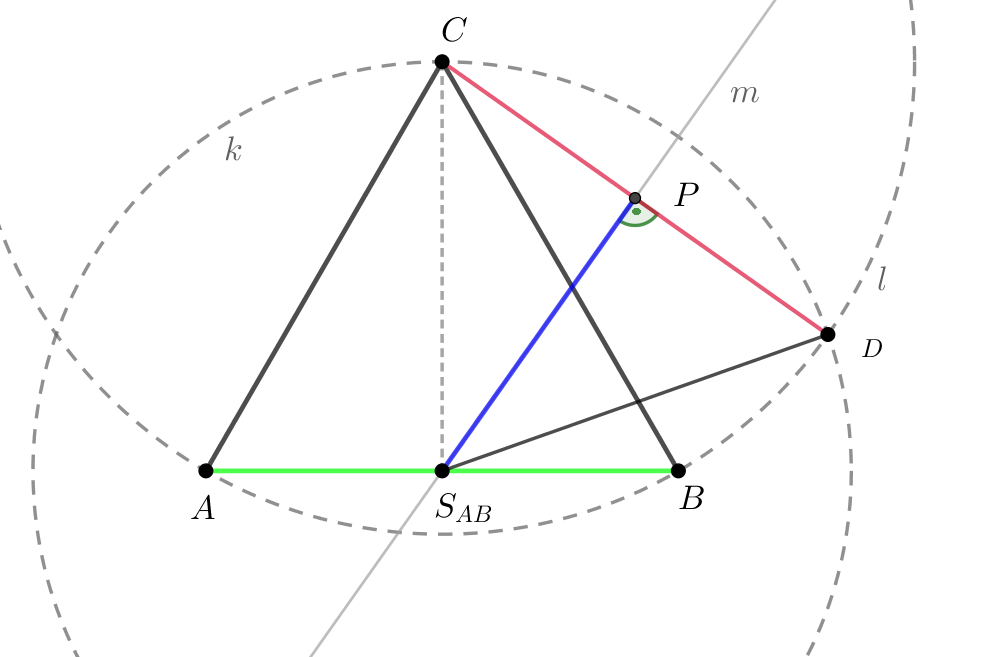
Je dán pravidelný čtyřstěn ABCD, |AB|=4\mbox{ cm}. Určete vzdálenost hran AB a DC.
Znázornění situace
Analytické řešení
Zadaný čtyřstěn jsme vhodně umístili do soustavy souřadnic:
X -ovou souřadnici bodu C jsme získali výpočtem výšky v rovnostranném trojúhelníku ABC.
Souřadnice bodu D jsme odvodili na základě souřadnic těžiště T trojúhelníku ABC a na základě pravoúhlého trojúhelníku TCD.
Určeme parametrická vyjádření přímek AB a CD:
K výpočtu vzdálenosti obou přímek využijeme kolmost vektorů \overrightarrow{AB}\perp\overrightarrow{S_{AB}P} a \overrightarrow{CD}\perp\overrightarrow{S_{AB}P} (S_{AB}P je kolmá příčka přímek AB, CD a P\in CD):
Souřadnice bodu D jsme odvodili na základě souřadnic těžiště T trojúhelníku ABC a na základě pravoúhlého trojúhelníku TCD.
Určeme parametrická vyjádření přímek AB a CD:
\leftrightarrow AB:\quad x=0,\quad y=4t,\quad z=0,\quad t\in\mathbb{R}
\leftrightarrow CD:\quad x=2\sqrt{3}+\biggl(\frac{2}{3}\sqrt{3}-2\sqrt{3}\biggr)s,\quad y=2,\quad z=4\sqrt{\frac{2}{3}}s,\quad s\in\mathbb{R}
Směrovým vektorem přímky AB je vektor \overrightarrow{AB}=(0;4;0) a směrovým vektorem přímky CD je vektor \overrightarrow{CD}=\Bigl(\frac{2}{3}\sqrt{3}-2\sqrt{3};0;4\sqrt{\frac{2}{3}}\Bigr).K výpočtu vzdálenosti obou přímek využijeme kolmost vektorů \overrightarrow{AB}\perp\overrightarrow{S_{AB}P} a \overrightarrow{CD}\perp\overrightarrow{S_{AB}P} (S_{AB}P je kolmá příčka přímek AB, CD a P\in CD):
\overrightarrow{AB}\cdot\overrightarrow{S_{AB}P}=0\wedge\overrightarrow{CD}\cdot\overrightarrow{S_{AB}P}=0
P=\Biggl[2\sqrt{3}+(\frac{2}{3}\sqrt{3}-2\sqrt{3})s;2;4\sqrt{\frac{2}{3}}s\Biggr]\wedge\overrightarrow{S_{AB}P}=\Biggl(2\sqrt{3}+\Biggl(\frac{2}{3}\sqrt{3}-2\sqrt{3}\Biggr)s;0;4\Biggr)
Můžeme nahlédnout, že řešením rovnice \overrightarrow{AB}\cdot\overrightarrow{S_{AB}P}=0 je s\in\mathbb{R}. Zkusme vypočítat druhou rovnici:\overrightarrow{CD}\cdot\overrightarrow{S_{AB}P}=0
\biggl(\frac{2}{3}\sqrt{3}-2\sqrt{3};0;4\sqrt{\frac{2}{3}}\Biggr)\cdot\Biggl(2\sqrt{3}+(\frac{2}{3}\sqrt{3}-2\sqrt{3})s;0;4\sqrt{\frac{2}{3}}\Biggr)=0
4-4\cdot 3+\Biggl(\frac{2}{3}\sqrt{3}-2\sqrt{3}\Biggr)^2s+16\cdot \frac{2}{3}s=0
\Biggl(\frac{4}{3}+12-2\cdot \frac{2}{3}\sqrt{3}\cdot 2\sqrt{3}\Biggr)s+\frac{32}{3}s=8
4s+36s-24s+32s=24
48s=24
s=\frac{1}{2}
Parametr s=\frac{1}{2} dosadíme do vektoru \overrightarrow{S_{AB}P}:\overrightarrow{S_{AB}P}=\Biggl(2\sqrt{3}+\Bigl(\frac{2}{3}\sqrt{3}-2\sqrt{3}\Bigr)\frac{1}{2};0;2\sqrt{\frac{2}{3}}\Biggr)
|\overrightarrow{S_{AB}P}|=\sqrt{\Biggl(2\sqrt{3}\frac{1}{3}\sqrt{3}-\sqrt{3}\Biggr)^2+\Biggl(2\sqrt{\frac{2}{3}}\Biggr)^2}
|\overrightarrow{S_{AB}P}|=\sqrt{\Biggl(\frac{4}{3}\sqrt{3}\Biggr)^2+\frac{8}{3}}=\sqrt{\frac{16}{9}\cdot 3+\frac{8}{3}}=\sqrt{\frac{24}{3}}=\sqrt{8}=2\sqrt{2}\doteq 2,83\mbox{ cm}
Syntetické početní řešení
Řezem čtyřstěnu rovinou kolmou k hraně AB a procházející hranou CD je rovnoramenný trojúhelník S_{AB}CD s rameny S_{AB}D, S_{AB}C.
Délky ramen S_{AB}C, S_{AB}D jsou rovny výšce v rovnostranném trojúhelníku ACB, tj. |S_{AB}C|=\frac{|AC|}{2}\sqrt{3}=2\sqrt{3}.
Vzdálenost hran AB a CD je rovna výšce v trojúhelníku S_{AB}CD k základně CD.
Výšku S_{AB}P v rovnoramenném trojúhelníku S_{AB}CD určíme z pravoúhlého trojúhelníku S_{AB}CP:
Výšku S_{AB}P v rovnoramenném trojúhelníku S_{AB}CD určíme z pravoúhlého trojúhelníku S_{AB}CP:
|S_{AB}P|=\sqrt{|S_{AB}C|^2-|CP|^2}=\sqrt{(2\sqrt{3})^2-2^2}=\sqrt{12-4}=\sqrt{8}=2\sqrt{2}\doteq 2,83\mbox{ cm}
Syntetické konstrukční řešení
Zápis konstrukce:
\mbox{1) } \mbox{rovnostranný trojúhelník } ABC; |AB|=4 \mbox{ cm}
\mbox{2) } S_{AB}; S_{AB}\mbox{ je střed strany }AB
\mbox{3) } \triangle S_{AB}DC; |CD|=4\mbox{ cm, }|S_{AB}D|=|S_{AB}C|
\mbox{4 } m; m\perp\overline{CD}\wedge S_{AB}\in m
\mbox{5) } P; m\cap \overline{CD} = \{P\}
Provedením konstrukce jsme získali vzdálenost bodů S_{AB}, P, čímž jsme sestrojili vzdálenost přímek AB a DC.
\mbox{2) } S_{AB}; S_{AB}\mbox{ je střed strany }AB
\mbox{3) } \triangle S_{AB}DC; |CD|=4\mbox{ cm, }|S_{AB}D|=|S_{AB}C|
\mbox{4 } m; m\perp\overline{CD}\wedge S_{AB}\in m
\mbox{5) } P; m\cap \overline{CD} = \{P\}
