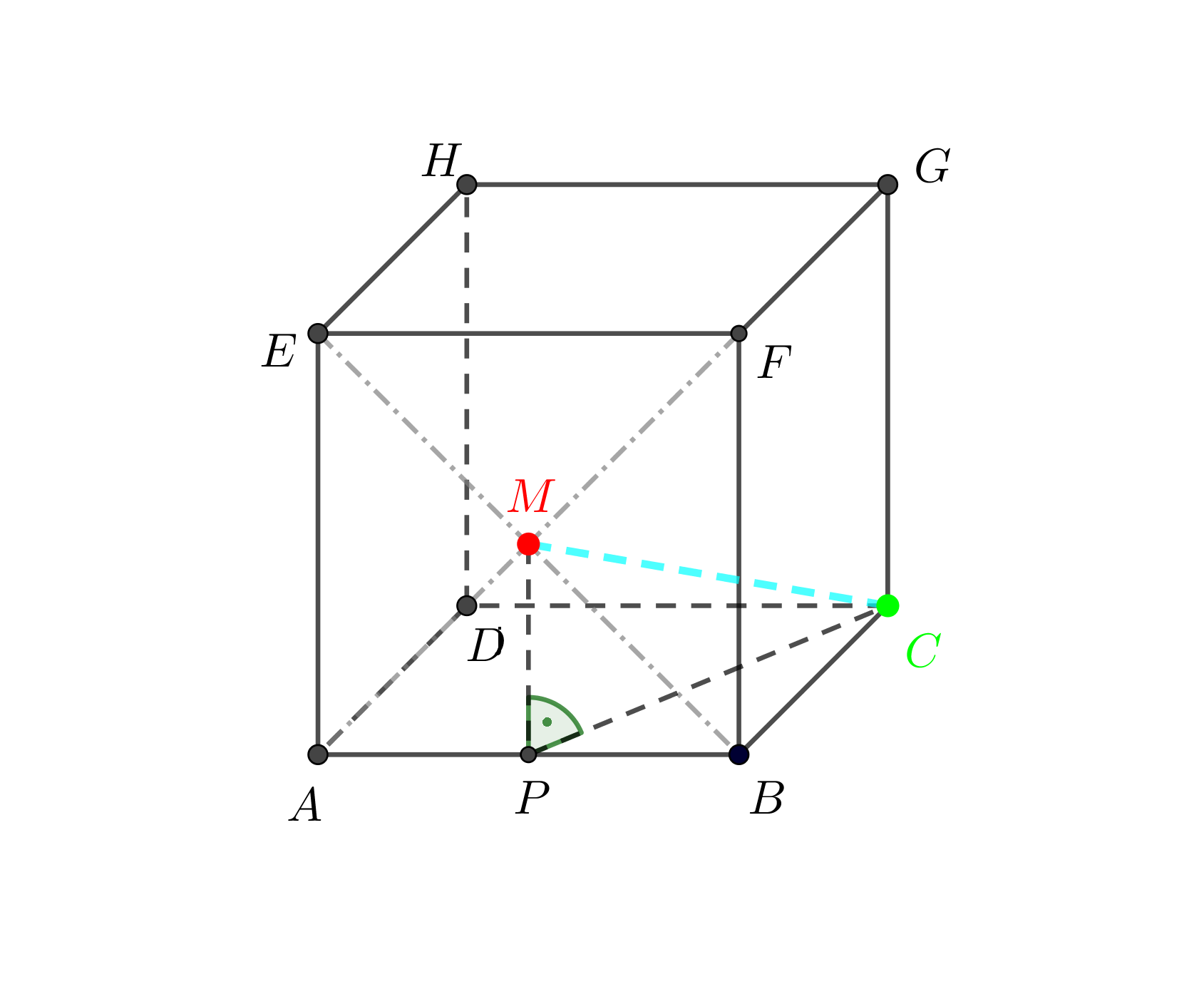
Je dána krychle \(ABCDEFGH\), kde \(|AB|=4 \mbox{ cm}\), a bod \(M\), který je průsečíkem úhlopříček stěny \(ABF\). Určete vzdálenost bodů \(C\), \(M\).
Znázornění situace
Analytické řešení
Zadanou krychli jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
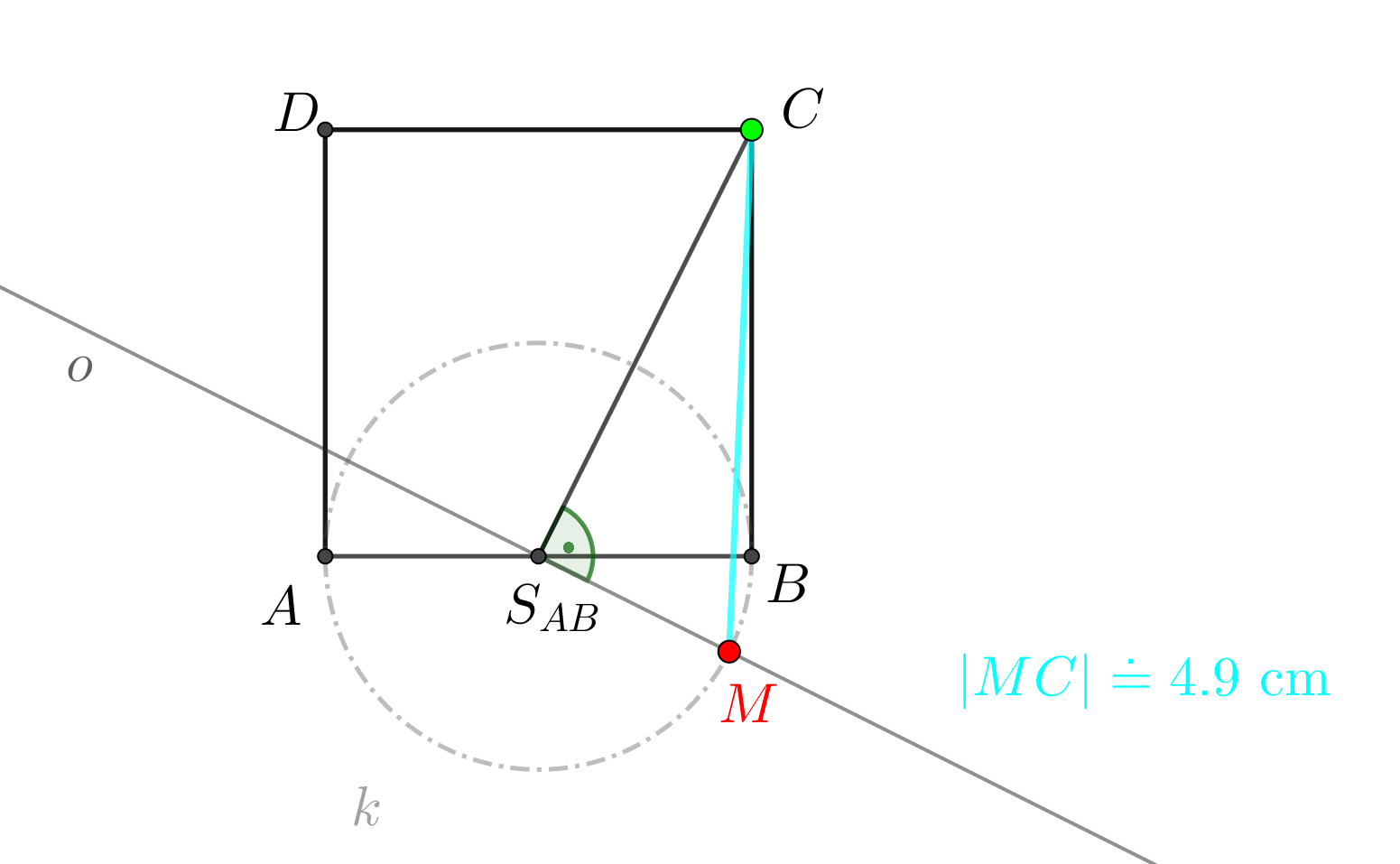
Syntetické konstrukční řešení
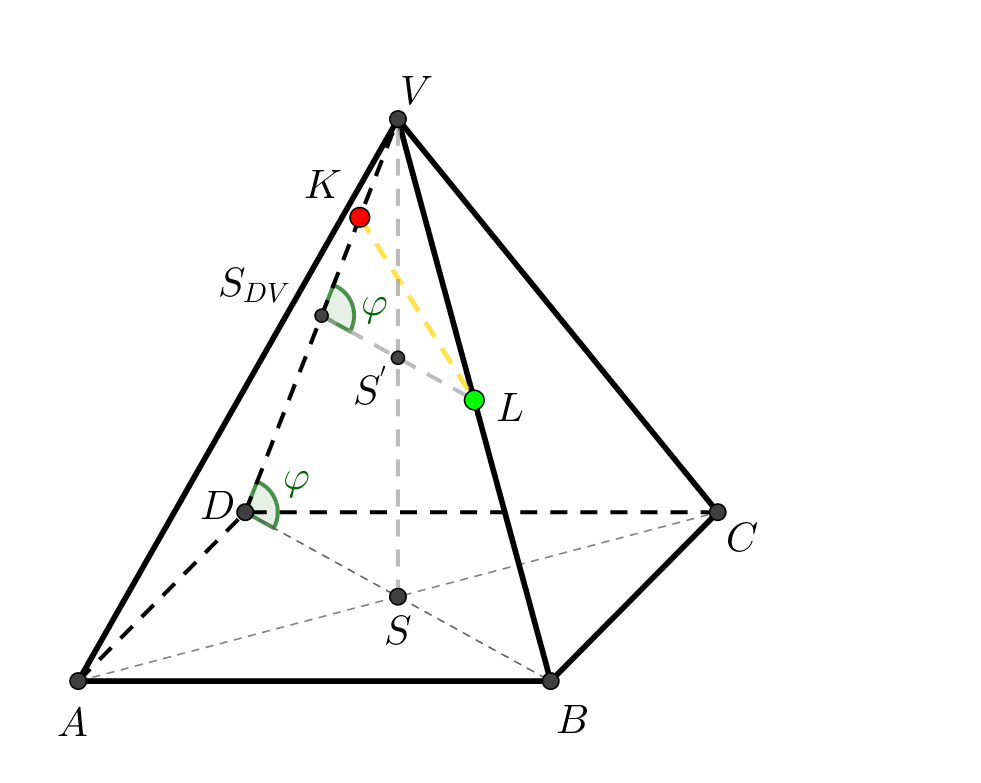
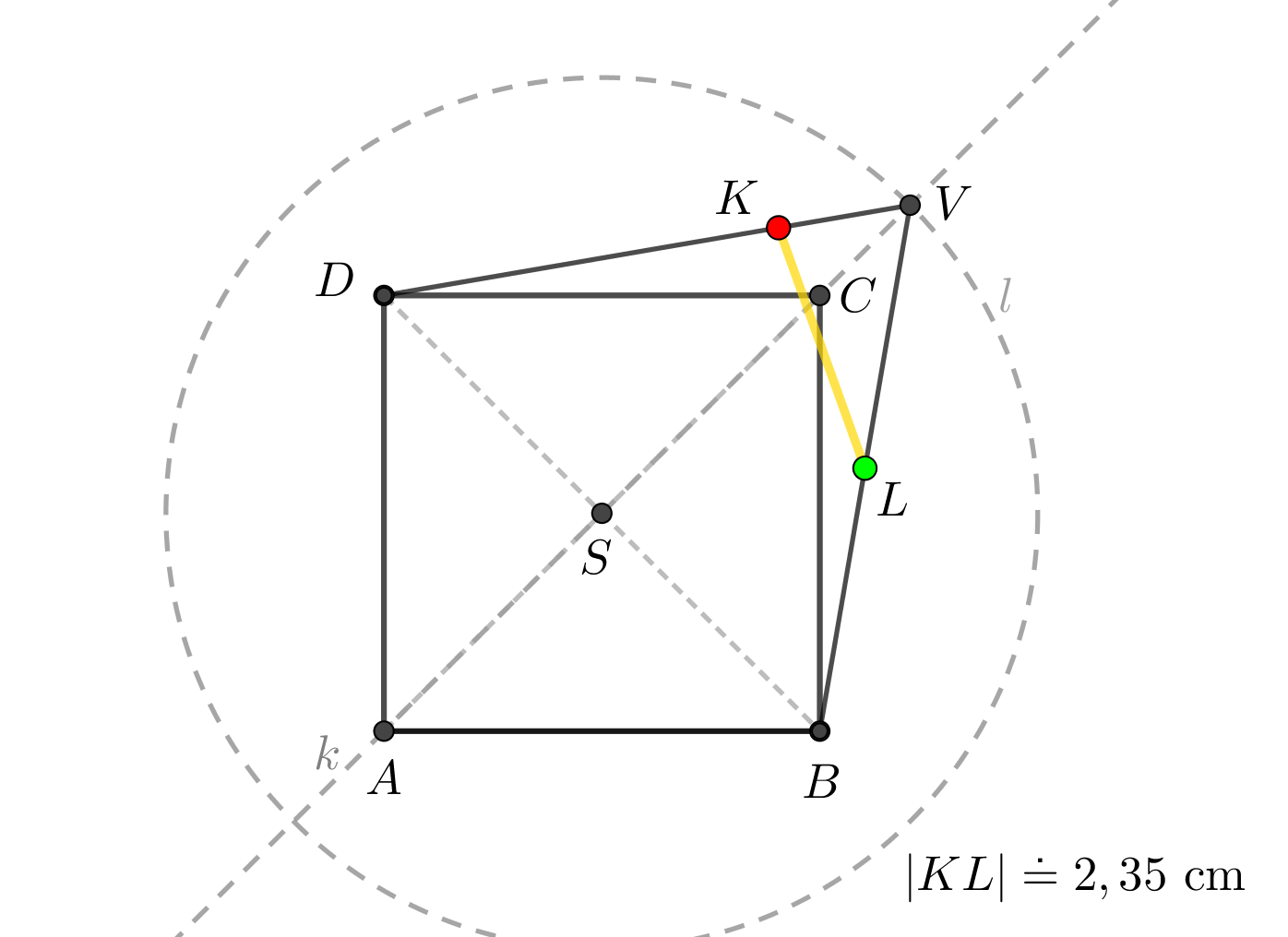
Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 4 \mbox{ cm}\). Dále jsou dány body \(K\), \(L\). Bod \(K\) náleží hraně \(DV\) a platí \(|KV|=\frac{1}{4}|DV|.\) Bod \(L\) je středem hrany \(BV\). Určete vzdálenost bodů \(K\), \(L\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Syntetické početní řešení
Ze zadání víme, že: \(|S_{DV}K|=|KV|=\frac{1}{4}|DV|\) K určení délky \(|S_{DV}K|\) tedy využijeme trojúhelník \(DSV\): \[|S_{DV}K|=\frac{1}{4}\sqrt{\Bigl(2\sqrt{2}\Bigr)^2+4^2}=\frac{1}{4}\sqrt{24} = \frac{\sqrt{6}}{2}\] Abychom mohli určit délku úsečky \(KL\) pomocí kosinové věty, potřebujeme zjistit velikost úhlu \(\varphi=|\angle SDV|=|\angle S'S_{DV}V|\) v trojúhelníku \(DSV\): \[\tan\varphi=\frac{|VS|}{|DS|}=\frac{4}{2\sqrt{2}}=\sqrt{2}\Rightarrow\varphi\doteq 54^\circ 44'\] Nyní již pomocí kosinové věty v \(\triangle S_{DV}LK\) určíme délku \(KL\): \[|KL|^2=|S_{DV}K|^2+|S_{DV}L|^2-2|S_{DV}K||S_{DV}L|\cos\varphi\] \[|KL|^2=\Bigl(\frac{\sqrt{6}}{2}\Bigr)^2+\Bigl(2\sqrt{2}\Bigr)^2-2\frac{\sqrt{6}}{2}2\sqrt{2}\cos(54^\circ 44')\] \[|KL|\doteq 2,35 \mbox{ cm}\]
Syntetické konstrukční řešení
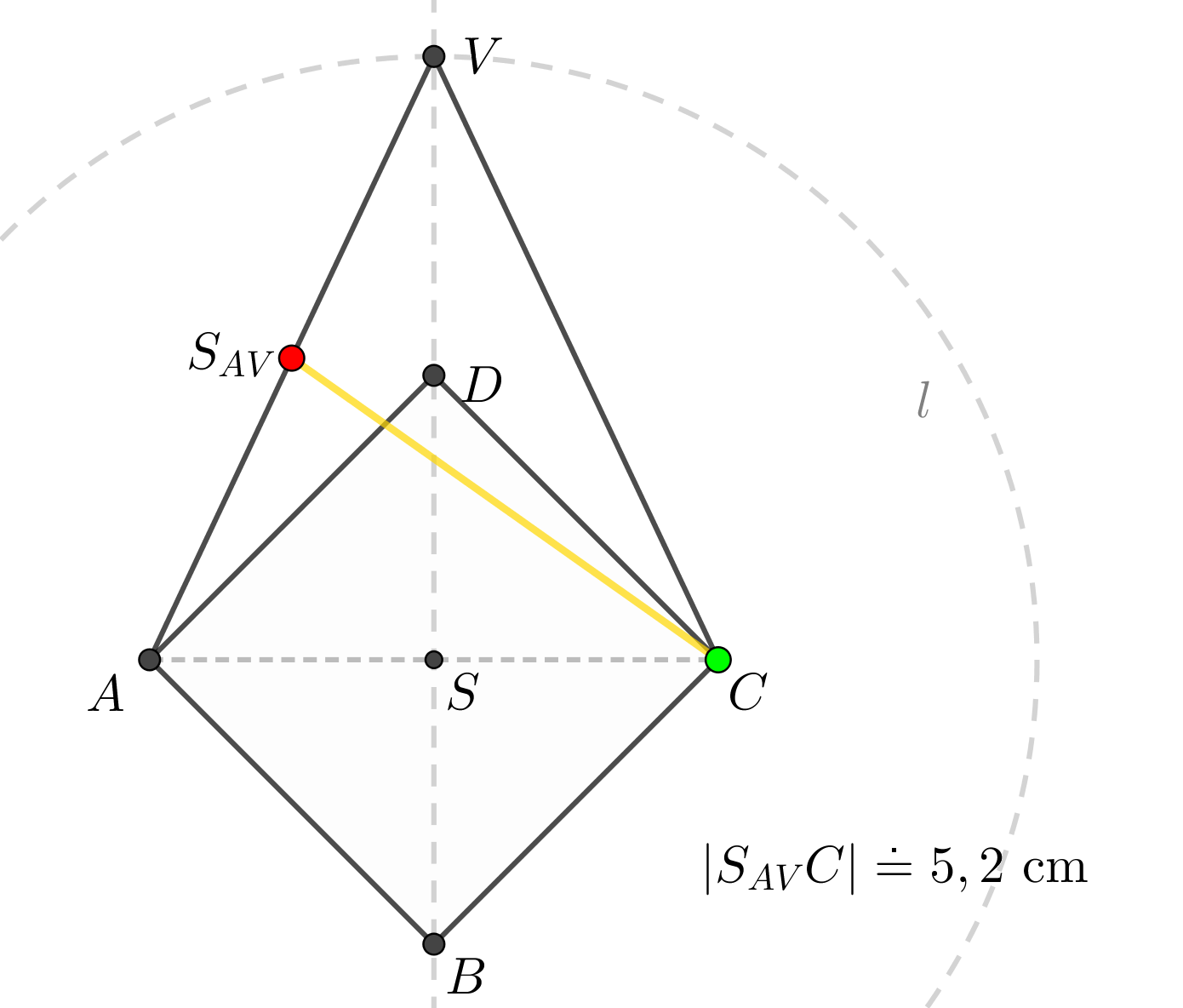
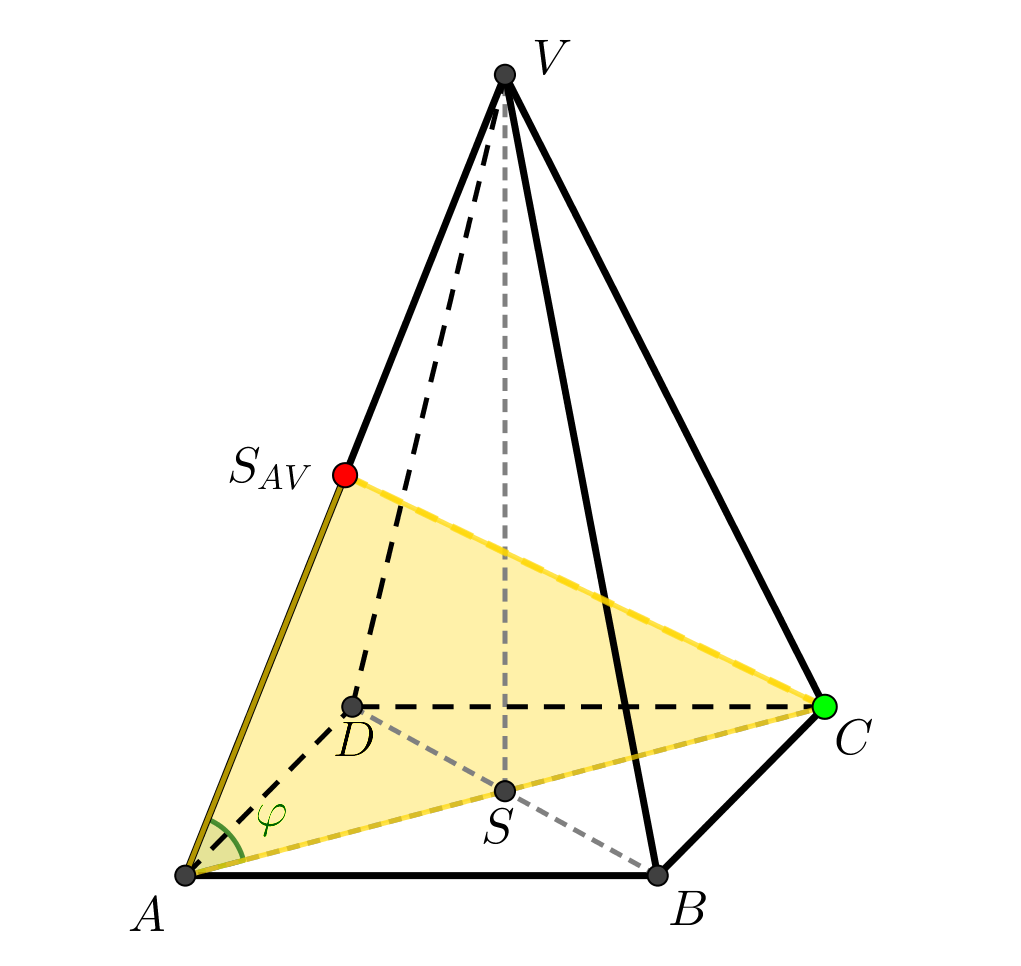
Je dán pravidelný čtyřboký jehlan \(ABCDV\) s podstavou \(ABCD\) o středu \(S\), \(|AB| = 4\mbox{ cm}\), \(|SV| = 6\mbox{ cm}\). Určete vzdálenost bodů \(S_{AV}\), \(C\).
Znázornění situace
Analytické řešení
Zadaný jehlan jsme vhodně umístili do soustavy souřadnic:
Nyní za jednotlivé souřadnice bodů \(S_{AV}\) a \(C\) dosadíme hodnoty dle vhodného umístění do kartézské soustavy souřadnic: \[|S_{AV}C|=\sqrt{(4-1)^2+(4-1)^2+(0-3)^2}=\sqrt{3^2+3^2+(-3)^2}=\sqrt{27}=3\sqrt{3}\doteq 5,2\mbox{ cm}\]
Syntetické početní řešení
Syntetické konstrukční řešení