Řešení metrických úloh v prostoru

Příklady k procvičení:

Je dána krychle ABCDEFGH, |AB| = 6\mbox{ cm}. Určete vzdálenost bodu A od přímky BH.

Znázornění situace | Analytické řešení | Syntetické početní řešení | Syntetické konstrukční řešení

Znázornění situace

Analytické řešení

Zadanou krychli jsme vhodně umístili do soustavy souřadnic:

Směrovým vektorem přímky BH (označme ji p) je vektor \overrightarrow{BH}=(-6;6;6)\sim (-1;1;1).
Parametrické vyjádření přímky p je:

p:\quad x=6-t;\quad y=t;\quad z=t;\quad t\in\mathbb{R}

Najděme obecnou rovnici roviny \varrho, která je kolmá na přímku p a prochází bodem A. Normálový vektor roviny \varrho odpovídá směrovému vektoru přímky p, tj. \overrightarrow{n_\varrho}=(-1;1;1)\sim (1;-1;-1).
Pro obecnou rovnici roviny \varrho platí:

\varrho:\quad x-y-z=0

Nyní určeme průnik P přímky p a roviny \varrho:

p\cap\varrho:6-t-t-t=0

p\cap\varrho:3t=6\quad \Rightarrow\quad t=2

Bod P náleží přímce p, proto platí:

P=[6-t;t;t]

Dosaďme parametr t=2 do souřadnic bodu P:

P=[6-t;t;t]=[4;2;2]

Zbývá nám zjistit vzdálenost bodů A=[0;0;0] a P=[4;2;2]:

|AP|=\sqrt{(4-0)^2+(2-0)^2+(2-0)^2}=\sqrt{16+4+4}=\sqrt{24}\doteq 4,9 \mbox{ cm}

Syntetické početní řešení

Pro výpočet vzdálenosti |AP|, kde bod P je patou kolmice vedené z bodu A k přímce BH, využijeme \triangle ABP. Úhel ABH označíme \beta. Nejlepším nástrojem pro získání délky úsečky AP je goniometrická funkce sinus:

\sin\beta=\frac{|AP|}{|AB|}\Rightarrow |AP|=|AB|\cdot\sin\beta

Abychom tuto funkci mohli použít, musíme vypočítat velikost úhlu \beta. Tu zjistíme pomocí goniometrické funkce tangens v pravoúhlém trojúhelníku ABH. Úhel ABH označíme \beta.
Pro úhel \beta tedy platí:

\tan\beta=\frac{|AH|}{|AB|}=\frac{6\sqrt{2}}{6}=\sqrt{2}\Rightarrow\beta\doteq 54^\circ 44^{'}

Dosaďme velikost úhlu \beta do vztahu pro výpočet |AP|:

|A,BH|=|AP|=|AB|\cdot\sin\beta=6\sin(54^\circ 44^{'})\doteq 4,9 \mbox{ cm}

Syntetické konstrukční řešení

Zápis konstrukce:

\mbox{1) čtverec }ABCD; |AB|=6 \mbox{ cm}
\mbox{2) } k; k\perp AB\wedge D\in k
\mbox{3) } l; l(A,|AC|)
\mbox{4) } H; H\in l\cap k
\mbox{5) } m; m\perp BH \wedge A\in m
\mbox{6) } P;P\in m\cap BH

Provedením konstrukce jsme získali |AP|=|A,BH|.

Je dána krychle ABCDEFGH, |AB| = 6\mbox{ cm}. Určete vzdálenost bodu E od přímky AS_{FH}.

Znázornění situace | Analytické řešení | Syntetické početní řešení | Syntetické konstrukční řešení

Znázornění situace

Analytické řešení

Zadanou krychli jsem vhodně umístili do soustavy souřadnic:

K řešení využijeme doplnění na rovnoběžník ES_{FH}AN (viz obrázek), jehož výška je rovna hledané vzdálenosti bodu E od přímky AS_{FH}.
Výšku rovnoběžníku ES_{FH}AN odvodíme z jeho obsahu. Obsah rovnoběžníku získáme vektorovým součinem vektorů \overrightarrow{ES_{FH}}=(3;3;0), \overrightarrow{AS_{FH}}=(3;3;6).

\begin{eqnarray*}S&=&|\overrightarrow{ES_{FH}}\times\overrightarrow{AS_{FH}}|\\ &=&\bigl|(3\cdot 6-0\cdot 3;0\cdot 3-3\cdot 6;3\cdot 3-3\cdot 3)\bigr|\\ &=&|(18;-18;0)|\\ &=&18\sqrt{2}\end{eqnarray*}

Nyní již můžeme vypočítat hledanou výšku rovnoběžníku ES_{EG}AN:

|EP|=\frac{S}{|AS_{FH}|}=\frac{18\sqrt{2}}{\sqrt{3^2+3^2+6^2}}=\frac{18\sqrt{2}}{\sqrt{54}}=\frac{18\sqrt{2}}{3\sqrt{6}}=\frac{6}{\sqrt{3}}=2\sqrt{3}\doteq 3,46\mbox{ cm}

Syntetické početní řešení

Během řešení se budeme pohybovat v trojúheníku AS_{FH}E. Abychom mohli vypočítat vzdálenost |EP| (vzdálenost bodu E od přímky AS_{FH}, bod P je patou výšky vedené z bodu E v trojúhelníku AS_{FH}E) musíme určit velikost úhu EAS_{FH}.
Velikost úhlu EAS_{FH} zjistíme pomocí goniometrické funkce tangens:

\tan(\angle EAS_{FH})=\frac{|ES_{FH}|}{|AE|}=\frac{3\sqrt{2}}{6}=\frac{\sqrt{2}}{2}\Rightarrow |\angle EAS_{FH}|\doteq 35^\circ 16^{'}

Nyní využijeme goniometrickou funkci sinus, abychom získali velikost úsečky EP:

\sin(\angle EAS_{FH}) = \frac{|EP|}{|AE|}\Rightarrow |EP|=|AE|\cdot\sin(\angle EAS_{FH})=6\sin(35^\circ 16^{'})\doteq 3,46\mbox{ cm}

Syntetické konstrukční řešení

Zápis konstrukce:

\mbox{1) čtverec } ABCD; |AB|=4 \mbox{ cm}
\mbox{2) } \leftrightarrow o; o\perp \overline{AC} \wedge C\in o
\mbox{3) } \leftrightarrow p; p\perp \overline{AC} \wedge A\in p
\mbox{4) } k; k(C,|AB|)
\mbox{5) } l; l(A,|AB|)
\mbox{6) } E; E\in p\cap l
\mbox{7) } G; G\in k\cap o \wedge G\in\longmapsto ACE
\mbox{8) } S_{FH};S_{FH}\in EG\wedge |ES_{FH}|=|S_{FH}G|
\mbox{9) } \leftrightarrow m; m\perp \overline{AS_{FH}} \wedge E\in m
\mbox{10) } P; m\cap \overline{AS_{FH}} = \{P\}

Provedením konstrukce jsme získali vzdálenost bodů E a P, čímž jsme sestrojili vzdálenost bodu E od přímky AS_{FH}

Je dán pravidelný pětiboký jehlan ABCDEV s podstavou ABCDE o středu S, |AB| = 4\mbox{ cm}, |SV| = 4\mbox{ cm}. Určete vzdálenost bodu A od přímky DV.

Znázornění situace | Analytické řešení | Syntetické početní řešení | Syntetické konstrukční řešení

Znázornění situace

Analytické řešení

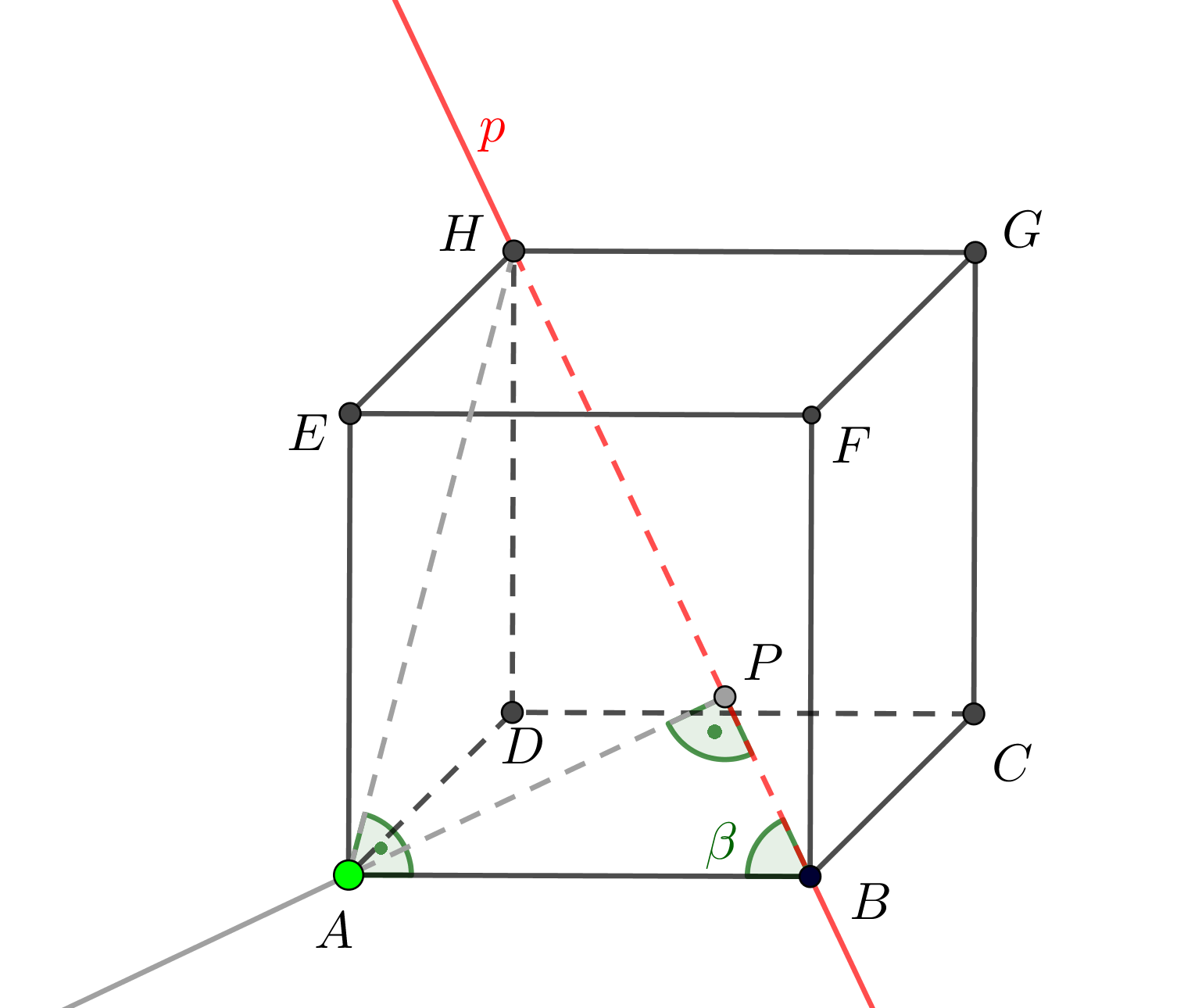
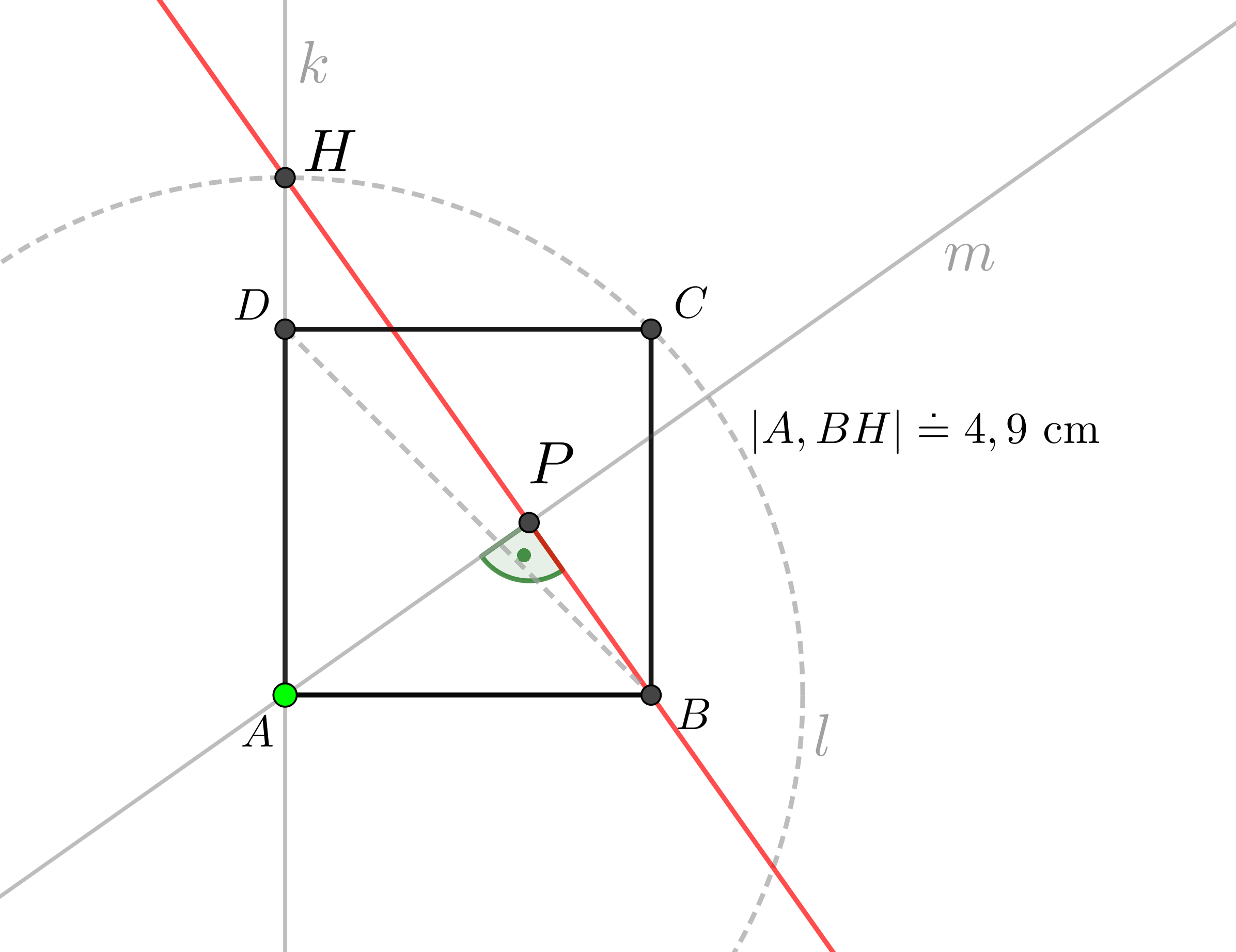
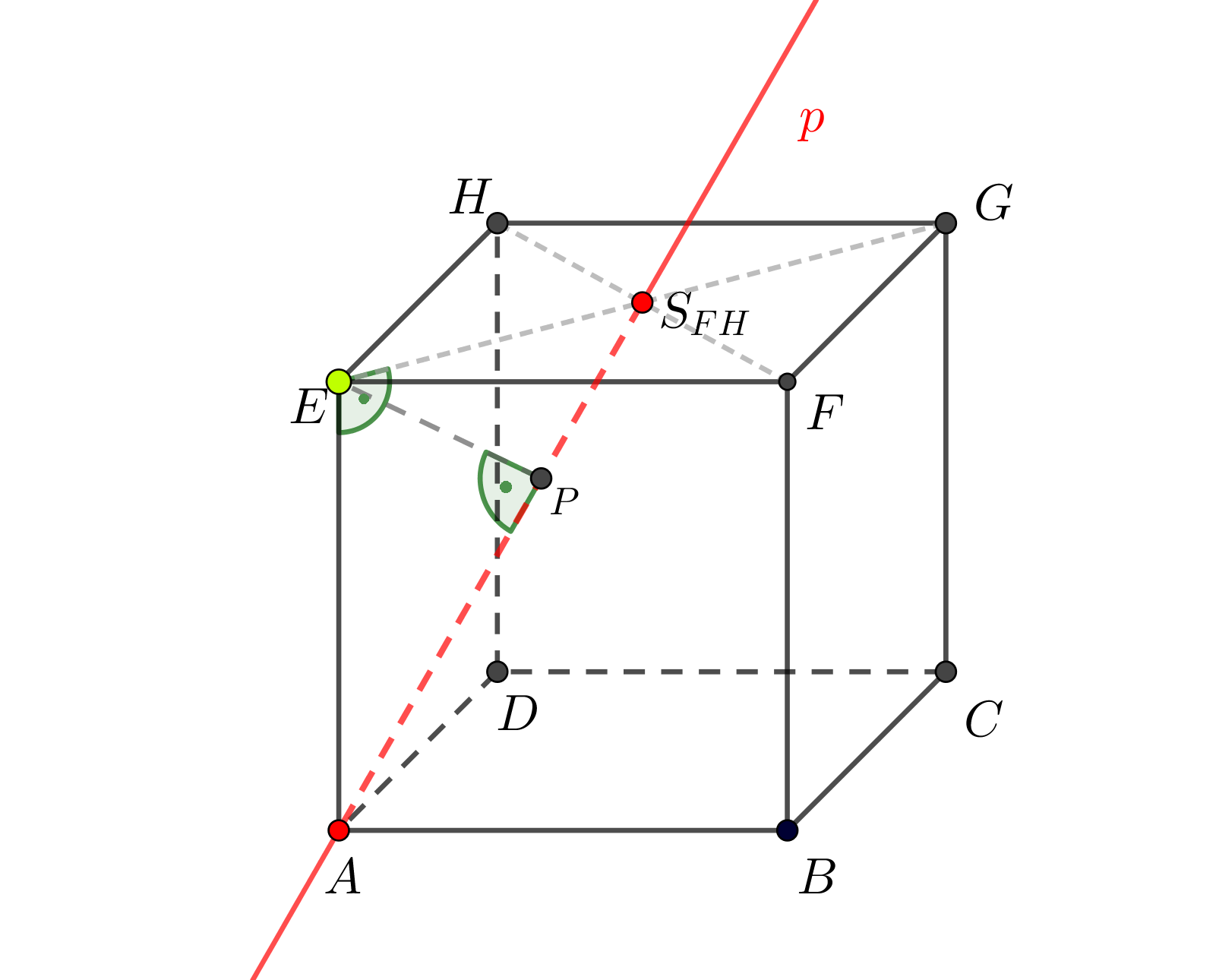
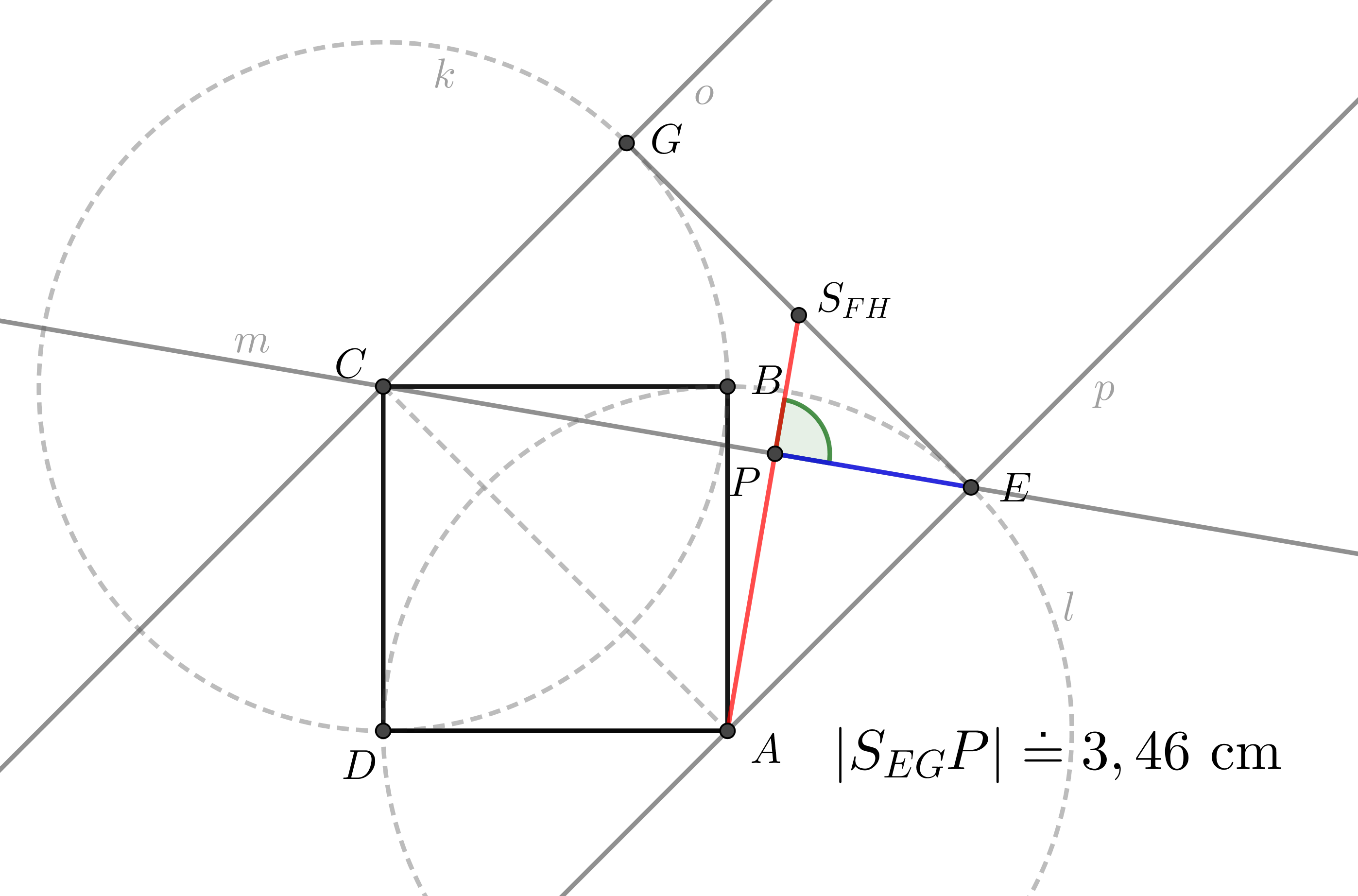
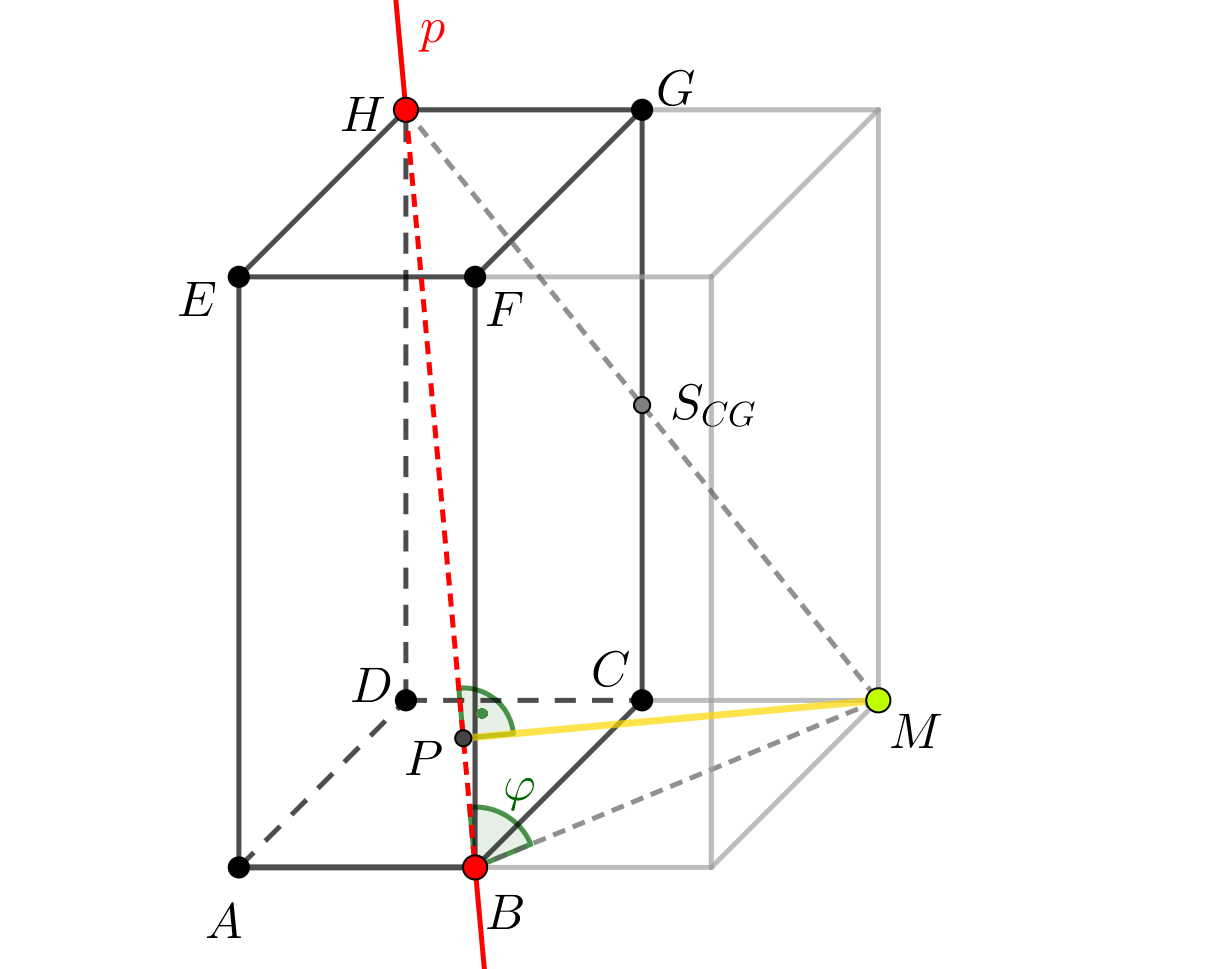
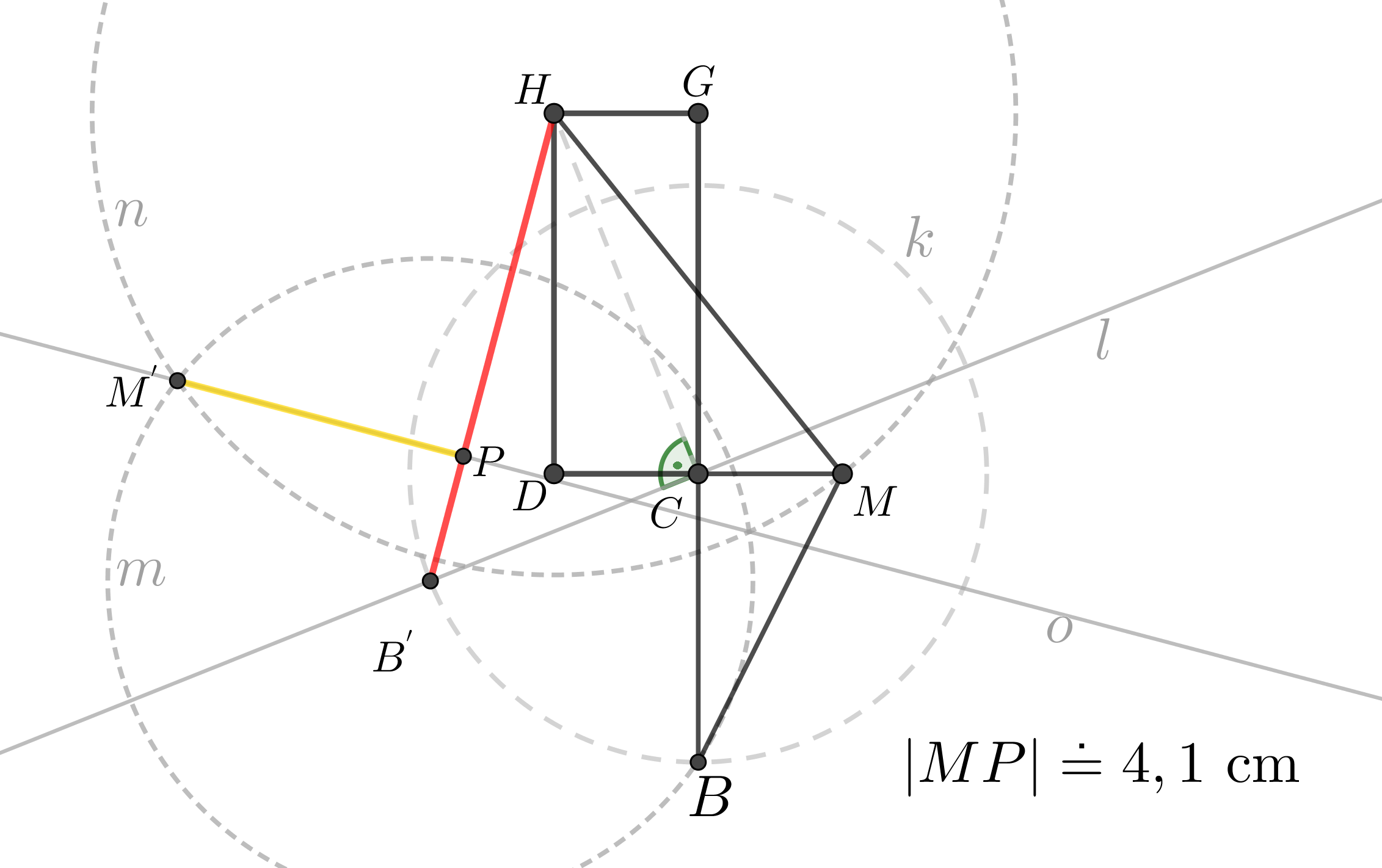
Zadaný pětiboký jehlan jsme vhodně umístili do soustavy souřadnic:

Souřadnice bodů A, B jsme odvodili z trojúhelníku ABS, jehož strana AB má délku 4 \mbox{ cm} a úhel při vrcholu S má velikost 72^\circ. Obdobným způsobem jsme získali i souřadnice bodu D. Zde jsme vycházeli z trojúhelníku DCS. Souřadnice jsou zaokrouhleny na dvě desetinná místa.

Směrovým vektorem přímky DV je vektor \overrightarrow{DV}=(3,4;0;4).
Parametrické vyjádření přímky DV je:

p:\quad x=-3,4+3,4t;\quad y=0;\quad z=4t;\quad t\in\mathbb{R}

Najděme obecnou rovnici roviny \varrho, která je kolmá na přímku DV a prochází bodem A. Normálový vektor roviny \varrho odpovídá směrovému vektoru přímky DV, tj. \overrightarrow{DV}=\overrightarrow{n_\varrho}=(3,4;0;4).
Do obecné rovnice 3,4x+4z+d=0 dosadíme souřadnice bodu A a získáme d=-9,35.
Pro obecnou rovnici roviny platí:

\varrho:\quad 3,4x+4z-9,35=0

Nyní určeme průnik P přímky DV a roviny \varrho:

\leftrightarrow DV\cap\varrho:3,4.(-3,4)+3,4^2t+16t -9,35=0

\leftrightarrow DV\cap\varrho:27,56t=20,91\quad \Rightarrow\quad t\doteq 0,76

Bod P náleží přímce DV, proto platí:

P=[-3,4+3,4t;0;4t]

Dosaďme parametr t=0,76 do souřadnic bodu P:

P=[-3,4+3,4t;0;4t]\doteq [-0,82;0;3,04]

Zbývá nám zjistit vzdálenost bodů A=[2,75;-2;0] a P=[-0,82;0;3,04]:

|AP|=\sqrt{(-0,82-2,75)^2+(-2)^2+(3,04)^2}=\sqrt{(-3,57)^2+4+(3,04)^2}\doteq 5,1 \mbox{ cm}

Syntetické početní řešení

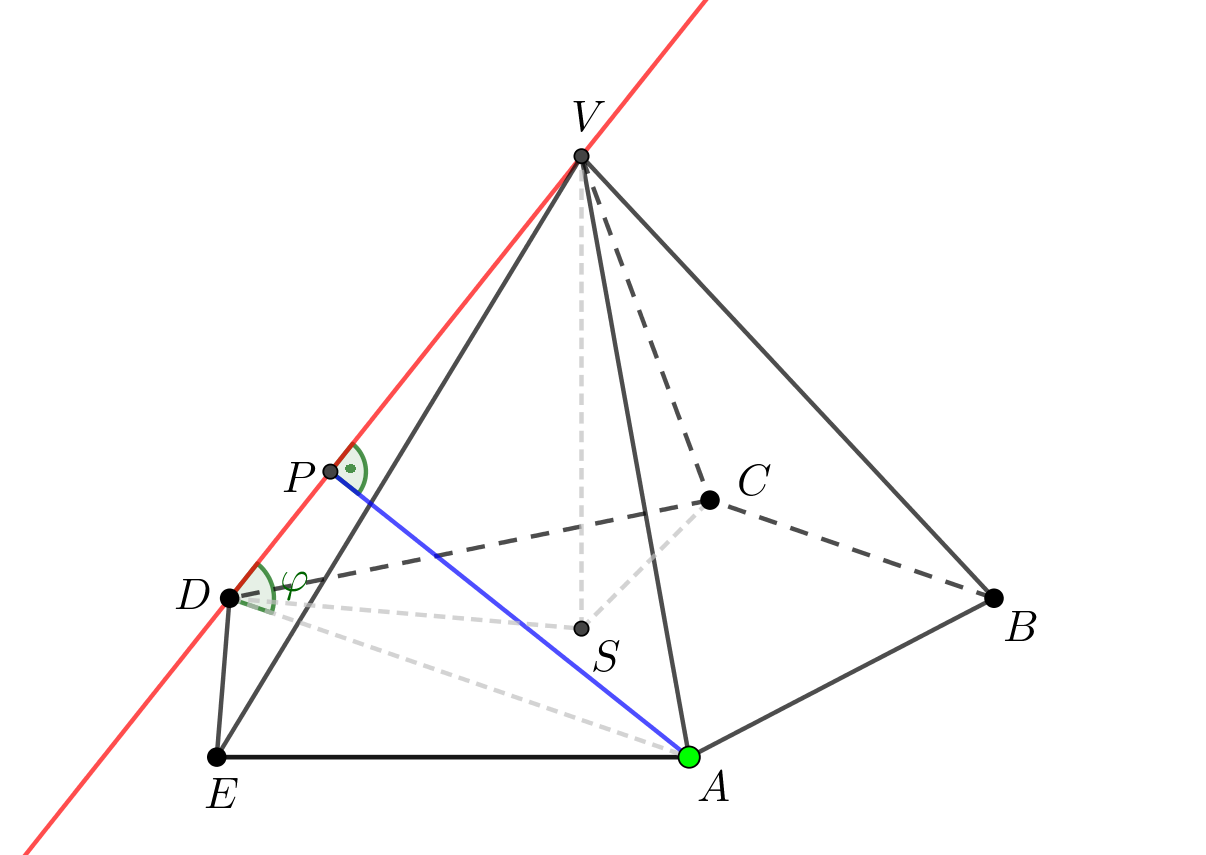
Vzdálenost bodu A od přímky DV odpovídá výšce AP v trojúhelníku DAV. Abychom požadovanou délku úsečky získali, musíme zjistit velikost úhlu VDA a velikosti stran daného trojúhelníku.
Velikost úhlu můžeme získat například z trojúhelníku VDA pomocí kosinové věty. Pojďme tedy vypočítat velikost úsečky DS, která je prvním krokem k získání potřebného úhlu.
Velikost úsečky DS dostaneme užitím goniometrické funkce sinus v trojúhelníku DSS_{CD}:

|DS|=\frac{|DS_{CD}|}{\sin 36^\circ}=\frac{2}{\sin 36^\circ}\doteq 3,4\mbox{ cm}

Pro délky hran AV, DV, jež jsou rameny v trohúhelníku VDA, platí:

|AV|=|DV|=\sqrt{|SV|^2+|DS|^2}=\sqrt{4^2+3,4^2}\doteq 5,25\mbox{ cm}

Dalším chybějícím údajem z trojúhelníku VDA je délka strany DA. Získejme ji kosinovou větou v trojúhelníku DEA:
Předpokládáme znalost velikosti úhlu DEA, tj. |\angle DEA|=108^\circ.

\begin{eqnarray*}|DA|^2&=&|DE|^2+|EA|^2-2|DE||EA|\cos(\angle DEA)\\ &=&4^2+4^2-2\cdot 4\cdot 4\cdot \cos 108^\circ\\ &=&32-32\cos 108^\circ \end{eqnarray*}

|DA|\doteq 6,47\mbox{ cm}

Pro velikost úhlu VDA tedy platí:

\cos(\angle VDA)=\frac{|AV|^2-|DV|^2-|DA|^2}{-2|DV||DA|}=\frac{|DA|}{2|DV|}=\frac{6,47}{2\cdot 5,25}\doteq 0,62\Rightarrow |\angle VDA|\doteq 51^\circ 41^{'}

Nyní jen použijeme goniometrickou funkci sinus na trojúhelník PDA a získáme |AP|:

|AP|=|DA|\cdot\sin(\angle VDA)=6,47\cdot\sin(51^\circ 41^{'})\doteq 5,1\mbox{ cm}

Syntetické konstrukční řešení

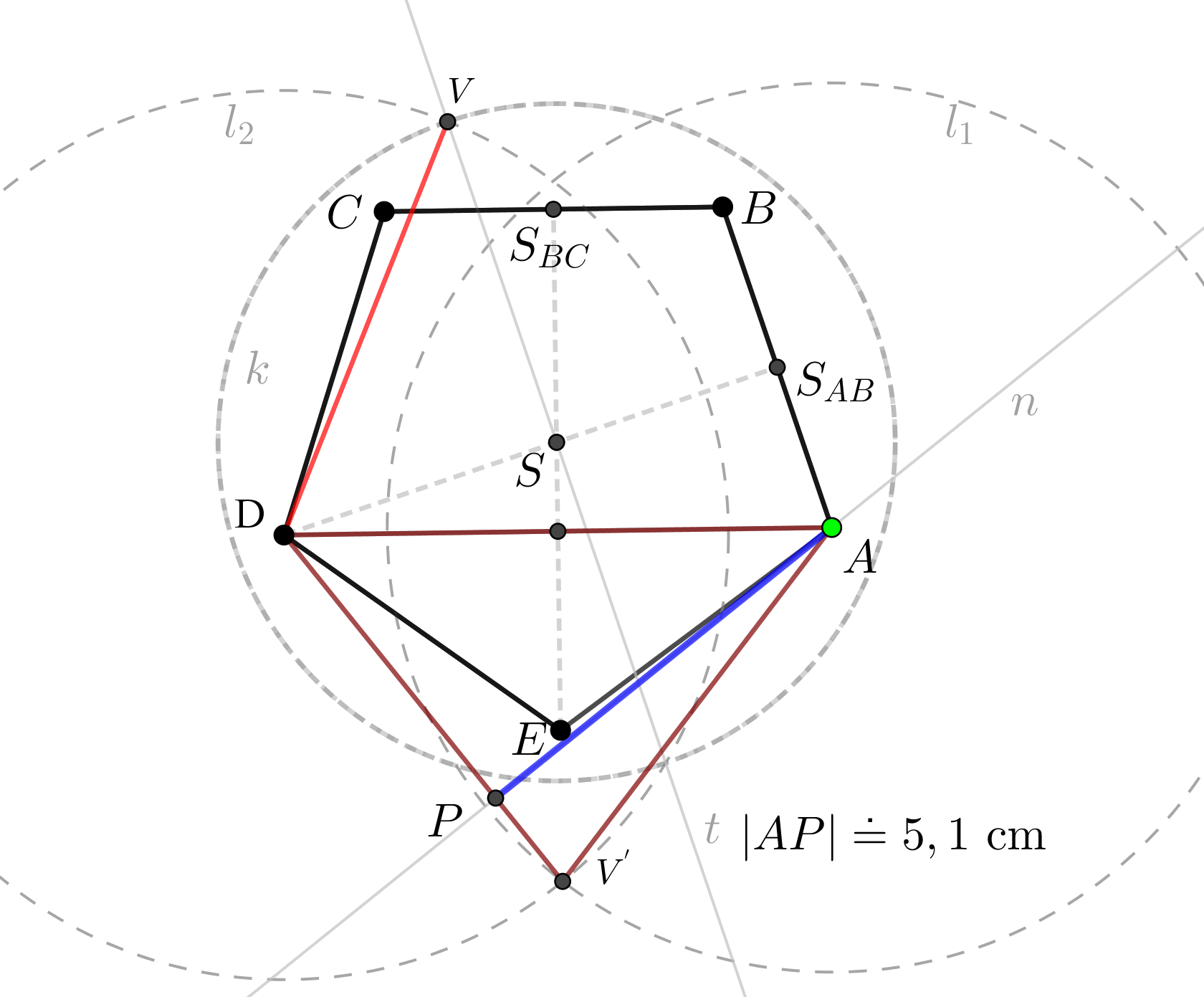
Zápis konstrukce:

\mbox{1) pravidelný pětiúhelník } ABCDE; |AB|=4 \mbox{ cm}
\mbox{2) } S_{AB}; S_{AB}\mbox{ je střed strany }AB
\mbox{3) } S_{BC}; S_{BC}\mbox{ je střed strany }BC
\mbox{4) } S; \overline{DS_{AB}}\cap \overline{ES_{BC}} = \{S\}
\mbox{5) } t; t\perp \overline{DS_{AB}}\wedge S\in t
\mbox{6) } k; k(S,4\mbox{ cm})
\mbox{7) } V; V\in t\cap k
\mbox{8) } l_1; l_1(A,|DV|)
\mbox{9) } l_2; l_2(D,|DV|)
\mbox{10) } V^{'}; V^{'}\in l_1\cap l_2
\mbox{11) } n; n\perp\overline{DV^{'}}\wedge A\in n
\mbox{12) } P; n\cap \overline{DV^{'}} = \{P\}

Provedením konstrukce jsme získali vzdálenost bodů A, P, čímž jsme sestrojili vzdálenost bodu A od přímky DV.

Je dán kvádr ABCDEFGH, |AB| = 2\mbox{ cm}, |BC| = 4\mbox{ cm}, |BF| = 5\mbox{ cm}. Dále je dán bod M takový, že bod C je středem úsečky DM. Určete vzdálenost bodu M od přímky BH.

Znázornění situace | Analytické řešení | Syntetické početní řešení | Syntetické konstrukční řešení

Znázornění situace

Analytické řešení

Zadanou krychli jsem vhodně umístili do soustavy souřadnic:

Směrovým vektorem přímky BH je vektor \overrightarrow{BH}=(-2;4;5).
Parametrické vyjádření přímky BH je:

\leftrightarrow BH:\quad x=-2t,\quad y=-4+4t,\quad z=5t,\quad t\in\mathbb{R}

Normálový vektor roviny \varrho odpovídá vektoru \overrightarrow{BH}=(-2;4;5).
Obecná rovnice roviny \varrho kolmé na přímku BH a procházející bodem M je:

\varrho:\quad 2x-4y-5z-4=0

Nyní dosadíme parametrické vyjádření rovnice přímky BH do obecné rovnice roviny \varrho:

2\cdot (-2t)-4\cdot (-4+4t)-5\cdot (5t)-4=0

-4t+16-16t-25t-4=0

45t=12\Rightarrow t=\frac{4}{15}

Pro průsečík přímky BH s rovinou \varrho platí:

P=[-2t;-4+4t;5t]=\Biggl[-\frac{8}{15};-\frac{44}{15};\frac{4}{3}\Biggr]

Velikost úsečky MP je rovna:

|MP|=\sqrt{\Biggl(-\frac{8}{15}-2\Biggr)^2+\Biggl(-\frac{44}{15}-0\Biggr)^2+\Biggl(\frac{4}{3}-0\Biggr)^2}\doteq 4,1\mbox{ cm}

Syntetické početní řešení

Pro snažší počítání doplníme shodný kvádr s kvádrem ABCDEFGH vedle již stávajícího kvádru tak, že bod M je součástí podstavy nového kvádru (viz obrázek).
K výpočtu využijeme trojúhelník HBM, pro jehož délky stran platí:

|BH|=\sqrt{|CB|^2+|CH|^2}=\sqrt{4^2+(\sqrt{5^2+2^2})^2}=3\sqrt{5}

|HM|=\sqrt{(2|HG|)^2+|CG|^2}=\sqrt{\bigl(2\cdot 2\bigr)^2+5^2}=\sqrt{41}

|BM|=\sqrt{|AB|^2+|BC|^2}=\sqrt{2^2+4^2}=2\sqrt{5}

Patu kolmice z bodu M k přímce BH označíme P.
Abychom mohli určit délku úsečky MP musíme vypočítat velikost úhlu HBM (označme jej dále \varphi). Velikost úhlu \varphi získame pomocí kosinové věty:

\cos\varphi=\frac{|HM|^2-|BH|^2-|BM|^2}{-2|BH||BM|}=\frac{\bigl(\sqrt{41}\bigr)^2-\bigl(3\sqrt{5}\bigr)^2-\bigl(2\sqrt{5}\bigr)^2}{-2\cdot 3\sqrt{5}\cdot 2\sqrt{5}}=\frac{41-9\cdot 5-4\cdot 5}{-2\cdot 3\cdot 2\cdot 5}=\frac{2}{5}\Rightarrow\varphi\doteq 66^\circ 25^{'}

Již známe velikost úhlu \varphi, tak můžeme pomocí goniometrické funkce sinus v trojúhelníku PBM určit délku úsečky MP:

\sin\varphi=\frac{|MP|}{|BM|}\Rightarrow|MP|=|BM|\cdot\sin\varphi=2\sqrt{5}\cdot\sin(66^\circ 25^{'})\doteq 4,1\mbox{ cm}

Syntetické konstrukční řešení

Zápis konstrukce:

Nejdříve sestrojíme strany trojúhelníku HBM, abychom jej mohli následně sestrojit podle věty sss. Výška sestrojeného trojúhelníku bude odpovídat hledané vzdálenosti.
Při konstrukci trojúhelníku HBM budeme již existující vrcholy označovat apostrofem.

\mbox{1) obdélník } DCGB; |DC|=2 \mbox{ cm a } |CG|=5\mbox{ cm}
\mbox{2) } M; C\mbox{ je středem } \overline{DM}
\mbox{3) } k; k(C,4\mbox{ cm})
\mbox{4) } B; \leftrightarrow{GC}\cap k = \{B\}
\mbox{5) } \overline{BM}
\mbox{6) } \leftrightarrow l; l\perp \overline{CH} \wedge C\in l
\mbox{7) } B^{'}; B^{'}\in l\cap k
\mbox{8) } \overline{B^{'}H}
\mbox{9) } n; n(H,|HM|)
\mbox{10) } m; m(B^{'},|BM|)
\mbox{11) } M^{'}; M^{'}\in n\cap m
\mbox{12) } \triangle HM^{'}B^{'}
\mbox{13) } \leftrightarrow o; o\perp \overline{B^{'}H} \wedge M^{'}\in o
\mbox{14) } P;\{P\}=o\cap\overline{B'H}

Provedením konstrukce jsme získali vzdálenost bodů M, P, čímž jsme sestrojili vzdálenost bodu M od přímky BH.

Řešení metrických úloh v prostoru

Úvod

Odchylky

Vzdálenosti