Učební texty ke cvičením

Soubor A:

34stránkový učební text v PDF, zachycující průběh všech cvičení v ZS 2010/11.
Text, rozdělený do jednotlivých cvičení, naleznete v dalším paragrafu.
Odhalení jakýchkoli překlepů, nepřesností nebo chyb velmi uvítám.

 Soubor B:

Soubor obsahuje (m.j.) naskenované následující strany ze skript
"Doktor, John, Kopáček: Příklady z MA VI - PDR":

str. 60- 69: příklady na kanonický tvar a klasifikaci rovnic 2. řádu
str. 127-143: příklady na Fourierovu metodu separace, pro hyperb. rovnice
str. 179-196: příklady na Fourierovu metodu separace, pro elipt. rovnice
str. 215-233: příklady na Fourierovu metodu separace, pro parab. rovnice

Soubor C: ještě nějaké příklady:     

Průběh jednotlivých cvičení, separátní materiály k jednotlivým cvičením


No. Datum Popis cvičení Text
ke cvičení
1.  29.09.2010 Elementy plošné integrace, parametrizace plochy, integrál prvního a druhého druhu a vztah mezi nimi. Plošný element, vektorový součin (d-1) vektorů v Rd, Grammův determinant. Gauss-Greenovy-Ostrogradského formule
2.  06.10.2010 Odvození některých PDR z fyzikálních principů: rovnice vedení tepla, rovnice minimální plochy.
3.  13.10.2010 Multinomická věta, Gaussův integrál, gamma funkce, sférické souřadnice v m dimenzích, plocha sféry a objem koule v m dimenzích.
4.+5.  20.+27.10.2010 Řešení kvazilineárních rovnic 1. řádu metodou charakteristik, implicitní a lokální existence. Řešení systému lineárních rovnic 1. řádu s konstantní diagonalizovatelnou maticí.
5.+6.  27.10+3.11.2010 Různé varianty a možnosti zobecnění Cauchyho-Kowalevské věty. Nestabilita řešení Laplaceovy rovnice při "nevhodně zadaných počátečních podmínkách" - Hadamardův protipříklad. D'Alembertův vzorec pro vlnovou rovnici v jedné dimenzi, jeho komplexní analogie pro Laplaceovu rovnici.
7.  10.11.2010 Kanonický tvar a klasifikace rovnic druhého řádu. Rovnice eliptická, parabolická hyperbolická. Převádění na kanonický tvar v bodě a možnosti dalších úprav prvních a nultých derivací.
8.  17.11.2010 Cvičení odpadlo: státní svátek. -
9.  24.11.2010 Odvození Poissonova integrálu: řešení Dirichletovy úlohy pro Laplaceovu rovnice na kouli, metodou zrcadlení (kulové inverze). Diskuse případu v dimenzích 3 a výše, a v dimenzi 2. Převod Poissonova integrálu v dimenzi 2 do polárních souřadnic.
10.+11.  1.+8.12.2010 Laplaceova-Poissonova rovnice na obdélníku: řešení Fourierovou metodou rozdělení (separace) proměnných. Podrobné, leč formální sestavení řešení pro nulovou pravou stranu a nenulovou okrajovou podmínku. Diskuse formálního výsledku - konvergence řady, spojitost a hladkost výsledné funkce a nabývání O.P. Náznak postupu pro nenulovou pravou stranu.
11.+12.  8.+14.12.2010 Převod Laplaceova operátoru do polárních souřadnic. Dirichletova úloha pro Laplaceovu rovnici na kruhu, řešení ve tvaru řady, srovnání s řešením pomocí Poissonova integrálu. Rovnice vedení tepla na úsečce, její řešení Fourierovou metodou.
13.  22.12.2010 Cvičení odpadlo: vánoce. -
14.  5.1.2011 Zápočtová písemka. -
15.  12.1.2011 Zápočty, dodatky, doplňky, dotazy. -


Zápočtová písemka

  • 5.1.: na cvičení se psala písemka, která obsahovala 3 příklady:
    1. řešení PDR 1. řádu metodou charakteristik
    2. převedení PDR 2. řádu na kanonický tvar a určení typu
    3. řešení PDR Fourierovou metodou rozdělení proměnných
  • Písemka nebyla povinná, viz "pravidla pro udělení zápočtu".
    Přítomnost na písemce se však hodnotila 10 body, jako každá jiná přítomnost na cvičení.

    Při vlastní písemce bylo dovoleno používat jakékoli materiály, tištěné či psané.
    Co však nebylo dovoleno používat: jakékoli elektronické zařízení, jakákoli pomoc či nápověda od druhé osoby.

Zadání písemky:      Řešení písemky (rukopis, snad ho přečtete):     

Prezence, zápočty


Pravidla pro udělení zápočtu pro prezenční studenty

  1. účast alespoň na 3 cvičeních v semestru, a zároveň
  2. zisk 100 bodů, přičemž body je možno získat takto:
    1. 10 bodů za každou účast na cvičení
    2. 0-10 bodů za každý z 3 příkladů písemky (která se konala 5.1. v době cvičení)
    3. 0-5 bodů za každý z příkladů zadaných cvičícím "na doma"
Písemku tedy neebylo nutno psát, pokud jste dali dohromady 100 bodů jinak,
výsledky písemky však mohou drobně pomoci i u zkoušky (viz pravidla zkoušek).

Pravidla pro udělení zápočtu pro kombinované studenty

Udělení zápočtu budeme řešit individuálně, bude vázáno na spočtení určitého počtu příkladů a/nebo zpracování
některého z otevřených témat z materiálů ke cvičením. Prosím kontaktujte mě.


Písemka dopadla vcelku slušně, s průměrným bodovým ziskem 19 bodů. Považoval jsem za pozitivní, že se jí zúčastnili i ti, kteří již měli zápočet zajištěn.

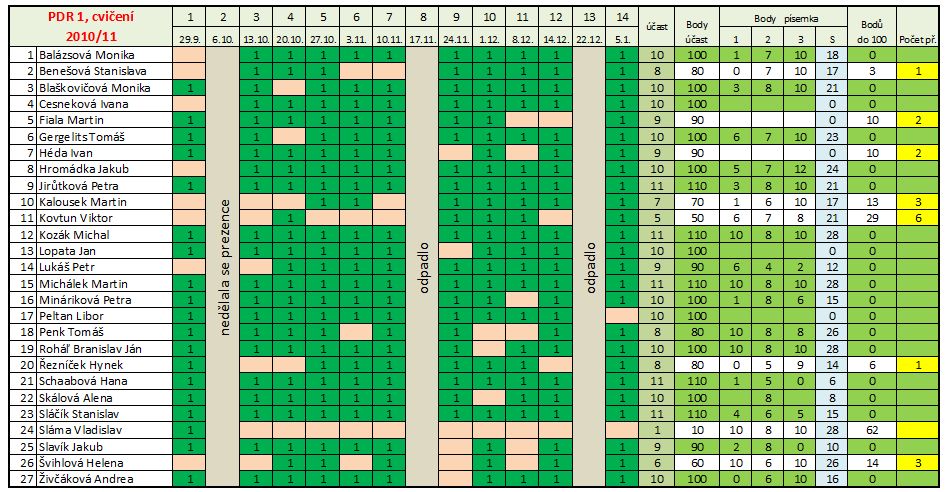
Tabulka účastí s výsledky písemky ukazuje, kolik příkladů "na doma" (čísla na žlutém podkladu) chybí některým účastníkům cvičení k zisku zápočtu. Některé případy je potřeba řešit individuálně.

Ostatním mohu zapsat zápočet, buď na cvičení 12.1., nebo u zkoušky. Příklady na spočtení lze zadat i elektronicky (proto je na této stránce nahoře naskenován kus "příkladových" skript a jsou k dispozici i další příklady - při elektronickém zadání se budu odvolávat právě na tyto soubory A, B, C.)