Objemy a povrchy dalších typů jehlanů
ČTYŘSTĚN
Z herního světa je známá Rubikova kostka ve tvaru krychle, ale rovněž existuje atypická Rubikova kostka ve tvaru pravidelného trojbokého jehlanu (pravidelného čtyřstěnu), zvaná Pyraminx, vyobrazená na obr. 4.8.1.

Obrázek 4.8.1: Atypická Rubikova kostka (Pyraminx) ve tvaru pravidelného čtyřstěnu [35]
Poznámka
Nezapomínejme, že existují i pravidelné trojboké jehlany, které ale nejsou pravidelnými čtyřstěny. Ovšem všechny trojboké jehlany můžeme nazývat čtyřstěny.
Příklad 4.8.1
Vypočítejte objem V čtyřstěnu CDEF. Jeho podstava je rovnostranný trojúhelník CDE o straně 8 mm a délka jeho tělesové výšky v je v = 10 mm. Výsledek zaokrouhlete na dvě desetinná místa.
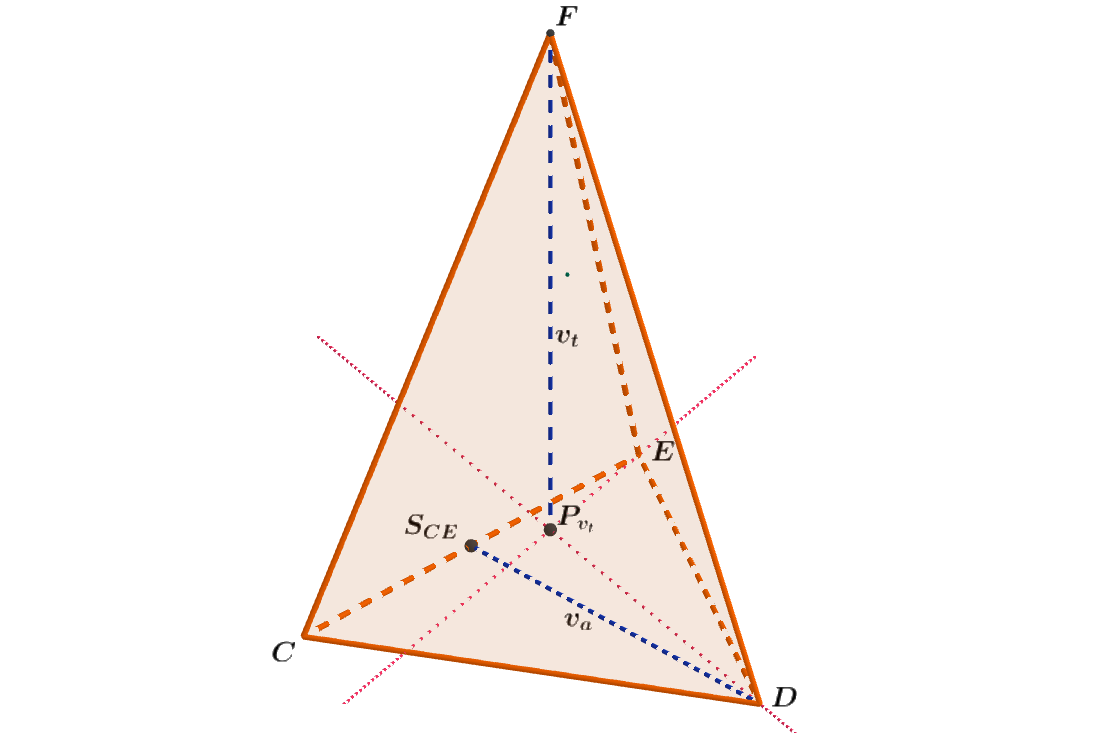
Obrázek 4.8.2: Ilustrace Příkladu 4.8.1
Řešení
- Pro objem V jehlanu platí V = \frac{1}{3} S_pv. Potřebujeme znát obsah podstavy S_p, délku tělesové výšky v známe v = |P_{V}F| = 10 mm.
- Body S_{CD}, S_{CE} jsou středy příslušných stran trojúhelníku (obr. 4.8.2).
- Obsah podstavy S_p je roven obsahu rovnostranného trojúhelníku o straně a = 8 mm. Pro obsah trojúhelníku platí S_{\triangle CDE} = \frac{a \cdot v_a}{2}.
- Pro délku stěnové výšky v_a této podstavy platí v_a=a\frac{\sqrt3}{2}. Tuto hodnotu určíme pomocí Pýthagorovy věty z pravoúhlého \triangle S_{CE}DC; v_a = 8\frac{\sqrt3}{2} mm.
- Pro obsah podstavy S_p platí S_p = S_{\triangle CDE} = \frac{a \cdot v_a}{2} = \frac{8\ \cdot\ 8\frac{\sqrt3}{2}}{2} mm^2 = 16\sqrt3 mm^2.
- Pro objem V jehlanu platí V = \frac{1}{3}S_pv = \frac{1}{3}\ \cdot\ 16\sqrt3\ \cdot\ 10 mm^3 = \frac{160}{3} \sqrt3 mm^3 \doteq 92,38 mm^3.
- Objem čtyřstěnu CDEF je po zaokrouhlení 92,38 mm^3.
Příklad 4.8.2
Povrch pravidelného čtyřstěnu UVWZ o hraně a=5 m je \frac {50 \sqrt3 }{2} m^2. Určete jeho objem V. Výsledek zaokrouhlete na dvě desetinná místa.
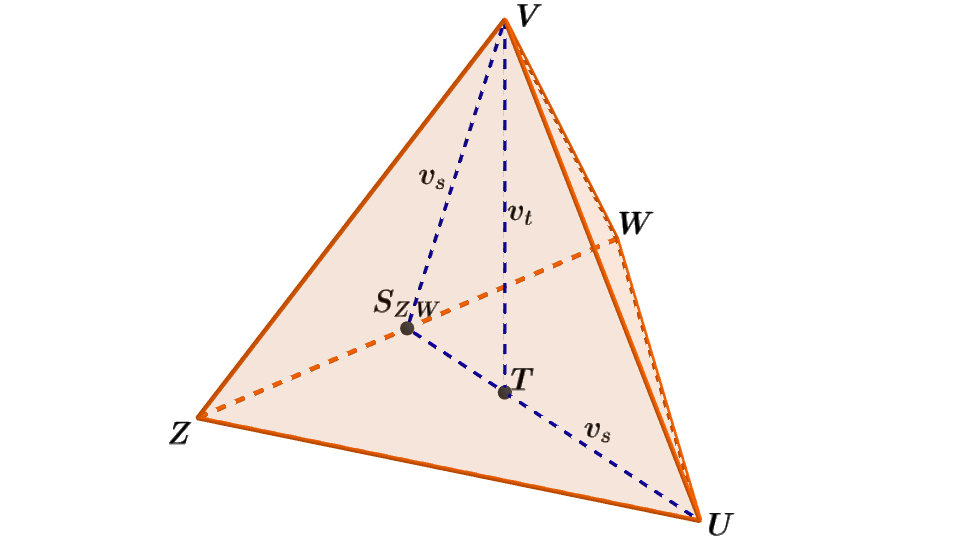
Obrázek 4.8.3: Ilustrace Příkladu 4.8.2
Řešení
- Jelikož je čtyřstěn pravidelný, všechny jeho stěny včetně podstavy tvoří shodné rovnostranné trojúhelníky o straně a. Pro výpočet objemu čtyřstěnu potřebujeme znát obsah podstavy S_p a délku tělesové výšky v_t (obr. 4.8.3).
- Pro povrch S jehlanu platí S = S_p+S_{pl} = \frac {50 \sqrt3 }{2} m^2.
- Povrch čtyřstěnu je tvořen čtyřmi shodnými rovnostrannými trojúhelníky, tudíž platí:
S_p= \frac{S}{4} = \frac{50 \frac{\sqrt3}{2}}{4} m^2 = \frac {25\sqrt3}{4} m^2. - Víme, že v_t = |TV|, neboť bod T je patou tělesové výšky čtyřstěnu a současně je těžištěm trojúhelníku ZUW. Vycházíme například z rovnoramenného \triangle UVS_{ZW}. Vyjádříme délku jeho stran: |VU| = 5 cm; |US_{ZW}| = |VS_{ZW}| = v_s.
- Pro délku stěnové výšky v_s každé boční stěny platí v_s=a\frac{\sqrt3}{2}. Tuto hodnotu vypočítáme Pýthagorovou větou například z rovnostranného \triangle ZUW, který rozdělíme pomocí v_s na dva pravoúhlé trojúhelníky.
- Víme, že TV je výška trojúhelníku UVS_{ZW}, která je kolmá k US_{ZW}. US_{ZW} je zárověň těžnice \triangle ZUW. Z čehož vyplývá, že |TU| = \frac{2}{3} |US_{ZW}| = \frac{2}{3} v_s = \frac{2}{3} a\frac{\sqrt3}{2} = \frac{a\sqrt3}{3} = \frac{5\sqrt3}{3} m.
- Z pravoúhlého \triangle TUV vyjádříme v_t pomocí Pýthagorovy věty; v_t = \sqrt{(a^2 - (\frac{a\sqrt3}{3})^2)} = \sqrt{(25 - (\frac{5\sqrt3}{3})^2)} m = \sqrt{\frac{50}{3}} m = 5\sqrt{\frac{2}{3}} m.
- Pro objem V jehlanu platí: V = \frac{1}{3}S_pv_t = \frac{1}{3}\ \cdot\ \frac {25\sqrt3}{4}\ \cdot\ 5\sqrt{\frac{2}{3}} m^3 = \frac{125\sqrt{2}}{12} m^3 \doteq 14,73 m^3.
- Objem pravidelného čtyřstěnu UVWZ je po zaokrouhlení 14,73 m^3.
KOMOLÝ JEHLAN
Pro odvození vzorce pro objem komolého jehlanu vezmeme komolý jehlan A_1A_2...A_nA^1_1A^2_2...A^1_n s tělesovou výškou v, který doplníme o jehlan A^1_1A^1_2...A^1_nV s tělesovou výškou v_2 na jehlan A_1A_2...A_nV s tělesovou výškou v_1 (obr.4.2.4).
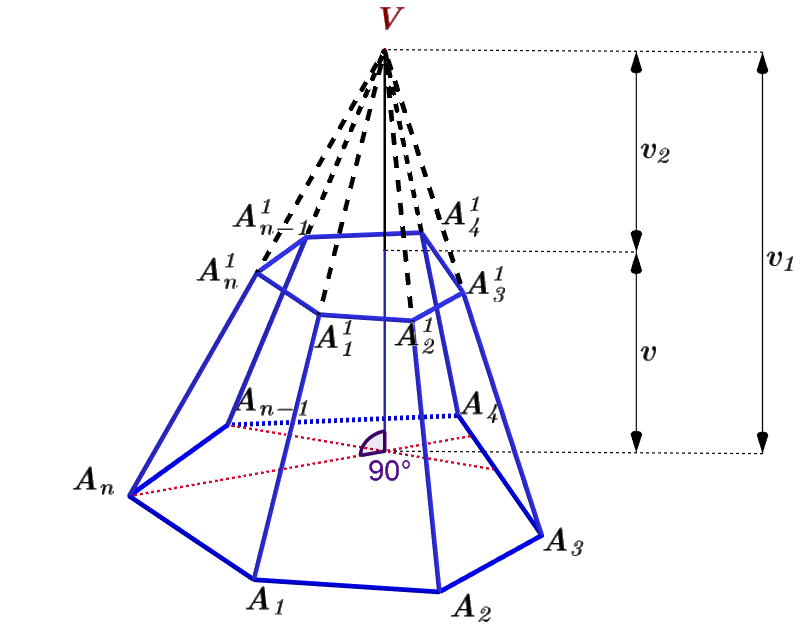
Obrázek 4.8.4: Komolý jehlan
Pro objemy V_1, V_2 jehlanů s výškami v_1, v_2 a pro objem V komolého jehlanu platí
V_1 = V + V_2, tj. V = V_1 - V_2.
Jsou-li S_1 a S_2 obsahy podstav komolého jehlanu, platí
V=\frac{1}{3}S_1v_1 - \frac{1}{3}S_2v_2.
Jelikož v_1 = v + v_2 dostáváme
V=\frac{1}{3}S_1(v + v_2) - \frac{1}{3}S_2v_2
čili
V=\frac{1}{3}S_1v + \frac{1}{3}(S_1 - S_2)v_2.
Podstavy komolého jehlanu jsou podobné mnohoúhelníky, z čehož vyplývá, že koeficient podobnosti k je

k=\frac{v_2}{v_1}
a pro obsahy podstav komolého jehlanu platí
\frac{S_2}{S_1}=k^2; tedy k=\frac{\sqrt{S_2}}{\sqrt{S_1}}.
Tudíž
\frac{v_2}{v_1}=\frac{\sqrt{S_2}}{\sqrt{S_1}}.
Postupnými úpravami dostáváme (pro v_1=v+v_2)
v_2=\frac{\sqrt{S_2}}{\sqrt{S_1}-\sqrt{S_2}}v.
Dostáváme V komolého jehlanu:
V=\frac{1}{3}S_1v + \frac{1}{3}(S_1 - S_2)\frac{\sqrt{S_2}}{\sqrt{S_1}-\sqrt{S_2}}v.
Rozdíl S_1 - S_2 rozložíme na součin (\sqrt{S_1}-\sqrt{S_2})(\sqrt{S_1}+\sqrt{S_2}) a upravíme na výsledný tvar:
V=\frac{1}{3}(S_1 + \sqrt{S_1S_2} + S_2)v.
Předchozí úvahy můžeme nyní shrnout.
Objem V komolého jehlanu s tělesovou výškou v, jehož podstavy mají obsah S_1, S_2, je
V=\frac{1}{3}(S_1 + \sqrt{S_1S_2} + S_2)v.
Dále si uvedeme vztah pro povrch komolého jehlanu:
Pro povrch S komolého jehlanu platí
S=S_1 + S_2 + S_{pl},
kde S_1, S_2 jsou obsahy podstav a S_{pl} je obsah pláště.
Následující vysvětlení způsobu určení objemu pravidelného komolého jehlanu vychází z [2b, s. 97–99]. K objemu pravidelného komolého jehlanu pravděpodobně dospěli již staří Egypťané. Na moskevském papyrusu se nachází úloha na výpočet pravidelné komolé pyramidy, tedy pravidelného komolého čtyřbokého jehlanu (obr. 4.8.5).
Obrázek 4.8.5: Applet – Ilustrace k odvození vzorce pro objem komolého jehlanu
Uvažujme pravidelný komolý čtyřboký jehlan o podstavných hranách a, b a výšce h. Toto těleso rozložíme na devět částí: jeden pravidelný čtyřboký hranol výšky h o podstavné hraně délky b; čtyři jehlany výšky h s čtvercovou podstavou o hraně (\frac{a-b}{2}); a čtyři shodné trojboké hranoly, každý z nich má objem rovný polovině objemu kvádru výšky h a o rozměrech podstavy b, \frac{a-b}{2}. Pokud sečteme objemy dílčích těles z obr. 4.8.5, dostáváme se k následujícímu vztahu:
V=b^2h + 4 \cdot \frac{1}{3} \cdot (\frac{a-b}{2})^2 \cdot h + 4 \cdot \frac{1}{2} \cdot b \cdot \frac{a-b}{2} \cdot h =\frac{h}{3} \cdot (a^2+ab+b^2),
který odpovídá vzorci pro objem komolého jehlanu, jelikož \frac{h}{3} = \frac{1}{3} \cdot h, kde h = v; dále a^2 = S_1; ab = \sqrt{S_1S_2} a b^2 = S_2, kde S_1, S_2 jsou obsahy podstav komolého jehlanu.
Příklad 4.8.3
Určete tělesovou výšku v pravidelného komolého čtyřbokého jehlanu KLMNOPQR, jehož dolní podstava má stranu délky a_1 = 8 dm a horní podstava má stranu délky a_2 = 6 dm. Objem V tohoto komolého jehlanu je 271,3 dm^3. Výsledek zaokrouhlete na jedno desetinné místo.
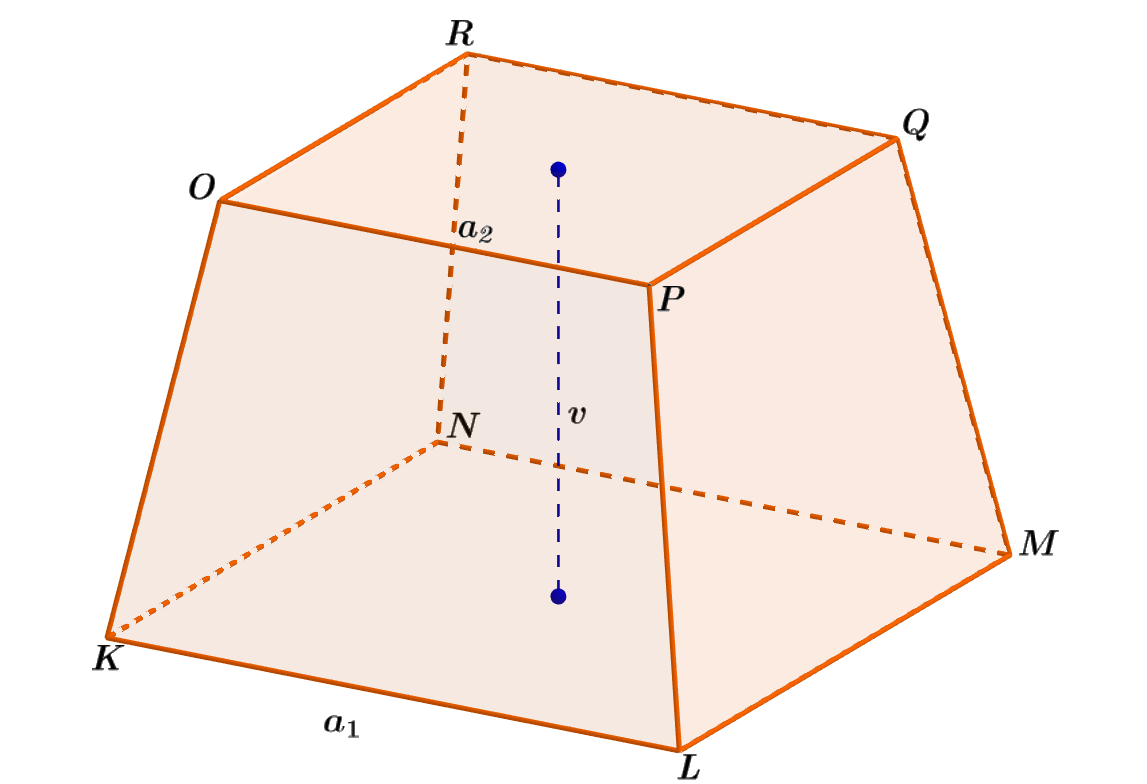
Obrázek 4.8.6: Ilustrace Příkladu 4.8.3
Řešení
- Pro výpočet objemu komolého jehlanu s obsahy podstav S_1, S_2 a výšce v použijeme vzorec V=\frac{1}{3}(S_1 + \sqrt{S_1S_2} + S_2)v.
- Jedná se o pravidelný komolý čtyřboký jehlan, jeho podstavy jsou čtverce. Délka strany čtverce tvořícího dolní podstavu je a_1=8 dm; obsah této podstavy je S_1 = {a_1}^2 = 64 dm^2(obr. 4.8.6).
- Délka strany čtverce tvořící horní podstavu je a_2 = 6 dm; obsah této podstavy je S_1 = {a_2}^2 = 36 dm^2.
- Ze vzorce pro objem V komolého jehlanu vyjádříme neznámou v, přičemž S_1, S_2 již známe; v=\frac{3V}{(S_1 + \sqrt{S_1S_2} + S_2)} a dosadíme obsahy podstav; v=\frac{3V}{(S_1 + \sqrt{S_1S_2} + S_2)} = \frac{3 \cdot 271,3}{(64\ +\ \sqrt{64.36}\ +\ 36)} dm \doteq 5,5 dm.
- Tělesová výška v po zaokrouhlení činí 5,5 dm.
