Objem hranolu
V této kapitole si představíme, jak se počítá objem hranolu. Při odvození vzorce pro objem hranolu vycházíme ze vzorce pro objem kvádru o hranách délky a, b, c, který známe ze základní školy. Na základní škole kvádr rozřezáme na krychličky s hranou jednotkové délky. Krychlička s hranou jednotkové délky má jednotkový objem. Potom objem kvádru odpovídá počtu krychliček vynásobenému (jednotkovým) objemem krychličky.
Tedy objem V kvádru o rozměrech a, b, c je
V =abc.
Na následujícím appletu (obr. 3.6.1) je dostupná animace ilustrující vztah mezi rozměry kvádru a, b, c v centimetrech a jeho objemem. Délka hrany jednotkové krychle v appletu je 1 cm. Animaci lze zastavit kliknutím na tlačítko v levém dolním rohu appletu a poté ovládat posuvníky (délka, šířka, výška) ručně.
Obrázek 3.6.1: Applet – objem kvádru je roven celkovému počtu jednotkových krychlí
Odvození vzorce pro objem n-bokého hranolu
Nejdříve odvodíme vzorec pro konvexní kolmé hranoly, potom pro konvexní kosé hranoly a nakonec platnost vztahu pro objem hranolu zobecníme na libovolný nekonvexní hranol.
Kvádr o podstavných hranách délky a,b můžeme rozříznout rovinou kolmou k podstavám a obsahující tělesovou úhlopříčku na dva shodné kolmé trojboké hranoly, které mají za podstavy pravoúhlé trojúhelníky (obr. 3.6.2). Podle první vlastnosti objemu se jejich objemy rovnají a podle druhé vlastnosti objemu objem kvádru dostaneme součtem objemů obou kolmých trojbokých hranolů. Tedy objem V kolmého trojbokého hranolu, jehož podstavy jsou shodné pravoúhlé trojúhelníky, je roven polovině objemu původního kvádru.
Obrázek 3.6.2: Applet – kvádr rozdělený na dva kolmé trojboké hranoly
Z předchozího tvrzení vyplývá, že pokud jsou rozměry původního kvádru a, b, c, pak pro objem V dílčího kolmého trojbokého hranolu, jehož podstavy jsou pravoúhlé trojúhelníky, platí
V=\frac12abc =(\frac12ab)c.
Výraz \frac12ab určuje obsah trojúhelníkové podstavy, označíme ho S_p, výška hranolu v=c. Pro objem kolmého trojbokého hranolu, jehož podstava je pravoúhlý trojúhelník, platí
V = S_p v.
V případě, že podstavou kolmého trojbokého hranolu je obecný trojúhelník, víme, že nejvýše jeden jeho vnitřní úhel je tupý. Díky tomu lze trojúhelník vždy rozdělit jednou jeho výškou na dva pravoúhlé trojúhelníky. Víme tedy, že lze rozdělit každý kolmý trojboký hranol, jehož podstavy nejsou pravoúhlé trojúhelníky, na dva kolmé trojboké hranoly stejné výšky, jejichž podstavy p_1, p_2 jsou pravoúhlé trojúhelníky (obr. 3.6.3).
Obrázek 3.6.3: Applet – kolmý trojboký hranol rozdělený na dva kolmé trojboké hranoly
Označme V_1 a V_2 jejich objemy, S_{p_1} a S_{p_2} obsahy jejich podstav. Potom pro obsah podstavy S_p daného hranolu platí S_p = (S_{p_1} + S_{p_2}) . Oba dílčí kolmé trojboké hranoly mají stejné výšky jako daný hranol. Podle druhé vlastnosti objemu je objem daného hranolu
V = V_1 + V_2 = S_{p_1}v + S_{p_2}v = (S_{p_1} + S_{p_2})v = S_pv.
Konvexní kolmý n-boký hranol jsme schopni rozložit na n kolmých trojbokých hranolů se stejnou výškou v (obr. 3.6.4). Součet obsahů S_{p_1}, S_{p_2}, ... , S_{p_n} jejich podstav se rovná obsahu S_{p} podstavy daného hranolu a výšky jsou stejné. Podle druhé vlastnosti objemu je objem daného hranolu
V = V_1 + V_2 +...+ V_n = S_{p_1}v + S_{p_2}v +...+ S_{p_n}v = (S_{p_1} + S_{p_2} +...+ S_{p_n})v = S_pv.
Obrázek 3.6.4: Applet – kolmý hranol rozdělený na n kolmých trojbokých hranolů
Pomocí Cavalieriho principu lze dokázat platnost stejného vzorce i pro objem libovolného kosého hranolu. Uvažujme kolmý a kosý hranol o stejné výšce, jejichž podstavy leží ve stejné rovině a mají stejný obsah. Řezy kolmým i kosým hranolem vedené rovnoběžně s rovinou jejich podstav v libovolné výšce jsou vždy shodné s podstavou, protože rovina řezu je s ní rovnoběžná; obsahy řezu kolmého i kosého hranolu jsou shodné. Tudíž objemy těchto hranolů jsou si rovny. Na appletu (obr. 3.6.5) se nachází kolmý čtyřboký hranol s podstavou ve tvaru čtverce o straně a a kosý čtyřboký hranol s podstavou ve tvaru obdélníku o stranách b,c, jejichž podstavy mají stejný obsah (veličiny jsou uvedeny bez jednotek). Změnou polohy bodu H měníme vzdálenost roviny řezu a podstavy, změnou polohy vrcholu A_1" měníme výšku obou hranolů. Můžeme pozorovat, že změnami poloh těchto bodů se obsahy řezů hranolů nemění.
Obrázek 3.6.5: Applet – využití Cavalieriho principu pro kolmý a kosý hranol se stejnými obsahy podstav S_p a se stejnými výškami v
S využitím Cavalieriho principu lze rovněž dokázat platnost stejného vzorce i pro objem libovolného nekonvexního hranolu. Uvažujme konvexní a nekonvexní hranol o stejné výšce, jejichž podstavy leží ve stejné rovině a mají stejný obsah. Řezy konvexním i nekonvexním hranolem vedené rovnoběžně s rovinou jejich podstav v libovolné výšce jsou vždy shodné s podstavou, protože rovina řezu je s ní rovnoběžná; obsahy řezu konvexního i nekonvexního hranolu jsou shodné. Tudíž objemy těchto hranolů jsou si rovny. Na appletu (obr. 3.6.6) se nachází konvexní čtyřboký hranol a nekonvexní pětiboký hranol, jejichž podstavy mají stejný obsah (veličiny jsou uvedeny bez jednotek). Změnou polohy bodu H měníme vzdálenost roviny řezu a podstavy, změnou polohy vrcholu A_1" měníme výšku obou hranolů. Můžeme pozorovat, že změnami poloh těchto bodů se obsahy řezů hranolů nemění.
Obrázek 3.6.6: Applet – využití Cavalieriho principu pro konvexní a nekonvexní hranol se stejnými obsahy podstav S_p a se stejnými výškami v
Předchozí úvahy můžeme nyní shrnout.
Objem V libovolného hranolu vypočítáme tak, že obsah podstavy S_p vynásobíme jeho výškou v, platí
V = S_p v.
Příklad 3.6.1
Vypočítejte objem V pravidelného pětibokého hranolu ABCDEFGHIJ. Jeho boční stěny jsou tvořeny shodnými čtverci o straně délky a = 5 cm. Výsledek zaokrouhlete na dvě desetinná místa.
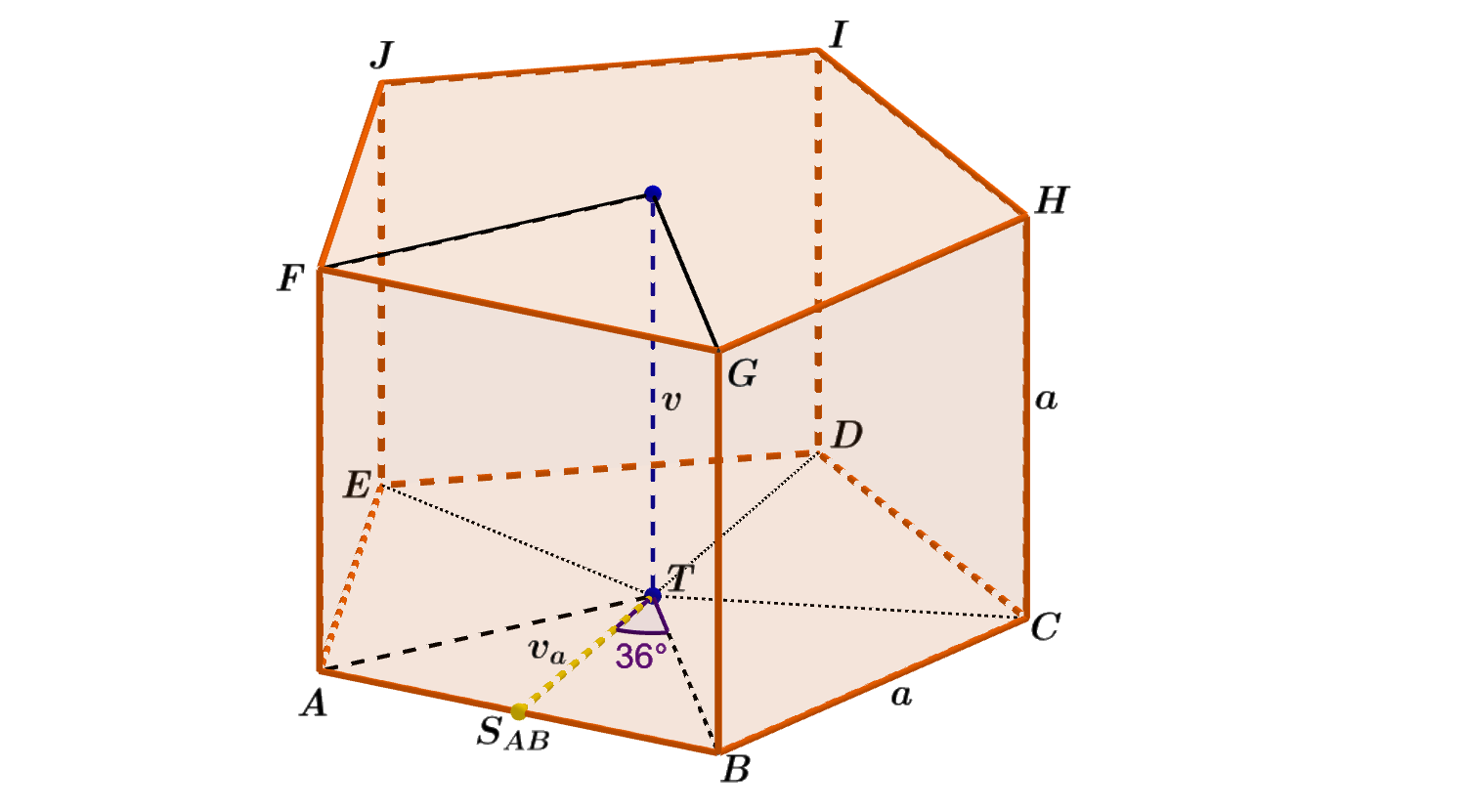
Obrázek 3.6.6: Ilustrace Příkladu 3.6.1
Řešení
- Pro objem V hranolu platí V = S_p v, tedy potřebujeme znát obsah podstavy S_p a jeho výšku v.
- Podstavami hranolu ABCDEFGHIJ jsou pravidelné pětiúhelníky o straně a=5 cm. Pravidelný pětiúhelník rozložíme na pět shodných rovnoramenných trojúhelníků (obr. 3.6.6); S_{\triangle ABT} = \frac{a v_a}{2}.
Z \triangle AS_{AB}T vyjádříme v_a; v_a = \cot 36° \cdot \frac {a}{2} \doteq 1,376 \cdot 2,5 cm \doteq 3,441 cm.
Tedy S_{\triangle ABT} = \frac{5\ \cdot\ 3,441}{2} cm^2 \doteq 8,603 cm^2. - Pro obsah podstavy S_p platí: S_p = 5 \cdot S_{\triangle ABT} = 5 \cdot 8,603 cm^2 \doteq 43,015 cm^2.
- Jelikož jsou boční stěny pravidelného pětibokého hranolu tvořeny shodnými čtverci, tak tělesová výška v má stejnou velikost jako podstavná hrana; v = a = 5 cm.
- Pro objem hranolu platí: V = S_pv = 43,015 \cdot 5 cm^3 \doteq 215,08 cm^3.
- Objem pravidelného pětibokého hranolu ABCDEFGHIJ je po zaokrouhlení 215,08 cm^3.
Příklad 3.6.2
Je dán kosý šestiboký hranol GHIJKLMNOPQR, jehož podstavy jsou pravidelné šestiúhelníky o straně a = 4 dm. Jeho tělesová výška v_t = 6 dm. Jaký je objem V tohoto hranolu? Výsledek zaokrouhlete na dvě desetinná místa.
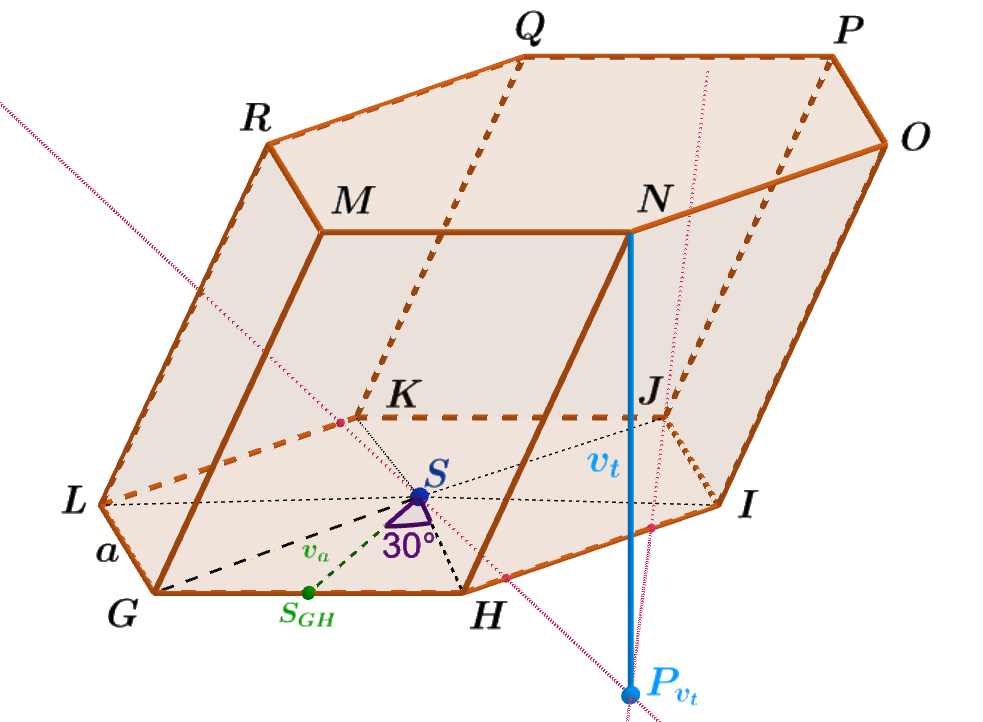
Obrázek 3.6.7: Ilustrace Příkladu 3.6.2
Řešení
- Pro objem V hranolu platí V = S_p v, tedy potřebujeme znát obsah podstavy S_p a jeho výšku v_t.
- Podstavami hranolu GHIJKLMNOPQR jsou pravidelné šestiúhelníky o straně a=6 dm. Pravidelný šestiúhelník rozložíme na šest shodných rovnostranných trojúhelníků (obr. 3.6.7); S_{\triangle GHS} = \frac{a v_a}{2}. Z \triangle S_{GH}HS vyjádříme v_a; v_a = \cot 30° \cdot \frac {a}{2} \doteq 1,732 \cdot 2 dm \doteq 3,464 dm. Tedy S_{\triangle GHS} = \frac{4\ \cdot\ 3,464}{2} dm^2 \doteq 6,928 dm^2.
- Pro obsah podstavy S_p platí: S_p = 6 \cdot S_{\triangle GHS} = 6 \cdot 6,928 dm^2 \doteq 41,892 dm^2.
- Tělesová výška v_t = |P_{v_t}N| = 6 dm.
- Pro objem hranolu platí: V = S_pv_t = 41,892 \cdot 6 dm^3 \doteq 251,35 dm^3.
- Objem kosého šestibokého hranolu GHIJKLMNOPQR je po zaokrouhlení 251,35 dm^3.
Příklad 3.6.3
Je dán kolmý čtyřboký hranol RTUVWXYZ, jehož podstavou je rovnoramenný lichoběžník o základnách délky a = 8 m a c = 4,5 m. Výška v_p lichoběžníku je 4 m, pro tělesovou výšku hranolu platí v_t = 5 m. Vypočítejte objem V tohoto hranolu.
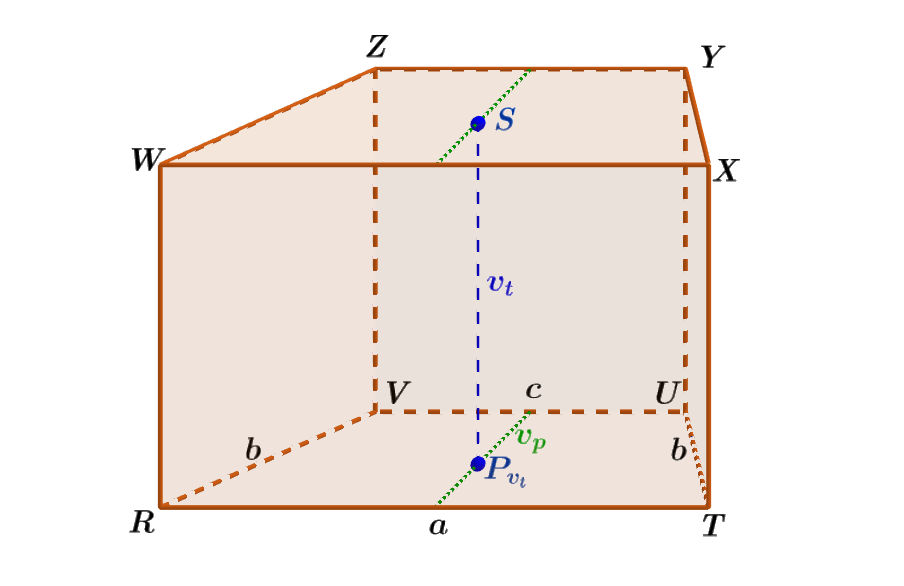
Obrázek 3.6.8: Ilustrace Příkladu 3.6.3
Řešení
- Pro objem V hranolu platí V = S_p v, tedy potřebujeme znát obsah podstavy S_p a jeho výšku v_t.
- Podstavami hranolu RTUVWXYZ jsou shodné rovnoramenné lichoběžníky o základnách délky a = 8 m a c = 4,5 m (obr. 3.6.8). Vypočítáme obsah S_p jedné podstavy, tedy obsah rovnoramenného lichoběžníku; S_p = S_{RTUV} = \frac{(a\ +\ c)\ \cdot\ v_p}{2} = \frac{(8\ +\ 4,5)\ \cdot\ 4}{2} m^2 = 25 m^2.
- Pro objem hranolu platí: V = S_pv = 25 \cdot 5 m^3 = 125 m^3.
- Objem kolmého čtyřbokého hranolu RTUVWXYZ je 125 m^3.
Příklad 3.6.4
Vyjádřete objem nekonvexního pětibokého kolmého hranolu A_1A_2S_1A_3A_4A_5A_6S_2A_7A_8, který vznikl z pravidelného čtyřbokého hranolu A_1A_2A_3A_4A_5A_6A_7A_8 o podstavné hraně a a výšce v odseknutím kolmého trojbokého hranolu o stejné výšce v, jehož dolní podstavou je \triangle A_2A_3S_1, kde S_1 je střed čtvecové podstavy A_1A_2A_3A_4.
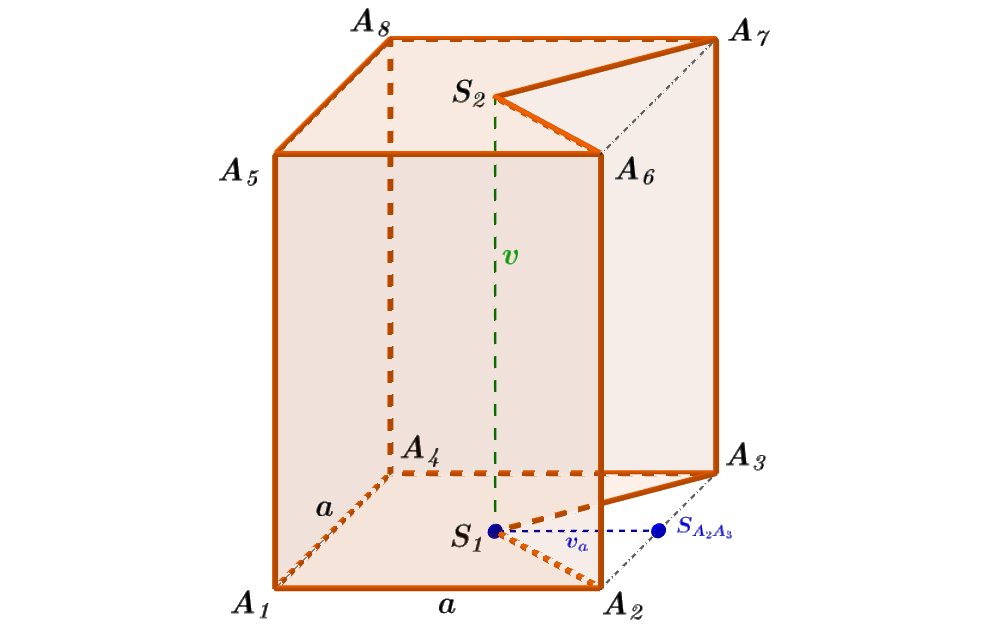
Obrázek 3.6.9: Ilustrace Příkladu 3.6.4
Řešení
- Pro objem V hranolu platí V = S_p v, tedy potřebujeme znát obsah podstavy S_p a jeho výšku v.
- Podstavami hranolu A_1A_2S_1A_3A_4A_5A_6S_2A_7A_8 jsou shodné nekonvexní pětiúhelníky vzniklé ze čtverce A_1A_2A_3A_4 odseknutím rovnoramenného \triangle A_2A_3S_1 s výškou v_a = \frac {a}{2} (obr. 3.6.9). Vyjádříme obsah S_p jedné podstavy, tedy obsah nekonvexního pětiúhelníku A_1A_2S_1A_3A_4; S_p = a^2 - \frac{a\ \cdot\ v_a}{2} = a^2 - \frac{a\ \cdot\ \frac{a}{2}}{2} = a^2 - \frac{a^2}{4} = \frac{3a^2}{4}.
- Pro objem hranolu platí: V = S_pv = \frac{3 a^2 v}{4}.
- Objem kolmého čtyřbokého hranolu A_1A_2S_1A_3A_4A_5A_6S_2A_7A_8 je \frac{3 a^2 v}{4}.
