Nezapomeňte, že násobení vektoru skalárem musíte provést před sčítáním vektorů.
Násobení vektorů reálným číslem
Násobek nulového vektoru reálným číslem k je nulový vektor.
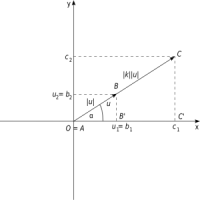
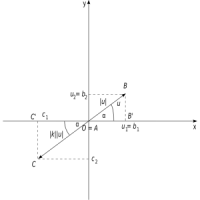
Násobek nenulového vektoru u = B - A reálným číslem k je vektor v = C - A, přičemž C je bod, pro který platí
- |AC| = |k|·|AB|
- Je-li k ≥ 0, leží bod C na polopřímce AB; je-li k < 0, leží bod C na polopřímce opačné k polopřímce AB.
Násobení vektoru u číslem k zapisujeme v = ku.
Násobení vektoru skalárem (reálným číslem) lze geometricky reprezentovat jeho prodloužením nebo zkrácením, popřípadě změnou jeho orientace na opačnou (při násobení záporným číslem). Pro nás je důležité, jak násobení vektoru číslem vyjádříme v souřadnicích v rovině a v prostoru.
Pro každý vektor u = (u1; u2) v rovině a každé reálné číslo k platí ku = (ku1; ku2).
Pro každý vektor u = (u1; u2; u3) v prostoru a každé reálné číslo k platí ku = (ku1; ku2; ku3).
Vypočítejte souřadnice vektoru u = v + 2w, kde v = (2; 1; -3) a w = (2; 3;1).
- u = (2; 1; -3) + 2(2; 3; 1),
- u = (2; 1; -3) + (4; 6; 2),
- u = (6; 7; -1).
Umět sčítat vektory a násobit je reálným číslem nám stačí k tomu, abychom si zavedli velmi důležitý pojem.
Mějme vektory u, v, w, které jsou všechny buď v rovině, nebo v prostoru. Vektor z = au + bv + cw, kde a, b, c ∈ ![]() , se nazývá lineární kombinace vektorů u, v, w.
, se nazývá lineární kombinace vektorů u, v, w.
Lze utvořit lineární kombinaci i dvou, čtyř, pěti atd. vektorů. Lineární kombinace jednoho vektoru je jeho reálný k-násobek.
Určete, zda vektor w = (5; 4) je lineární kombinací vektorů u = (1; 2) a v = (2; 1).
- Aby náš zadaný vektor w byl lineární kombinací vektorů u a v, musel by splňovat následující podmínku: w = au + bv, pro nějaká a, b ∈
 . Protože vektory jsou si rovny, pokud se rovnají jejich souřadnice, hledáme reálná čísla a a b taková, aby platilo (5; 4) = a(1; 2) + b(2; 1). Tedy
. Protože vektory jsou si rovny, pokud se rovnají jejich souřadnice, hledáme reálná čísla a a b taková, aby platilo (5; 4) = a(1; 2) + b(2; 1). Tedy
5 = a + 2b,
4 = 2a + b.
- Chceme najít řešení výše uvedené soustavy dvou rovnic o dvou neznámých. Z druhé rovnice vyjádříme b = 4 - 2a a získáme
5 = a + 8 - 4a.
- Z toho jednoduše dostaneme řešení soustavy a = 1 a b = 2.
- Soustava má řešení, proto je vektor w lineární kombinací vektorů u a v a platí w = u + 2v. To znamená, že jej získáme součtem vektoru u s dvojnásobkem vektoru v. Podívejte se na obr. 2.4.
-
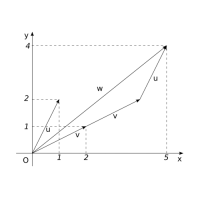 Obr. 2.4: Lineární kombinace vektorů
Obr. 2.4: Lineární kombinace vektorů
Určete, zda je vektor w = (4; 5) je lineární kombinací vektorů u = (2; -1) a v = (-4; 2).
- Podobně jako v předcházejícím příkladě hledáme reálná čísla a, b taková, aby w = au + bv. Po rozepsání v souřadnicích hledáme řešení rovnic
4 = 2a - 4b,
5 = -a + 2b. - Když k první rovnici přičteme dvojnásobek druhé rovnice, získáme následující rovnost
4 + 10 = 2a - 4b - 2a + 4b,
14 ≠ 0. - Soustava nemá řešení a hledaná a, b neexistují, proto vektor w není lineární kombinací vektorů u a v.
Určete, zda je vektor u = (7; 11; 4) lineární kombinací vektorů v = (2; 1; -1) a w = (1; 3; 2).