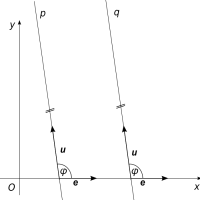
Směrnice přímky p vyjadřuje tangens odchylky φ vektorů e = (1; 0) a u = (u1; u2), kde u je libovolný směrový vektor přímky p, jehož souřadnice u2 > 0.
Směrnicový a úsekový tvar rovnice přímky
Mimo parametrické a obecné rovnice přímky se používají ještě další vyjádření. Jsou to směrnicový a úsekový tvar rovnice přímky. Narozdíl od parametrické a obecné rovnice neumožňují vyjádřit všechny přímky, a proto se až tolik nevyužívají. Je ale důležité je znát a vědět, jaké mají výhody a nevýhody.
Směrnicový tvar rovnice přímky
Jak je vidět z následující definice, směrnicový tvar rovnice přímky je vlastně předpisem funkce proměnné x. Z toho plyne jisté omezení, které si později ukážeme.
Rovnice
y = kx + q; k, q ∈ ![]() ,
,
se nazývá směrnicový tvar rovnice přímky. Číslo k se nazývá směrnice přímky.
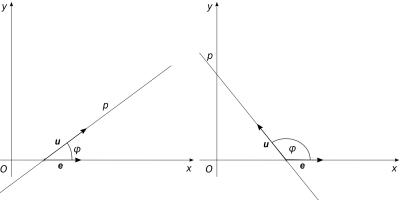
Směrnicový tvar přímky neumožňuje popsat ty přímky, které jsou rovnoběžné s osou y. Protože směrnice vyjadřuje tangens úhlu a tangens 90° není definován, není pro takovou přímku definována ani směrnice, a nemůžeme ji tudíž vyjádřit.
Dvě přímky jsou spolu rovnoběžné právě tehdy, když jsou různoběžné s osou y a jejich směrnice jsou totožné nebo pokud jsou obě rovnoběžné s osou y.
Jestliže dvě přímky mají stejnou směrnici, pak jsou rovnoběžné.
Jestliže přímka p má nenulovou směrnici k a přímka q je na ni kolmá,
pak směrnice přímky q je rovna \(\dfrac{1}{k}\).
Úsekový tvar rovnice přímky
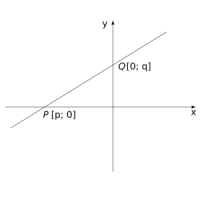
Mějme na souřadnicových osách dány body P[p; 0] a Q[0; q], které jsou různé od počátku. Přímka PQ má potom rovnici:
\(\dfrac{x}{p} + \dfrac{y}{q} = 1\).
Z úsekového tvaru rovnice přímky tedy můžeme velmi jednoduše vyčíst průsečíky přímky se souřadnicovými osami nebo naopak z průsečíků se souřadnicovými osami můžeme snadno zjistit rovnici přímky, která osy v daných bodech protíná.
Rovnici přímky v úsekovém tvaru lze psát právě tehdy, když přímka není rovnoběžná s žádnou souřadnicovou osou a neprochází počátkem.
Je-li to možné, najděte pro přímku AB, kde A[0; 3], B[6; 0] parametrické vyjádření, obecnou rovnici, směrnicový a úsekový tvar její rovnice.
- Směrový vektor přímky AB: u = B - A = (6; -3).
- Normálový vektor přímky AB: n = (3; 6).
- Parametrická rovnice
x = 6t,
y = 3 - 3t; t ∈ .
. - Obecná rovnice
3x + 6y + c = 0,
po dosazení souřadnic bodu A získáme c = -18 a obecná rovnice přímky AB je
3x + 6y - 18 = 0, což můžeme zapsat jako:
x + 2y - 6 = 0. - Směrnicový tvar
y = kx + q,
po dosazení souřadnic bodů A a B do směrnicového tvaru rovnice získáme soustavu dvou rovnic o dvou neznámých:
3 = 0k + q,
0 = 6k + q.
Z první rovnice můžeme vyjádřit q = 3 a dosadit do rovnice druhé. Řešením je potom k = -1/2 a q = 3. Směrnicový tvar rovnice přímky AB vypadá takto:
\(y = \dfrac{-x}{2} + 3\). - Úsekový tvar
Protože ze zadání známe průsečíky se souřadnicovými osami, můžeme úsekový tvar rovnou zapsat jako:
\(\dfrac{x}{6} + \dfrac{y}{3} = 1\).