\begin{align} \end{align}

Kružnice

Kružnice je z kuželoseček nejjednodušší a asi i nejznámější, pokud neuvažujeme ty singulární. Vznikne řezem rotační kuželové plochy rovinou kolmou na osu rotace, která neprochází vrcholem. Jinak se dá kružnice zavést jako množina všech bodů dané vlastnosti.

Obr. 5.3: Kružnice jako řez kuželové plochy rovinou
Obr. 5.3: Kružnice jako řez kuželové plochy rovinou
Definice

Kružnice je množina všech bodů roviny, které mají od daného bodu, středu kružnice, danou vzdálenost, poloměr kružnice.

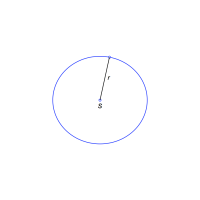
Obr. 5.4: Charakteristiky kružnice
Obr. 5.4: Charakteristiky kružnice
Poznámka

Kružnici s nulovým poloměrem tvoří jediný bod - její střed.

Definice

Rovnice (x - m)2 + (y - n)2 = r2 se nazývá středovou rovnicí kružnice se středem S[m; n] a poloměrem r.

Definice

Rovnice kružnice ve tvaru x2 + y2 - 2mx - 2ny + p = 0, kde p = m2 + n2 - r2, se nazývá obecná rovnice kružnice.

Příklad 5.1

Najděte středovou a obecnou rovnici kružnice se středem S[3; 5] a poloměrem r = 2.

Řešení
  • Středovou rovnici můžeme zapsat přímo podle definice:
    (x - 3)2 + (y - 5)2 = 22.
  • Obecnou rovnici získáme rozepsáním mocnin:
    x2 - 6x + 9 + y2 - 10y + 25 = 4,
    x2 - 6x + y2 - 10y + 30 = 0.
Poznámka

Ne každá rovnice ve tvaru x2 + y2 - 2mx - 2ny + p = 0 je rovnicí kružnice.
Pokud v rovnici doplníme výrazy x2 - 2mx a y2 - 2ny na druhé mocniny dvojčlenů, můžeme ji vyjádřit jako (x - m)2 - m2 + (y - n)2 - n2 + p = 0. To je po úpravě
(x - m)2 + (y - n)2 = m2 + n2 - p.

Je vidět, že o kružnici se jedná jen v případě, že p ≥ m2 + n2.
Pokud je p = m2 + n2, rovnici splňují souřadnice jediného bodu, tj. kružnice má nulový poloměr.
Je-li p < m2 + n2, rovnice nemá žádné řešení, tj. rovnici nevyhovuje žádný bod.

Příklad 5.2

Určete střed a poloměr kružnice dané rovnicí x2 - 2x + y2 + 4y - 11 = 0.

Řešení
  • Doplníme výrazy x2 - 2x a y2 + 4y na druhé mocniny dvojčlenů x - 1 a y + 2:
    x2 - 2x + 1 + y2 + 4y + 4 - 1 - 4 - 11 = 0,
    (x - 1)2 + (y + 2)2 - 16 = 0,
    (x - 1)2 + (y + 2)2 = 16.
  • Střed zadané kružnice je bod S[1; -2] a její poloměr r = 4.
Příklad 5.3

Zjistěte, zda body A[2; 1], B[2; 5], C[4; 5] a D[-1; 2] leží na stejné kružnici.

Řešení
  • Hledaná kružnice se středem S[m; n] a poloměrem r má středovou rovnici:
    (x - m)2 + (y - n)2 = r2.
  • Tři nekolineární body napoveda jednoznačně určují kružnici. My využijeme souřadnic bodů A, B, C, které nekolineární jsou a dosadíme je do obecné rovnice hledané kružnice. Získáme tři rovnice o třech neznámých:
    (2 - m)2 + (1 - n)2 = r2,
    (2 - m)2 + (5 - n)2 = r2,
    (4 - m)2 + (5 - n)2 = r2.
  • Z první a druhé rovnice vyjádříme hodnotu neznámé n:
    (2 - m)2 + (1 - n)2 = (2 - m)2 + (5 - n)2,
    (1 - n)2 = (5 - n)2,
    1 - 2n + n2 = 25 - 10n + n2,
    n = 3.
  • Obdobným způsobem z druhé a třetí rovnice můžeme vyjádřit m = 3. Dosadíme-li získané hodnoty m a n zpět do první rovnice, dopočítáme r2 = 5. Středová rovnice kružnice, určené body A, B a C, je:
    (x - 3)2 + (y - 3)2 = 5.
  • Můžeme si to ověřit dosazením souřadnic bodů A, B, C do této rovnice - vždy musí být splněna. Zkusíme-li dosadit souřadnice bodu D, zjistíme, že získaná rovnost neplatí:
    (-1 - 3)2 + (2 - 3)2 = 5,
    17 ≠ 5.
  • To znamená, že bod D neleží na stejné kružnici jako body A, B a C.
Příklad 5.4

Vypočítejte vzdálenost bodu X[1; 6] od středu kružnice x2 - 4x + y2 - 2y + 10 = 0.

Řešení
  • Nejsnadněji souřadnice středu kružnice zjistíme z její středové rovnice. Budeme proto postupovat podobně jako v příkladě 5.2.
  • x2 - 4x + 4 + y2 - 2y + 1 - 4 - 1 + 10 = 0,
    (x - 2)2 + (y - 1)2 + 5 = 0,
    (x - 2)2 + (y - 1)2 = -5.
  • Protože levá strana rovnice bude vždy nezáporná a pravá je rovna zápornému číslu, je zřejmé, že rovnice nemá žádné reálné řešení a neurčuje proto kružnici. Vzhledem k tomu, že rovnice neurčuje kružnici, nemá smysl v řešení tohoto příkladu pokračovat.