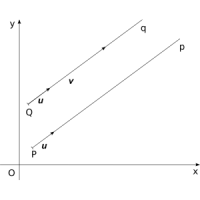
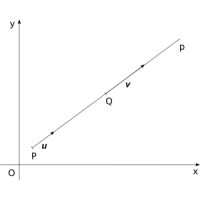
Totožnost přímek je speciální případ rovnoběžnosti. Tj. dvě totožné přímky jsou i rovnoběžné, ale dvě rovnoběžné přímky nemusí být totožné.
Vzájemná poloha přímek
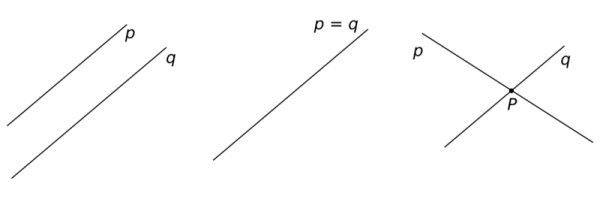
Dvě přímky p, q v rovině mohou mít tři vzájemné polohy viz obr. 3.8.
- p ∩ q = ∅
Přímky p a q jsou rovnoběžné různé. Nemají žádný společný bod. - p ∩ q = {P}
Přímky p a q jsou různoběžné. Mají jeden společný bod, bod P. Zapisujeme p × q. - p ∩ q = p
Přímky p a q jsou totožné. Zapisujeme p = q.
Úmluva: Rovnoběžnost přímek p a q budeme značit jako p || q. Nadále budeme jako rovnoběžné přímky označovat přímky rovnoběžné různé i přímky totožné. Bude-li potřeba polohy rozlišit, použije se příslušný pojem.
Dvě přímky p(P, u) a q(Q, v) jsou rovnoběžné právě tehdy, je-li vektor u nenulovým reálným násobkem vektoru v.
Jsou dány body P[3; 5], Q[2; 1] a vektory u = (1; 2), v = (3; 6). Rozhodněte, zda jsou přímky p(P, u) a q(Q, v) rovnoběžné.
- Hledáme nějaké reálné číslo k takové, aby v = ku (přímky jsou rovnoběžné právě tehdy, je-li vektor v nenulovým násobkem vektoru u). 3 = 1⋅k, 6 = 2k. Pro k = 3 je soustava splněna, přímka p je rovnoběžná s přímkou q.
Dvě přímky p(P, u) a q(Q, v) jsou totožné právě tehdy, jsou-li rovnoběžné a leží-li bod Q na přímce p.
Jsou dány body P[3; 5], Q[2; 1] a vektory u = (1; 2) a v = (3; 6). Rozhodněte, zda jsou přímky p(P, u) a q(Q, v) totožné.
- Ze zadání je vidět, že v = 3u a tedy p || q. Musíme zjistit, zda bod Q leží na přímce p. Přímku p parametricky vyjádříme:
x = 3 + t,
y = 5 + 2t; t ∈ .
.
- Do rovnic dosadíme souřadnice bodu Q a hledáme hodnotu parametru t tak, aby platilo:
2 = 3 + t,
1 = 5 + 2t. - Z první rovnice plyne t = -1. Po dosazení do druhé rovnice získáme 1 = 3. To neplatí a soustava tedy nemá řešení. Bod Q proto neleží na přímce p a přímky p a q jsou rovnoběžné různé.
Jestliže přímky p(P, u), q(Q, v) v rovině nejsou rovnoběžné, jsou různoběžné 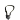 a má smysl hledat jejich průsečík.
Průsečík přímek p, q je bod, který leží na obou přímkách. Je to tedy bod X, pro který platí rovnice:
a má smysl hledat jejich průsečík.
Průsečík přímek p, q je bod, který leží na obou přímkách. Je to tedy bod X, pro který platí rovnice:
X = P + tu,
X = Q + sv, pro nějakou hodnotu parametrů t, s.
Pokud hledáme průsečík těchto přímek, hledáme hodnoty parametrů t a s, pro které obě přímky určují stejný bod. Řešíme tedy rovnici P + tu = Q + sv.
Jsou dány přímky p(P, u) a q(Q, v), P[2; -1], u = (1; 2), Q[0; -2], v = (1; 1). Určete jejich vzájemnou polohu a jsou-li různoběžné, najděte i jejich průsečík
- Nejprve vyloučíme možnost, že by přímky p a q byly rovnoběžné. Je vidět, že směrový vektor u = (1; 2) není násobkem směrového vektoru v = (1; 1), přímky p a q proto nejsou rovnoběžné. Budeme pokračovat tím, že obě přímky vyjádříme parametricky.
-
p:
x = 2 + t,
y = -1 + 2t; t ∈ .
.
q:
x = s,
y = -2 + s; s ∈ .
.
- Hledáme společný bod těchto přímek, tedy bod, jehož x-ová i y-ová souřadnice je v rovnicích obou přímek stejná.
Získáme soustavu dvou rovnic o dvou neznámých:
2 + t = s,
-1 + 2t = -2 + s. -
Řešením soustavy je t = 1 a s = 3. To jsou hodnoty parametrů, které odpovídají souřadnicím námi hledaného průsečíka
přímek p a q v jejich parametrických vyjádřeních.
Stačí buď t = 1 dosadit do parametrické rovnice přímky p nebo s = 3 do parametrické rovnice přímky q a vypočítat souřadnice průsečíku:
p:
x = 2 + 1 = 3,
y = -1 + 2⋅1 = 1.
q:
x = 3,
y = -2 + 3 = 1.
- Přímky p a q jsou různoběžné. Jejich průsečíkem je bod X[3; 1]. Na obr. 3.9 si prohlédněte, jak vypadá situace z tohoto příkladu.
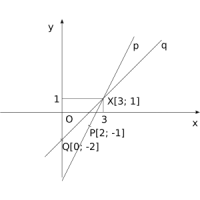 Obr. 3.7: Řešení příkladu 3.10
Obr. 3.7: Řešení příkladu 3.10
Při řešení následujících příkladů si uvědomte, kolik řešení soustavy rovnic s neznámými t, s získáme, pokud bychom postupovali stejně jako v příkladě 3.10, za předpokladu, že p(P, u) a q(Q, v) jsou rovnoběžné různé nebo totožné.
Jsou dány přímky p(P, u) a q(Q, v), P[-1; 0], u = (1; 2), Q[3; 5], u = (3; 6). Určete jejich vzájemnou polohu a jsou-li různoběžné, najděte i jejich průsečík.
p:
x = 1 - t,
y = 2t; t ∈ .
.
q:
x = 3 + 3s,
y = 5 + 6s; s ∈ .
.
- Řešíme soustavu dvou rovnic o dvou neznámých:
-1 + t = 3 + 3s,
2t = 5 + 6s.
Pokud od druhé rovnice odečteme dvojnásobek první získáme
2 = -1. - To neplatí pro žádnou hodnotu t a s a soustava tedy nemá žádné řešení. Tento výsledek geometricky interpretujeme tak, že přímky p a q nemají žádný společný bod, a proto můžeme říci, že přímky p a q jsou rovnoběžné různé.
Jsou dány přímky p(P, u) a q(Q, v), P[1; 2], u = (1; -2), Q[-1; 6], u = (-2; 4). Určete jejich vzájemnou polohu a jsou-li různoběžné, najděte i jejich průsečík.
-
p:
x = 1 + t,
y = 2 - 2t; t ∈ .
.
q:
x = -1 - 2s,
y = 6 + 4s; s ∈ .
.
- Řešíme soustavu dvou rovnic o dvou neznámých:
1 + t = -1 - 2s,
2 - 2t = 6 + 4s.
Pokud první rovnici vynásobíme dvěma a přičteme ke druhé rovnici získáme
4 = 4. - To platí pro libovolnou hodnotu t a s a soustava tedy má nekonečně mnoho řešení, c ož znamená, že existuje nekonečně mnoho bodů ležících jak na přímce p, tak q, proto p = q.
Jak je vidět, mohli bychom použít výše zmíněné postupy pro zkoumání vzájemné polohy jakýchkoliv dvou přímek v rovině. Kontrola, zda jeden vektor je násobkem druhého je ale jednodušší, než řešit celou soustavu.
Vzájemnou polohu dvou přímek nemusíme určovat jen z parametrických rovnic. Můžeme využít i rovnice obecné nebo jejich kombinace.
Dvě přímky, které mají rovnice
ax + by + c = 0,
a'x + b'y + c' = 0,
- jsou rovnoběžné právě tehdy, je-li vektor n = (a; b) nenulovým reálným násobkem vektoru n' = (a'; b');
- jsou totožné právě tehdy, když je jedna rovnice násobkem druhé;
- jsou různoběžné právě tehdy, když má soustava jejich obecných rovnic právě jedno řešení.
Obecný tvar rovnice přímky neumožňuje zápis úsečky a polopřímky ležících na této přímce.
Určete vzájemnou polohu přímek p a q.
p: x + 2y - 1 = 0,
q: 3x + 6y = 2.
- Normálový vektor přímky p budeme značit jako np, analogicky normálový vektor přímky q jako nq.
np = (1; 2),
nq = (3; 6). - Ze zápisu je vidět, že nq je násobkem np, naše přímky jsou tedy rovnoběžné. Zbývá zjistit, zda jsou totožné nebo rovnoběžné různé.
- Pokud by rovnice q byla násobkem p, byly by totožné. Aby rovnice q byla násobkem rovnice p, musel by koeficient c v rovnici přímky q odpovídat hodnotě -3 (to plyne z toho, že vektor nq = 3np). Koeficient je roven jen -2, tedy p a q jsou rovnoběžné různé.
Určete vzájemnou polohu přímek p a q, je-li
p: x - y - 1 = 0,
q: 3x + 3y - 6 = 0. Jsou-li různoběžné, najděte i jejich průsečík.
- Najdeme normálové vektory přímek p a q:
np = (1; -1),
nq = (3; 3). - Vidíme, že vektor np není násobkem vektoru
nq, a proto přímky nejsou rovnoběžné a musí být tedy různoběžné (přímky p a q jsou na sebe dokonce kolmé
 ). Pokud přímky p a q nejsou rovnoběžné, má smysl hledat jejich společný bod. Ten získáme, pokud vyřešíme následující soustavu dvou rovnic o dvou neznámých:
). Pokud přímky p a q nejsou rovnoběžné, má smysl hledat jejich společný bod. Ten získáme, pokud vyřešíme následující soustavu dvou rovnic o dvou neznámých:
x - y = 1,
3x + 3y = 6. - Z první rovnice plyne x = y + 1. Po dosazení do druhé rovnice získáme:
3y + 3 + 3y = 6,
tedy x = 3/2 a y = 1/2. - Přímky p a q jsou různoběžné, jejich průsečíkem je bod \(X \left[\dfrac{1}{2}; \dfrac{3}{2}\right]\).
Určete vzájemnou polohu přímek p: x - 2y + 5 a q: x = 3 - 2t, y = 2 + t; t ∈ ![]() . Pokud existuje, najděte jejich průsečík.
. Pokud existuje, najděte jejich průsečík.
- Do obecné rovnice přímky p dosadíme za x a y vyjádřené souřadnice x a y z parametrické rovnice přímky q:
(3 - 2t) - 2(2 + t) + 5 = 0. - Tuto rovnici vyřešíme:
3 - 2t - 4 - 2t + 5 = 0,
-4t + 4 = 0,
t = 1. - Rovnice má jedno řešení. To znamená, že p × q a jejich průsečíkem je bod P[1; 3], který odpovídá hodnotě parametru t = 1 v parametrické rovnici přímky q.