\begin{align} \end{align}

Hyperbola

Poslední kuželosečkou, kterou si probereme je hyperbola. Hyperbola vznikne průnikem rotační kuželové plochy s rovinou, která neprochází jejím vrcholem a pro jejíž odchylku φ od osy rotace kuželové plochy platí: φ ∈ <0°; α), kde α je odchylka tvořících přímek kuželové plochy od její osy.

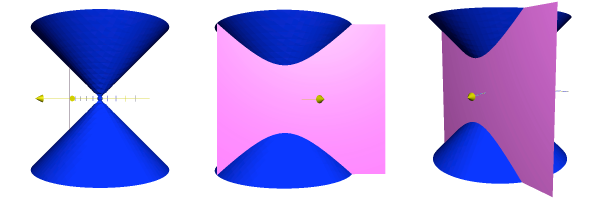
Obr 5.18: Hyperbola jako řez kuželové plochy rovinou
Obr 5.18: Hyperbola jako řez kuželové plochy rovinou
Definice

V rovině jsou dány dva různé body E, F. Množina všech bodů X této roviny, pro které se ||XE| - |XF|| rovná danému kladnému číslu, které je menší než |EF|, se nazývá hyperbola. Body E, F se nazývají ohniska hyperboly.

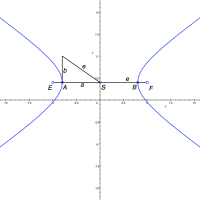
Obr. 5.20: Charakteristiky hyperboly
Obr. 5.20: Charakteristiky hyperboly

Střed S úsečky EF se nazývá střed hyperboly. Přímka EF hlavní osou a osa úsečky EF vedlejší osou hyperboly. Dvěma bodům A, B hyperboly, které leží na její hlavní ose, říkáme vrcholy hyperboly. Vzdálenost vrcholu hyperboly od středu nazýváme hlavní poloosa a hyperboly, vzdálenost ohniska od středu pak výstřednost (excentricita) e hyperboly. Hyperbola se skládá ze dvou větví. Jedna z nich je ta, která na obr. 5.20 obsahuje vrchol A, druhá potom vrchol B.

Přímky y = kx + c, které procházejí středem hyperboly a mají směrnici

\(|k| = \dfrac{b}{a}\)

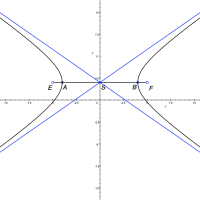
se nazývají asymptoty hyperboly. Jsou-li asymptoty navzájem kolmé, hyperbola se nazývá rovnoosá. Asymptoty hyperboly mají zajímavou vlastnost. Jejich vzdálenost od větví hyperboly se blíží k nule, ale nemají s ní žádný společný bod. Pokud bychom na obr. 5.21 obě větvě hyperboly a její asymptoty prodloužili donekonečna, viděli byste, že větve hyperboly se k asymptotám neustále přibližují, ale nikdy se jich nedotknou.

Obr. 5.21: Asymptoty hyperboly
Obr. 5.21: Asymptoty hyperboly
Definice

Rovnice
\(\dfrac{(x - m)^{2}}{a^{2}} - \dfrac{(y - n)^{2}}{b^{2}} = 1\), resp. \(-\dfrac{(x - m)^{2}}{a^{2}} + \dfrac{(y - n)^{2}}{b^{2}} = 1; a, b \ne 0\)
nazýváme středové rovnice hyperboly se středem S[m; n] a vrcholy A[m + a; n], B[m - a; n], resp. A[m; n + a], B[m; n - a] a výstředností \(e = \sqrt{a^{2} + b^{2}}\).

Hyperbola s rovnicí \(\dfrac{(x - m)^{2}}{a^{2}} - \dfrac{(y - n)^{2}}{b^2} = 1\) má hlavní osu rovnoběžnou s osou x.

Hyperbola s rovnicí \(-\dfrac{(x - m)^{2}}{a^{2}} + \dfrac{(y - n)^{2}}{b^2} = 1\) má hlavní osu rovnoběžnou s osou y.

Na obr. 5.22 je vlevo hyperbola s rovnicí \(\dfrac{x^{2}}{16} - \dfrac{y^{2}}{9} = 1\), vpravo potom hyperbola s rovnicí \(-\dfrac{x^{2}}{16} + \dfrac{y^{2}}{9} = 1\).

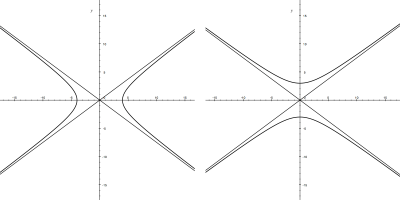
Obr. 5.22: Různé hyperboly
Obr. 5.22: Různé hyperboly
Poznámka

Asymptoty odpovídající rovnicím hyperboly v definici středové rovnice hyperboly jsou přímky

\(\dfrac{x - m}{a} = \pm \dfrac{y - n}{b}\)

Všimněte si, že asymptoty jsou jsou pro obě hyperboly stejné, jen poloha hyperboly se vzhledem k asymptotám liší.

Příklad 5.18

Určete středovou rovnici a asymptoty hyperboly se středem S[2; -1], ohniskem E[7; -1] a vrcholem A[5; -1].

Řešení
  • Ze souřadnic středu a vrcholu můžeme snadno spočítat hlavní poloosu a. Ze souřadnic středu a ohniska pak výstřednost e, zadané hyperboly. Platí:
    a = |SA| = 3,
    e = |SE| = 5.
  • Z hodnot a a e můžeme dopočítat koeficient b, který potřebujeme znát, abychom mohli vyjádřit středovou rovnici hyperboly: \(b = \sqrt{e^{2} - a^{2}}\).
  • Zbývá zvolit správný tvar její středové rovnice. Ze souřadnic bodů S a E vyčteme, že hlavní osa hyperboly je rovnoběžná s osou xnapoveda. Zadaná hyperbola má rovnici: \(\dfrac{(x - 2)^{2}}{9} - \dfrac{(y + 1)^{2}}{16} = 1\).
  • Rovnice \(\dfrac{x - 2}{3} = \pm \dfrac{y + 1}{4}\) odpovídají asymptotám zadané hyperboly. Upravíme-li je, získáme:
    4x - 3y - 11 = 0,
    4x + 3y - 5 = 0.
Definice

Rovnice hyperboly ve tvaru px2 + qy2 + 2rx + 2sy + t = 0; p, q, r, s ∈ realne cislo, p⋅q < 0, se nazývá obecná rovnice hyperboly.

Poznámka

Ne každá rovnice v tomto tvaru je rovnicí hyperboly.

Příklad 5.19

Najděte střed, ohniska, hlavní vrcholy a asymptoty hyperboly, dané rovnicí: 9x2 - 90x - 16y2 - 96y + 225 = 0.

Řešení
  • Upravíme obecnou rovnici na středovou, ze které dokážeme celou řadu údajů přímo vyčíst.
    9(x2 - 10x) - 16(y2 + 6y) + 225 = 0,
    9(x2 - 10x + 25) - 9⋅25 - 16(y2 + 6y + 9) + 16⋅9 + 225 = 0,
    9(x - 5)2 - 16(y + 3)2 = -144,
    \(-\dfrac{(x - 5)^{2}}{16} + \dfrac{(y + 3)^{2}}{9} = 1\).
  • Z této rovnice určíme souřadnice středu hyperboly, její hlavní a vedlejší poloosu. Střed S má souřadnice S[5; -3], hlavní poloosa a = 4, vedlejší poloosa b = 3. Z a a b dopočítáme výstřednost \(e = \sqrt{16 + 9} = 5\). Tvar středové rovnice odpovídá hyperbole, jejíž hlavní osa je rovnoběžná s osou y. To nám stačí k určení souřadnic ohnisek E, F a hlavních vrcholů A, B; E[5; 2], F[5; -8], A[5; 0] a B[5; -6].
  • Rovnice asymptot získáme úpravou rovnic \(\dfrac{x - 5}{4} = \pm \dfrac{y + 3}{3}\). Ty upravíme na:
    a1: 3x - 4y - 27 = 0,
    a1: 3x + 4y - 3 = 0.
Úloha

Napište obecnou rovnici hyperboly s asymptotami a1: 3x + 2y - 9 = 0, a2: 3x - 2y - 9 = 0 a vrcholem A[3; 3].

Řešení