Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Pythagorova věta
Pravoúhlý trojúhelník
Pravoúhlý trojúhelník
je trojúhelník, jehož jeden vnitřní úhel je pravý. Zbývající úhly musí být ostré,
protože součet velikostí vnitřních úhlů v každém trojúhelníku je 180°.
Přeponou nazýváme stranu ležící proti pravému úhlu,
odvěsnami pak strany ležící proti zbývajícím úhlům.
Pythagorova věta
V každém pravoúhlém trojúhelníku platí 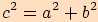 ,
kde
,
kde 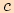 je délka přepony,
je délka přepony,
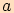 ,
, 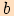 jsou délky jeho odvěsen.
jsou délky jeho odvěsen.
Pythagorova věta
Jiná formulace věty. Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců nad jeho odvěsnami.
Věta obrácená.
Jsou-li 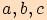 délky stran v trojúhelníku
a platí-li pro ně
délky stran v trojúhelníku
a platí-li pro ně 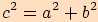 ,
pak je trojúhelník pravoúhlý a
,
pak je trojúhelník pravoúhlý a 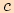 je délka přepony.
je délka přepony.
Důkaz

Představme si libovolný pravoúhlý trojúhelník 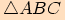 s délkou
přepony
s délkou
přepony 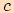 a odvěsnami
a odvěsnami 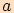 ,
,
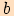 .
Sestrojíme nyní dva shodné čtverce o straně
.
Sestrojíme nyní dva shodné čtverce o straně 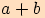 a do každého z nich umístíme čtyři shodné
a do každého z nich umístíme čtyři shodné  .
Obsahy vybarvených částí musí být stejné. V levém obrázku jsou vybarveny dva čtverce,
které mají obsahy
.
Obsahy vybarvených částí musí být stejné. V levém obrázku jsou vybarveny dva čtverce,
které mají obsahy 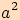 a
a 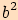 .
V pravém obrázku má vybarvený čtyřúhelník délky všech stran
.
V pravém obrázku má vybarvený čtyřúhelník délky všech stran 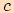 a protože
a protože 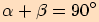 , má čtyřúhelník všechny
vnitřní úhly pravé, je to tedy čtverec a jeho obsah je
, má čtyřúhelník všechny
vnitřní úhly pravé, je to tedy čtverec a jeho obsah je 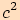 .
Vybarvené části mají stejný obsah a proto platí
.
Vybarvené části mají stejný obsah a proto platí 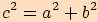 .
.
Příklady
 , jsou-li dány délky
stran
, jsou-li dány délky
stran 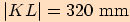 ,
, 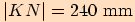 .
.
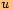 ,
rozdělí obdélník
,
rozdělí obdélník na dva shodné pravoúhlé trojúhelníky.
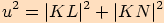

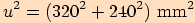

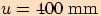

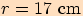 a délka základny
a délka základny 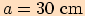 .
.
 .
. Pomocí Pythagorovy věty vypočítáme výšku
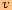 .
. 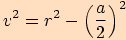

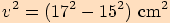

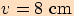

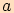 .
. stěnová úhlopříčka:
stěnová úhlopříčka:

 .
.Vypočítáme úhlopříčku, kterou označíme
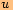 .
. 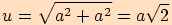
 tělesová úhlopříčka:
tělesová úhlopříčka:

 ,
,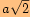 , kde tělesová úhlopříčka je přeponou,
označíme ji
, kde tělesová úhlopříčka je přeponou,
označíme ji 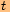 .
.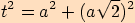

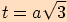
Stěnová úhlopříčka má délku
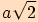 ,
tělesová úhlopříčka
,
tělesová úhlopříčka 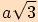 .
.

>>>nahoru<<