Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Goniometrické funkce ostrého úhlu
Definice. Je dán pravoúhlý trojúhelník s jedním vnitřním
úhlem 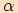 , jehož velikost je z intervalu
, jehož velikost je z intervalu 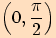 .
Definujme tyto goniometrické funkce:
.
Definujme tyto goniometrické funkce:
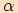
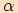
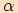
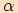
Poznámka.
Většinou užíváme následujícího značení 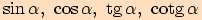 .
.
Pro schematický zápis použijeme trojúhleník 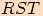 .
.
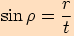
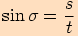
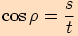
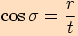
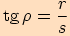
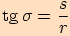
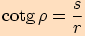
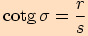
Odvození funkčních hodnot
Funkční hodnoty goniometrických funkcí pro různé velikosti úhlu 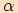 najdeme v tabulkách nebo je vypočítáme pomocí kalkulačky, případně k jejich určení
použijeme applet, který najdeme níže v této kapitole.
najdeme v tabulkách nebo je vypočítáme pomocí kalkulačky, případně k jejich určení
použijeme applet, který najdeme níže v této kapitole.
Předtím si ještě odvodíme funkční hodnoty pro úhly o velikostech 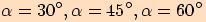 ,
pro něž lze tyto hodnoty přesně určit.
,
pro něž lze tyto hodnoty přesně určit.
A.
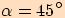
Je dán čtverec se stranou
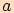 , pomocí Pythagorovy věty vypočítáme délku jeho úhlopříčky
, pomocí Pythagorovy věty vypočítáme délku jeho úhlopříčky
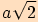 .
Z vlastností čtverce víme, že úhlopříčka a strana svírají úhel o velikosti
.
Z vlastností čtverce víme, že úhlopříčka a strana svírají úhel o velikosti 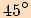 .
Vyjádříme funkční hodnoty pro tento úhel
.
Vyjádříme funkční hodnoty pro tento úhel 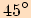 :
:
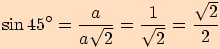
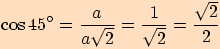
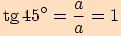
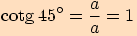
B.
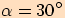
Je dán rovnostranný trojúhelník se stranou délky 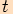 .
Dle Pythagorovy věty vypočítáme výšku
.
Dle Pythagorovy věty vypočítáme výšku 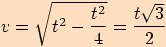 .
.
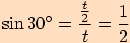
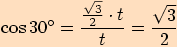
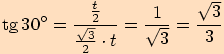
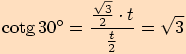
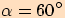
Využijeme stejného rovnostranného trojúhelníku se stranou délky
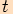 .
.
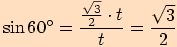
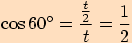
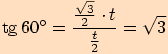
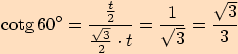
Tabulka
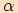 | 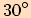 |
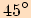 | 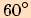 |
|---|---|---|---|
sinus 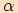 |
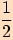 |
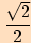 |
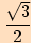 |
kosinus 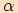 |
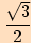 |
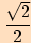 |
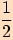 |
tangens 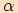 |
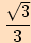 |
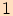 |
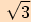 |
kotangens 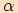 |
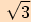 |
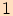 |
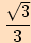 |
Výpočet velikosí úhlů a určení funkčních honot u goniometrických funkcí
>>nahoru<<Poznámka. Tabulka s některými dalšími funkčními hodnotami je uvedena v kapitole Určování hodnot goniometrických funkcí. Na tomto místě nelze například odvodit funkční hodnoty pro nulový úhel, protože neexistuje trojúhelník, který by měl jeden úhel nulový.
Z předchozích výpočtů jsme si mohli všimnout následujících vztahů:
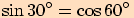
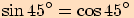
 Stačí si uvědomit, že v pravoúhlém trojúhelníku
Stačí si uvědomit, že v pravoúhlém trojúhelníku
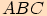 platí:
platí:
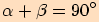

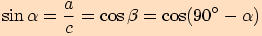

Pravoúhlý trojúhelník
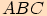
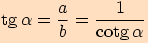
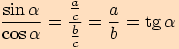
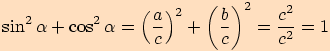
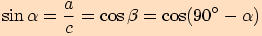
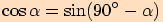

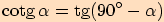
Příklady
1.
Pomocí kalkulačky vypočítejte s přesností na dvě desetinná místa sinus těchto úhlů 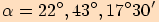 .
.

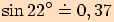

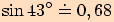

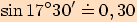

2.
Pro jaký úhel je jeho sinus roven 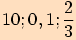 ?
?

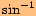 .
.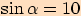 , neexistuje úhel, který by vyhovoval.
Neboť funkce sinus je dána podílem dvou stran. V čitateli je délka odvěsny a ve
jmenovateli je délka přepony. Délka přepony nemůže být delší než délka odvěsny,
tudíž podíl (a tedy i sinus tohoto úhlu) je vždy menší než
, neexistuje úhel, který by vyhovoval.
Neboť funkce sinus je dána podílem dvou stran. V čitateli je délka odvěsny a ve
jmenovateli je délka přepony. Délka přepony nemůže být delší než délka odvěsny,
tudíž podíl (a tedy i sinus tohoto úhlu) je vždy menší než 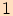 .
.
 Pro
Pro 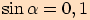 je
je 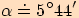 .
. Pro
Pro 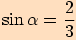 je
je 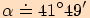 .
.
3.
Pomocí kalkulačky vypočítejte s přesností na dvě desetinná místa kosinus těchto úhlů 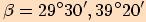 .
.

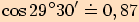

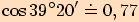

4.
Pro jaký úhel je jeho kosinus roven 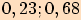 ?
?

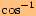 .
.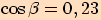 je
je 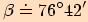 .
. Pro
Pro 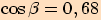 je
je 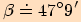 .
.

5.
Pomocí kalkulačky vypočítejte s přesností na dvě desetinná místa tangens těchto úhlů 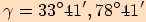 .
.

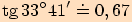

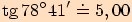

6.
Pro jaký úhel je jeho tangens roven 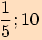 ?
?

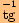 .
.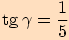 je
je 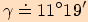 .
. Pro
Pro 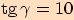 je
je 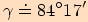 .
.

7.
Pomocí kalkulačky vypočítejte s přesností na dvě desetinná místa kotangens těchto úhlů
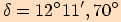 .
.

tudíž použijeme vztah mezi funkcemi tangens a kotangens
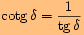 .
.
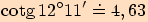

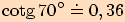

8.
Pro jaký úhel je jeho kotangens roven 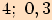 ?
?

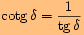 .
.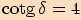

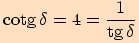

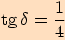

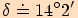
 b)
b) 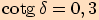

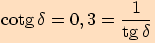

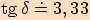

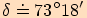

9.
Vypočtěte velikost úhlu 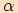 , který svírají tečny
, který svírají tečny
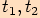 vedené bodem
vedené bodem 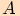 ke kružnici
ke kružnici  , je-li
, je-li 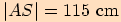 .
.

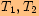 body dotyku a
body dotyku a
 poloměr kružnice.
poloměr kružnice. Máme zde shodné trojúhelníky
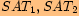 .
. Vypočítáme velikosti úhlu
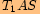 .
.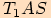 je
je 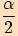 .
.
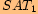
vyjádříme úhel
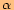 .
.
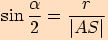

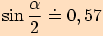

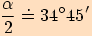



10.
Dělostřelecká baterie je umístěna na útesu vysokém 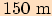 nad hladinou moře. Určete vzdálenost
nad hladinou moře. Určete vzdálenost 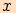 baterie od lodi, která je
z útesu pozorována v hloubkovém úhlu
baterie od lodi, která je
z útesu pozorována v hloubkovém úhlu 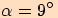 .
.

oka pozorovatele a bodu na pozorovaném objektu.
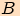 , loď
, loď 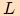 a patu
útesu
a patu
útesu 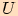 . Hledaná vzdálenost je
. Hledaná vzdálenost je
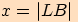 .
.
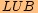 je pravoúhlý s pravým úhlem u vrcholu
je pravoúhlý s pravým úhlem u vrcholu 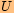 .
.U vrcholu
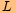 je také úhel
je také úhel  ,
jde o střídavé úhly.
,
jde o střídavé úhly.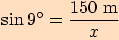

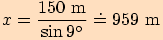

11.
V kosočtverci 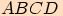 je
je 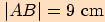 a velikost úhlu
a velikost úhlu 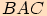 je
je 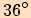 .
Vypočítejte poloměr kružnice, která je tomuto kosočtverci vepsána.
.
Vypočítejte poloměr kružnice, která je tomuto kosočtverci vepsána.

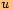 ,
,protože úhlopříčky v kosočtverci jsou na sebe kolmé.
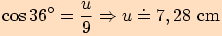

je polovina úhlopříčky a odvěsna hledaný poloměr.
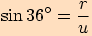

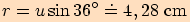

12. Mostní kruhový oblouk má rozpětí
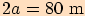 a výšku
a výšku
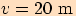 .
Vypočtěte velikost příslušného středového úhlu
.
Vypočtěte velikost příslušného středového úhlu 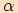 .
.

 Označíme bod
Označíme bod 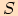 jako střed kružnice, jejíž částí je daný mostní oblouk,
jako střed kružnice, jejíž částí je daný mostní oblouk, 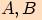 jako body,
ve kterých se most dotýká hladiny a bod
jako body,
ve kterých se most dotýká hladiny a bod 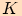 jako střed úsečky
jako střed úsečky 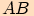 .
.
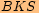 vypočítáme nejprve
vypočítáme nejprveužitím Pythagorovy věty poloměr kruhového oblouku
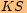 .
.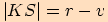

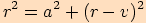

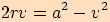

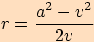



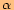 .
.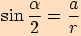

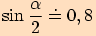

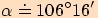

>>nahoru<<