Věta o polovičních úhlech Další trigonometrické věty Úlohy k opakování 1 Velikost úhlu Orientovaný úhel Funkce sinus a kosinus Funkce tangens a kotangens Určování hodnot goniometrických funkcí Grafy goniometrických funkcí Vzorce pro goniometrické funkce Úlohy k opakování 2 Odkazy Literatura
Harmonické funkce, jejich grafy a grafy dalších goniometrických funkcí
Definice. Harmonickou funkcí
nazýváme funkci typu 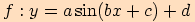 , kde
, kde
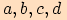 jsou reálné konstanty,
jsou reálné konstanty,
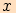 je reálná proměnná,
je reálná proměnná, 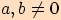 .
.
Poznámka. Tyto funkce se hojně používají ve fyzice a v technice.
Graf harmonické funkce sestrojíme s využitím znalosti grafu funkce 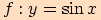 .
Ta je vlastně speciálním případem harmonické funkce, kde
.
Ta je vlastně speciálním případem harmonické funkce, kde 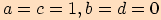 .
.
Postup při tvorbě grafů těchto funkcí si ukážeme na příkladech.
1) 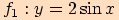
Graf funkce 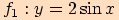 získáme zdvojnásobením všech
získáme zdvojnásobením všech 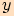 -ových
souřadnic bodů grafu funkce
-ových
souřadnic bodů grafu funkce 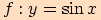 .
.
2) 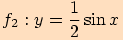
Graf funkce 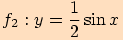 dostaneme, jestliže všechny
dostaneme, jestliže všechny
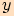 -ové
souřadnice bodů grafu funkce
-ové
souřadnice bodů grafu funkce 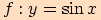 zmenšíme na polovinu.
zmenšíme na polovinu.
3) 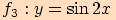
Složená funkce 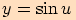 , kde
, kde 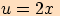 ,
má základní periodu
,
má základní periodu 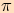 , protože je
, protože je
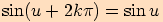 čili
čili 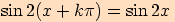 pro každé
pro každé 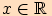 ,
, 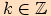 .
Graf této funkce vznikne "smrštěním" grafu funkce
.
Graf této funkce vznikne "smrštěním" grafu funkce 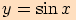 ve směru osy
ve směru osy 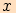 .
.
4) 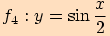
Podobně tato složená funkce 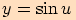 , kde
, kde 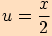 ,
má základní periodu
,
má základní periodu 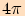 ,
protože platí
,
protože platí 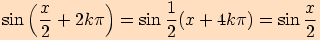 pro každé
pro každé
 ,
,  .
Graf této funkce vznikne "roztažením" grafu funkce
.
Graf této funkce vznikne "roztažením" grafu funkce 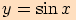 ve směru osy
ve směru osy 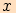 .
.
5) 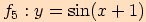
Složená funkce, která je dána předpisem 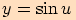 ,
kde
,
kde 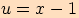 , má základní periodu
, má základní periodu 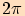 ,
jako funkce
,
jako funkce 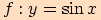 , neboť platí
, neboť platí 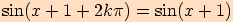 pro každé
pro každé 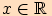 ,
, 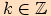 .
.
Graf funkce dostaneme z grafu 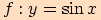 posunutím
o 1 jednotku ve směru záporné poloosy
posunutím
o 1 jednotku ve směru záporné poloosy 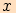 (tj. doleva).
(tj. doleva).
6) 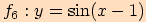
Složená funkce dána předpisem 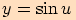 , kde
, kde
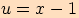 ,
má základní periodu
,
má základní periodu 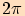 , jako funkce
, jako funkce
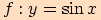 ,
neboť platí
,
neboť platí 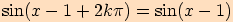 pro každé
pro každé 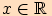 ,
,
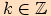 .
.
Graf funkce 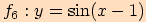 dostaneme z grafu
dostaneme z grafu 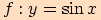 posunutím
o 1 jednotku ve směru kladné poloosy
posunutím
o 1 jednotku ve směru kladné poloosy 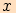 (tj. doprava).
(tj. doprava).
7) 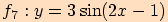
Jde o složenou funkci s předpisem 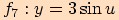 , kde
, kde 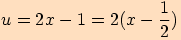 ,
pro každé
,
pro každé 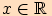 ,
,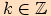 .
.
Graf funkce 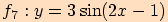 dostaneme postupně z grafů
dostaneme postupně z grafů
a) 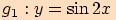 (viz příklad 3)
(viz příklad 3)
b) 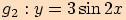 (viz příklad 1) ztrojnásobením funkčních hodnot funkce
(viz příklad 1) ztrojnásobením funkčních hodnot funkce
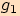
c) 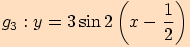 (viz příklad 5) posunutím funkce
(viz příklad 5) posunutím funkce
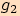 o
o 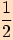 ve směru kladné poloosy
ve směru kladné poloosy 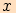 (tj. doprava).
(tj. doprava).
8) 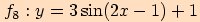
Graf této funkce získáme posunutím funkce 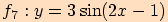 o
o
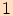 jednotku
ve směru kladné poloosy
jednotku
ve směru kladné poloosy 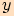 (tj. nahoru).
(tj. nahoru).
Harmonická funkce (graf funkce sinus s nastavitelnými parametry)
Graf funkce kosinus s nastavitelnými parametry
Graf funkce tangens s nastavitelnými parametry
Graf funkce kotangens s nastavitelnými parametry
Příklady
V příkladech jsou uvedeny pouze nápovědy, jak sestrojit graf. Ke kontrole toho, jak grafy vypadají, použijte applety.
Načrtněte grafy těchto funkcí :
a) 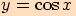


b) 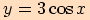

 -ové souřadnice
-ové souřadnicefunkce
 .
.

c) 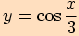

 , kde
, kde
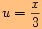 ,
,která má nejmenší periodu
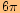
neboť
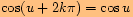
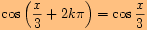
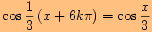

d) 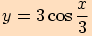

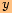 -ové souřadnice funkce
-ové souřadnice funkce 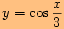

e) 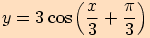

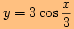 o
o 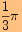
doleva ve směru osy
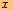 .
.
f) 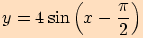

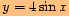 posunutý o
posunutý o 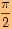
doprava ve směru osy
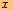 .
. 
g) 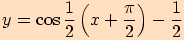

 posunutý o
posunutý o 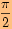
doleva ve směru osy
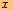 a
ao
 jednotky dolů ve směru osy
jednotky dolů ve směru osy 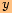 .
.

h) 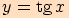

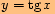 .
.

i) 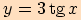

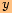 -ové souřadnice
-ové souřadnicefunkce
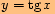 .
.
j) 

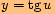 ,
,kde
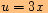 ,
, která má nejmenší periodu
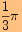
neboť
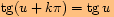
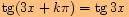
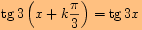

k) 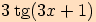

 ,
která je posunutá o
,
která je posunutá o 
doleva ve směru osy
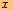 .
.
l) 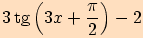

 ,
posunutou o
,
posunutou o 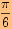 doleva ve
směru osy
doleva ve
směru osy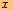 a
ao
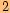 jednotky dolů ve směru osy
jednotky dolů ve směru osy 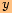 .
.
m) 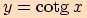

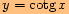 .
.

n) 

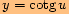 ,
,
kde
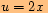 ,
která má nejmenší periodu
,
která má nejmenší periodu 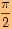
neboť
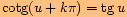
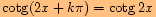
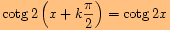

o) 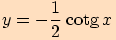

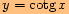 vynásobíme
vynásobíme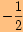

p) 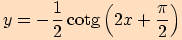

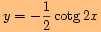 ,
posunutou o
,
posunutou o 
doleva ve směru osy
 .
. 
q) 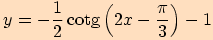

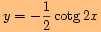 ,
posunutou o
,
posunutou o 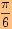
doprava ve směru osy
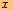 a
a o
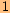 jednotku dolů ve směru osy
jednotku dolů ve směru osy 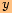 .
.
r) 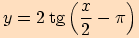

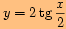 ,
,posunutou o
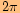
doprava ve směru osy
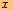 .
.

s) 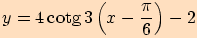

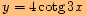 ,
posunutou o
,
posunutou o 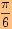
doprava ve směru osy
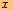
a o
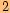 jednotky dolů ve směru osy
jednotky dolů ve směru osy 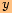 .
.
>>nahoru<<