Algebraická geometrie [Jan Šťovíček]

Základní informace

Sylabus a základní informace viz popis předmětu ve Studijním informačním systému.

Rozvrh (k nalezení též v SISu):

přednáška v pondělí 9:00-10:30 v místnosti K9,
cvičení (cvičí L. Shaul) ve středu 9:00-10:30 v místnosti K7.

Zkouška

Zkouška je ústní a termíny jsou podle individuální domluvy.

Zápočet

Zápočet bude udělován za odevzdané vyřešené úkoly. Půjde o tři sady problémů, které budou vypisovány níže. Požaduji alespoň 50 % bodů z vyřešených problémů v uvedených termínech.

Příklady č. 1 (termín odevzdání 19. listopadu)

Komplexní algebraickou podmnožinu X ⊆ A² nazveme kuželosečkou, pokud je tvaru X = V(f), kde f ∈ C[x,y] je nenulový polynom celkového stupně 2. Ukažte, že každá ireducibilní kuželosečka je isomorfní buď V(y-x²) nebo V(xy-1).
Nechť C je těleso komplexních čísel a uvažujte okruh R = C[x,y,z]/(xz,yz) a prvek f := y-z ∈ R. Ukažtě, že lokalizovaný okruh R_f (kde invertujeme prvek f ∈ R) je isomorfní okruhu C[x,y^±1] × C[z^±1].
Najděte biracionální ekvivalenci mezi komplexní afinní přímkou a komplexní rovinnou křivkou V(y³+x²-yx²) ⊆ A². Najděte řešení rovnice y³+x²-yx² = 0 nad racionálními čísly.

Příklady č. 2 (termín odevzdání 17. prosince)

Ukažte, že obraz polynomiálního zobrazení f: A¹ → A³ daného předpisem f(t) = (t³, t⁴, t⁵) nad tělesem komplexních čísel je podvarieta A³. Ukažte navíc, že je to přesně množina nul polynomu y² - xz a determinantu matice

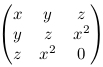
$\begin{pmatrix} x & y & z \\ y & z & x^2 \\ z & x^2 & 0 \end{pmatrix}$

(nápověda: je-li x nenulové, můžeme položit t=y/x a vydělit řádky matice prvkem x).

Ukažte nakonec, že polynom p = x³ - yz se na obrazu f nuluje a najděte vyjádření nějaké mocniny p^e jakožto prvku ideálu C[x,y,z] generovaného polynomem y² - xz a determinantem (takové vyjádření musí z Hilbertovy věty o nulách existovat).
Nechť K je algebraicky uzavřené těleso. Definujeme zobrazení i z množiny dvoudimenzionálních vektorových podprostorů V ⊆ K⁴ do projektivního prostoru P⁵ následovně. Vezmeme ve V libovolné dva lineárně nezávislé vektory v = (a₀, a₁, a₂, a₃) a w = (b₀, b₁, b₂, b₃), jejich složky zapíšeme do matice 2x4

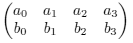
$\begin{pmatrix} a_0 & a_1 & a_2 & a_3 \\ b_0 & b_1 & b_2 & b_3 \end{pmatrix}$

a spočítáme (v nějakém pevném pořadí) všech 6 determinantů d₀, d₁, ..., d₅ podmatic velikosti 2x2. Pak i bude zobrazovat V na (d₀ : d₁ : ... : d₅).
1. Ukažte, že i je dobře definované prosté zobrazení.
2. Ukažte, že obraz X zobrazení i je projektivní varieta zadaná v P⁵ jednou kvadratickou rovnicí.

Příklady č. 3 (termín odevzdání: u zkoušky)

Uvažujte nad komplexními čísly podmnožinu B ⊆ A³ × P² tvořenou všemi body (x,y,z, (s:t:u)) takovými, že (s,t,u) a (x,y,z) jsou lineárně závislé vektory.
1. Ukažte, že B je podvarieta A³ × P².
2. Ukažte, že při projekci π: B → A³ dané předpisem π(x,y,z, (s:t:u)) = (x,y,z) má počátek souřadnic 0 ∈ A³ vzor isomorfní P² a že π se zúží na isomorfismus kvaziprojektivních variet B\π^-1(0) → A³\{0} (tj. B je blow up počátku souřadnic v A³).
3. Buď X=V(x²-y²-z²) ⊆ A³. Najděte v B Zariského uzávěr Y množiny π^-1(X\{0}) a ukažte, že π se zúží na isomorfismus Y\π^-1(0) → X\{0}.
4. Nakonec ukažte, Y má otevřené pokrytí otevřenými množinami isomorfními A² (čili jsme se zbavili singularity X v počátku souřadnic).
Uvažujte desetidimenzionální komplexní vektorový prostor V tvořený všemi polynomy z C[x,y] stupně nejvýše 3 a odpovídající projektivní prostor P⁹ tvořený přímkami ve V. Ukažte, že ireducibilní kubické křivky v komplexním afinním prostoru A² jsou parametrizovány Zariski otevřenou podmnožinou P⁹ (tedy ireducibilní kubické křivky samy tvoří kvaziprojektivní varietu).
Spočítejte (a zdůvodněte!), jaká je Krullova dimenze Grassmannovy variety X z druhého příkladu druhé série.

Co bylo probráno

Zde je uveden orientační seznam probrané látky po jednotlivých přednáškách, včetně odkazů do literatury.

1. 10. 2018: Afinní algebraické množiny, Zariského topologie, rozklad noetherovského topologického prostoru na ireducibilní komponenty, plus na cvičení ideál podmnožiny afinního prostoru a algebraické podmnožiny afinní roviny (skripta, kap. 1; [Ful], kap. 1.2 - 1.6, 6.1; [Ga], kap. 1.1, 1.3).
8. 10. 2018: Důkaz k rozkladu noetherovského topologického prostoru na ireducibilní komponenty, charakterizace ireducibility přes prvoideály, polynomiální zobrazení a souřadnicové okruhy, bijekce mezi polynomiálními zobrazeními a homomorfismy souřadnicových okruhů (skripta, kap. 1 a 2; [Ful], kap. 1.5, 2.1 - 2.2; [Ga], kap. 1.3, 2.1).
15. 10. 2018: Důkaz k bijekci mezi polynomiálními zobrazeními a homomorfismy souřadnicových okruhů, polynomiální isomorfismy a změny souřadnic, funkční tělesa a racionální funkce na varietách, regulární body a póly, příklady (skripta, kap. 2; [Ful], kap. 2.2 - 2.4; [Ga], kap. 2.1, 2.3, [Sh], kap. 3).
22. 10. 2018: Racionální zobrazení mezi varietami, vztah mezi racionálními zobrazeními s hustým obrazem a homomorfismy funkčních těles (skripta, kap. 2; [Ful], kap. 6.6; [Ga], kap. 2.1, 2.3; [Sh], kap. 3).
29. 10. 2018: Biracionální ekvivalence, racionální variety, lokalizace okruhů (skripta, kap. 2 a 3; [Ful], kap. 6.6; [Ga], kap. 2.1, 2.3, 4.3; [Sh], kap. 3; [AM], kap. 3).
5. 11. 2018: Lokalizace v multiplikativní množině, geometrický význam lokalizace K[X] → K[X]_f, radikálové ideály, Hilbertova věta o nulách (skripta, kap. 3; [Ful], kap. 1.7 - 1.10, 6.3; [Ga], kap. 1.2, 2.1; [AM], kap. 3).
12. 11. 2018: Důsledky věty o nulách, rekonstrukce algebraické množiny ze souřadnicového okruhu, otevřená báze Zariského topologie, lokální okruhy, na cvičení disktrétní valuační obory (skripta, kap. 3 a 4; [Ful], kap. 1.7, 2.4, 2.5, 6.3; [Ga], kap. 1.2, 2.1).
19. 11. 2018: Lokální okruhy v bodech algebraické množiny a jejich vlastnosti, rovinné křivky, singulární a nesingulární body na nich, tečny (skripta, kap. 4; [Ful], kap. 2.4, 3.1; [Ga], kap. 2.1, 4.4; text o rovinných křivkách).
26. 11. 2018: Diskrétní valuační obory a charakterizace nesingulárních bodů na rovinných křivkách, ([Ful], kap. 2.5, 3.2; [Ga], kap. 4.4).
3. 12. 2018: Projektivní algebraické množiny, projektivní Zariského topologie, homogenní ideály a homogenní souřadnicové okruhy, rozklad na ireducibilní komponenty, projektivní věta o nulách ([Ful], kap. 2.6, 4.1, 4.2; [Ga], kap. 3.1, 3.2).
10. 12. 2018: Kvaziprojektivní algebraické množiny a svazek regulárních funkcí na nich, homomorfismy a kartézské součiny kvaziprojektivních algebraických množin ([Ful], kap. 4.3, 6.2 - 6.4; [Ga], kap. 3.3; [Sh], kap. 5.1).
17. 12. 2018: Separovanost kvaziprojektivních algebraických množin coby náhrada za nehausdorffovskost Zariského topologie, projektivní eliminace, uzavřenost obrazu pro homomorfismy z projektivních algebraických množin, verze stereografické projekce v projektivní geometrii, na cvičení nafouknutí (blow up) bodu a řešení singularit ([Ful], kap. 4.4, 6.4, 7.2; [Ga], kap. 3.3, 3.4, 4.3; [Sh], kap. 5.2).
7. 1. 2019: Krullova dimenze a její výpočet pro afinní a projektivní prostory ([Ful], kap. 6.5; [Ga], kap. 1.4, 4.1 - 4.2; [Sh], kap. 5.3 - 5.4, 6.1).

Literatura

K přednášce budu v tomto semestru průběžně aktualizovat předběžnou verzi skript: [PDF ke stažení]

Co se další literatury týče, algebraická geometrie postupně vyrostla ve velmi široký obor, o kterém jsou napsány tisíce stránek z různých pohledů. Určitou představu (příp. doporučení, kudy dále pro zájemce) si lze udělat na tomto blogu na mathoverflow.net. Přednáška je inspirována následujícími dvěma zdroji, které jsou volně dostupné on-line v PDF, a proto do nich u seznamu probrané literatury uvádím odkazy:

[Ga]	A. Gathmann, Algebraic geometry, skripta kurzu z Kaiserslautern, 2002/2003. [PDF ke stažení]
[Ful]	W. Fulton, Algebraic Curves (An Introduction to Algebraic Geometry), 2008. [PDF ke stažení]

Další inspirace a fakta pochází především z těchto (off-line) zdrojů:

[AM]	M. F. Atiyah, I. G. MacDonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Co., 1969.
[CLO]	D. Cox, J. Little, D. O'Shea, Ideals, varieties, and algorithms, Second Edition, Springer, New York, 2005.
[Na]	M. Nagata, Local Rings, John Wiley & Sons, 1962.
[Nee]	A. Neeman, Algebraic and Analytic Geometry, LMS Lecture Note Series 345, Cambridge, 2007.
[Sh]	I. R. Shafarevich, Basic algebraic geometry 1, Varieties in projective space, 2. vyd., Springer-Verlag, Berlin, 1994.

V češtině lze leccos nalézt i v provizorních skriptech od prof. Drápala:

[Dr1]	A. Drápal, Komutativní okruhy. [PDF ke stažení]
[Dr2]	A. Drápal, Algebraická geometrie - geometrická čast. [PDF ke stažení]
[Dr3]	A. Drápal, Algebraická geometrie - algebraická čast. [PDF ke stažení]

Algebraická geometrie