Upozornění: Tato stránka se týkala přednášky v zimním semestru 2017/2018. Odkaz na aktuální přednášku hledejte na domovské stránce.
Základní informace
Sylabus a základní informace viz popis předmětu ve Studijním informačním systému.
Rozvrh (k nalezení též v SISu):
- přednáška v pátek 12:20-13:50 hod. v místnosti K9,
- cvičení v pátek 14:00-15:30 hod. v místnosti K9.
Zkouška
Zkouška je ústní a termíny jsou podle individuální domluvy.
Zápočet
Zápočet bude udělován za odevzdané vyřešené úkoly. Půjde o tři sady problémů, které budou vypisovány níže. Požaduji alespoň 50 % bodů z vyřešených problémů v uvedených termínech.
Příklady č. 1 (termín odevzdání 24. listopadu)
- Komplexní algebraickou podmnožinu X ⊆ A2 nazveme kuželosečkou, pokud je tvaru X = V(f), kde f ∈ C[x,y] je nenulový polynom celkového stupně 2. Ukažte, že každá ireducibilní kuželosečka je isomorfní buď V(y-x2) nebo V(xy-1).
- Nechť C je těleso komplexních čísel a uvažujte okruh R = C[x,y,z]/(xz,yz) a prvek f := y-z ∈ R. Ukažtě, že lokalizovaný okruh Rf (kde invertujeme prvek f ∈ R) je isomorfní okruhu C[x,y±1] × C[z±1].
- Uvažujte podalgebru R ⊆ C[x,y] tvořenou polynomy se členy pouze sudého celkového stupně. Najděte algebraickou množinu X takovou, že R je isomorfní souřadnicovému okruhu C[X].
Příklady č. 2 (termín odevzdání 22. prosince)
-
Ukažte, že obraz polynomiálního zobrazení f: A1 → A3 daného předpisem f(t) = (t3, t4, t5) nad tělesem komplexních čísel je podvarieta A3. Ukažte navíc, že je to přesně množina nul polynomu y2 - xz a determinantu matice
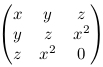
(nápověda: je-li x nenulové, můžeme položit t=y/x a vydělit řádky matice prvkem x).
Ukažte nakonec, že polynom p = x3 - yz se na obrazu f nuluje a najděte vyjádření nějaké mocniny pe jakožto prvku ideálu C[x,y,z] generovaného polynomem y2 - xz a determinantem (takové vyjádření musí z Hilbertovy věty o nulách existovat).
- Uvažujte kubickou rovinnou křivku X = V(x3 + y3 - 3x2 - 3y2 +3xy +1) nad tělesem komplexních čísel. Najděte všechny singulární body X. Dále najděte konkrétní biracionální ekvivalenci f: A1 → X (nápověda: stereografická projekce se středem v singulárním bodě X).
- Nechť K je algebraicky uzavřené těleso a I ⊆ K[x1, ..., xn] je ideál. Ukažte, že radikál ideálu I je roven průniku všech maximálních ideálů K[x1, ..., xn], které I obsahují.
Příklady č. 3 (termín odevzdání 12. ledna)
-
Nechť K je algebraicky uzavřené těleso. Definujeme zobrazení i z množiny dvoudimenzionálních vektorových podprostorů V ⊆ K4 do projektivního prostoru P5 následovně. Vezmeme ve V libovolné dva lineárně nezávislé vektory v = (a0, a1, a2, a3) a w = (b0, b1, b2, b3), jejich složky zapíšeme do matice 2x4
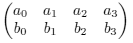
a spočítáme (v nějakém pevném pořadí) všech 6 determinantů d0, d1, ..., d5 podmatic velikosti 2x2. Pak i bude zobrazovat V na (d0 : d1 : ... : d5).
- Ukažte, že i je dobře definované prosté zobrazení.
- Ukažte, že obraz X zobrazení i je projektivní varieta zadaná v P5 jednou kvadratickou rovnicí.
-
Uvažujte zobrazení f: P1 → P3 nad tělesem komplexních čísel dané předpisem f((s:t)) = (s3:s2t:st2:t3).
- Ukažte, že f je dobře definovaný homomorfismus projektivních algebraických množin.
- Najděte konkrétní homogenní polynomy f1, f2, ..., fr ∈ C[x0, x1, x2, x3] takové, že pro obraz X zobrazení f platí X = Vproj(f1, f2, ..., fr).
- Ukažte, že homomorfismus f: P1 → X je isomorfismus projektivních algebraických množin.
- Uvažujte šestidimenzionální prostor V tvořený všemi polynomy z C[x,y] stupně nejvýše 2 a odpovídající projektivní prostor P5 tvořený přímkami ve V. Ukažte, že ireducibilní kuželosečky v komplexním afinním prostoru A2 jsou parametrizovány Zariski otevřenou podmnožinou P5 (tedy ireducibilní kuželosečky samy tvoří kvaziprojektivní varietu).
Co bylo probráno
Zde je uveden orientační seznam probrané látky po jednotlivých přednáškách, včetně odkazů do literatury.
- 6. 10. 2017
- Afinní algebraické množiny, Zariského topologie, rozklad noetherovského topologického prostoru na ireducibilní komponenty, algebraické podmnožiny afinní roviny (skripta, kap. 1; [Ful], kap. 1.2, 1.4 - 1.6, 6.1; [Ga], kap. 1.1, 1.3).
- 13. 10. 2017
- Rozklad noetherovského topologického prostoru na ireducibilní komponenty (důkaz), ideál podmnožiny afinního prostoru a charakterizace ireducibility přes prvoideály, polynomiální zobrazení a souřadnicové okruhy (skripta, kap. 1 a 2; [Ful], kap. 1.3, 1.5, 2.1 - 2.2; [Ga], kap. 1.3, 2.1).
- 20. 10. 2017
- Vztah mezi polynomiálními zobrazeními a homomorfismy souřadnicových okruhů, racionální funkce na varietách a funkční tělesa, racionální zobrazení mezi varietami (skripta, kap. 2; [Ful], kap. 2.2, 2.4, 6.6; [Ga], kap. 2.1, 2.3, [Sh], kap. 3).
- 27. 10. 2017
- Vztah mezi racionálními zobrazeními s hustým obrazem a homomorfismy funkčních těles, biracionální ekvivalence, racionální variety (skripta, kap. 2; [Ful], kap. 6.6; [Ga], kap. 2.1, 2.3, 4.3; [Sh], kap. 3).
- 3. 11. 2017
- Racionální rovinné křivky, lokalizace okruhů. (skripta, kap. 2 a 3; [Sh], kap. 3; [AM], kap. 3).
- 10. 11. 2017
- Geometrický význam lokalizace K[X] → K[X]f, radikálové ideály, Hilbertova věta o nulách (skripta, kap. 3; [Ful], kap. 1.7 - 1.10, 6.3; [Ga], kap. 1.2, 2.1; [AM], kap. 7).
- 24. 11. 2017
- Důsledky věty o nulách, otevřená báze Zariského topologie, racionální funkce bez pólů nad algebraicky uzavřeným tělesem jsou polynomiální ([Ful], kap. 1.7, 1.10, 2.4, 6.1; [Ga], kap. 1.2, 2.1).
- 1. 12. 2017
- Lokální okruhy v bodech variety a jejich vlastnosti, rovinné křivky, singulární a nesingulární body na nich, tečny ([Ful], kap. 2.4, 3.1; [Ga], kap. 4.4; text o rovinných křivkách).
- 8. 12. 2017
- Diskrétní valuační obory a charakterizace nesingulárních bodů na rovinných křivkách, ([Ful], kap. 2.5, 3.2; [Ga], kap. 4.4).
- 15. 12. 2017
- Projektivní algebraické množiny, projektivní Zariského topologie, korespondence s homogenními ideály, charakterizace ireducibilních projektivních algebraických množin ([Ful], kap. 2.6, 4.1, 4.2, 4.3; [Ga], kap. 3.1, 3.2).
- 22. 12. 2017
- Projektivní věta o nulách, homogenní souřadnicové okruhy, funkční těleso a regulární funkce na projektivních varietách, homomorfismy mezi projektivními varietami ([Ful], kap. 4.2, 6.3; [Ga], kap. 3.1 - 3.3).
- 5. 1. 2018
- Kartézské součiny afinních i projektivních variet, Segreho vnoření, kvaziprojektivní variety a homomorfismy mezi nimi, projektivní teorie eliminace, na cvičení nafouknutí bodu a řešení singularit ([Ful], kap. 4.4, 6.1 - 6.3, 7.2; [Ga], kap. 2.3, 3.3, 3.4, 4.3).
- 12. 1. 2018
- Homomorfismy z projektivních variet mají uzavřený obraz, Krullova dimenze a její výpočet pro afinní a projektivní prostory, vztah Krullovy dimenze a stupně transcendence funkčního tělesa variety ([Ful], kap. 6.4, 6.5; [Ga], kap. 3.4, 4.1 - 4.2; [Sh], kap. 5.2 - 5.4, 6.1).
Literatura
K přednášce budu v tomto semestru průběžně aktualizovat předběžnou verzi skript: [PDF ke stažení]
Co se další literatury týče, algebraická geometrie postupně vyrostla ve velmi široký obor, o kterém jsou napsány tisíce stránek z různých pohledů. Určitou představu (příp. doporučení, kudy dále pro zájemce) si lze udělat na tomto blogu na mathoverflow.net. Přednáška je inspirována následujícími dvěma zdroji, které jsou volně dostupné on-line v PDF, a proto do nich u seznamu probrané literatury uvádím odkazy:
| [Ga] | A. Gathmann, Algebraic geometry, skripta kurzu z Kaiserslautern, 2002/2003. [PDF ke stažení] |
| [Ful] | W. Fulton, Algebraic Curves (An Introduction to Algebraic Geometry), 2008. [PDF ke stažení] |
Další inspirace a fakta pochází především z těchto (off-line) zdrojů:
| [Sh] | I. R. Shafarevich, Basic algebraic geometry 1, Varieties in projective space, 2. vyd., Springer-Verlag, Berlin, 1994. |
| [AM] | M. F. Atiyah, I. G. MacDonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Co., 1969. |
| [CLO] | D. Cox, J. Little, D. O'Shea, Ideals, varieties, and algorithms, Second Edition, Springer, New York, 2005. |
| [Na] | M. Nagata, Local Rings, John Wiley & Sons, 1962. |
| [Nee] | A. Neeman, Algebraic and Analytic Geometry, LMS Lecture Note Series 345, Cambridge, 2007. |
V češtině lze leccos nalézt i v provizorních skriptech od prof. Drápala:
| [Dr1] | A. Drápal, Komutativní okruhy. [PDF ke stažení] |
| [Dr2] | A. Drápal, Algebraická geometrie - geometrická čast. [PDF ke stažení] |
| [Dr3] | A. Drápal, Algebraická geometrie - algebraická čast. [PDF ke stažení] |
Další odkazy
- Domovská stránka přednášky z Algebraické geometrie ze zimního semestru 2016/2017.
- Domovská stránka přednášky z Algebraické geometrie ze zimního semestru 2015/2016.
- Domovská stránka přednášky z Algebraické geometrie ze zimního semestru 2014/2015.
- Domovská stránka přednášky z Algebraické geometrie ze zimního semestru 2013/2014.