Upozornění: Tato stránka se týkala přednášky v zimním semestru 2014/2015. Odkaz na aktuální přednášku hledejte na domovské stránce.
Základní informace
Sylabus a základní informace viz popis předmětu ve Studijním informačním systému.
Rozvrh (k nalezení též v SISu):
- přednáška ve středu 10:40-12:10 hod. v seminární místnosti KA,
- cvičení ve středu 12:20-13:50 hod. v seminární místnosti KA.
Zkouška
Zkouška je ústní a bude se konat v následujících termínech:
- čtvrtek 15. ledna od 13:00 v seminární místnosti Katedry algebry (odkaz do SISu),
- čtvrtek 5. února od 13:00 v seminární místnosti Katedry algebry (odkaz do SISu),
- čtvrtek 12. února od 13:00 v seminární místnosti Katedry algebry (odkaz do SISu).
Zápočet
Zápočet bude udělován za odevzdané vyřešené příklady. Půjde o tři sady příkladů, které budou vypisovány níže. Požaduji alespoň 50 % vyřešených příkladů v uvedených termínech.
Příklady č. 1 (termín odevzdání 5. listopadu)
- Nechť X1 a X2 jsou algebraické množiny. Ukažtě, že I(X1 ∩ X1) je roven radikálu z I(X1) + I(X2). Najděte příklad, kdy I(X1 ∩ X1) ≠ I(X1) + I(X2).
- Nechť K je algebraicky uzavřené těleso a I ⊆ K[x1, ..., xn] je ideál. Ukažte, že radikál ideálu I je roven průniku všech maximálních ideálů K[x1, ..., xn], které I obsahují.
- Najděte generátory maximálního ideálu M okruhu R[x,y] polynomů nad reálnými čísly, který má nulu v bodě (3 + 2i, 5 - 4i) ∈ A².
- Nechť C je těleso komplexních čísel a X ⊆ A3 je sjednocení všech tří os x, y a z. Najděte generátory ideálu I(X) ⊆ C[x,y,z].
Příklady č. 2 (termín odevzdání 10. prosince)
- C-algebraickou podmnožinu X ⊆ A2 nazveme kuželosečkou, pokud je tvaru X = V({f(x,y)}), kde f(x,y) je nenulový polynom celkového stupně 2. Ukažte, že každá ireducibilní kuželosečka je isomorfní buď V({y-x2}) nebo V({xy-1}).
- Nechť X = V({x3 + y3 - 3x2 - 3y2 +3xy +1}) je rovinná křivka definovaná nad tělesem komplexních čísel. Najděte všechny násobné body X a v těchto násobných bodech všechny tečné přímky.
- Nechť X = V({y2 - x3}) je C-algebraická podmnožina A2 a uvažujte regulární funkci r: X \ {(0,0)} → A1 danou předpisem r(a,b) = b/a. Lze r rozšířit na regulární funkci na celém X? Proč?
Příklady č. 3 (termín odevzdání 12. ledna)
-
Nechť K je algebraicky uzavřené těleso. Definujeme zobrazení i z množiny dvoudimenzionálních podprostorů V ⊆ K4 do projektivního prostoru P5 následovně. Vezmeme ve V libovolné dva lineárně nezávislé vektory v = (a0, a1, a2, a3) a w = (b0, b1, b2, b3), jejich složky zapíšeme do matice 2x4
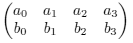
a spočítáme (v nějakém pevném pořadí) všech 6 determinantů d0, d1, ..., d5 podmatic velikosti 2x2. Pak i bude zobrazovat V na (d0 : d1 : ... : d5).
- Ukažte, že i je dobře definované prosté zobrazení.
- Ukažte, že obraz G zobrazení i je projektivní varieta zadaná v P5 jednou kvadratickou rovnicí.
- Ukažte, že G lze jakožto abstraktní varietu pokrýt 6 otevřenými podmnožinami isomorfními A4.
(Nápověda: Použijte na matici 2x4 Gaussovu eliminaci.)
- Uvažujte šestidimenzionální podprostor V všech polynomů z C[x,y] stupně nejvýše 2 a odpovídající projektivní prostor P5 tvořený přímkami ve V. Ukažte, že ireducibilní kuželosečky v komplexním afinním prostoru A2 jsou parametrizovány Zariski otevřenou podmnožinou P5.
Co bylo probráno
Zde je uveden orientační seznam probrané látky po jednotlivých přednáškách, včetně odkazů do literatury.
- 1. 10. 2014
- Afinní algebraické množiny, přiřazení V a I, Zariského topologie ([Ful], kap. 1.2, 1.3, 6.1).
- 8. 10. 2014
- Rozklad noetherovského topologického prostoru na ireducibilní komponenty, algebraické variety, polynomiální zobrazení a souřadnicové okruhy ([Ful], kap. 1.5, 2.1, 2.2; [Ga], kap. 1.3).
- 15. 10. 2014
- Vztah mezi polynomiálními zobrazeními a homomorfismy souřadnicových okruhů, lokalizace okruhů ([Ful], kap. 2.2, [AM], kap. 3).
- 22. 10. 2014
- Hilbertovy věty o nulách, charakterizace souřadnicových okruhů mezi algebrami, maximální ideály souřadnicových okruhů ([Ful], kap. 1.7, 1.10; [Ga], kap. 1.2).
- 29. 10. 2014
- Standardní báze Zariského topologie, geometrický význam lokalizace K[X]f, regulární funkce ([Ful], kap. 2.4, 6.1, 6.2; [Ga], kap. 2.1).
- 5. 11. 2014
- Popis algebry regulárních funkcí na bázových otevřených množinách Zariského topologie ([Ful], kap. 2.4, [Ga], kap. 2.1, [Nee], lemmata 3.4.14 a 3.4.15).
- 19. 11. 2014
- Lokální okruhy v bodech algebraické množiny ([Ful], kap. 2.4, [Ga], kap. 2.1).
- 26. 11. 2014
- Kotečný prostor, afinní rovinné křivky, charakterizace jednoduchých bodů na rovinných křivkách pomocí lokálních okruhů ([Ful], kap. 2.9, 3.1, 3.2).
- 3. 12. 2014
- Dokončení charakterizace jednoduchých bodů na rovinných křivkách, (ne)singulární body na algebraických množinách vyšších dimenzí, svazky K-algeber, okruhované prostory ([Ful], kap 3.2, [Ga], kap. 2.2, 4.4).
- 10. 12. 2014
- Homomorfismy okruhovaných prostorů, abstraktní algebraické množiny a variety ([Ga], kap. 2.3 - 2.5, [Nee], kap. 2).
- 17. 12. 2014
- Abstraktní algebraické variety a kritérium přes uzavřenost diagonály Δ(X) produktu X x X, projektivní algebraické variety, projektivní věta o nulách ([Ga], kap. 2.5, 3.1, 3.2, [Ful], kap. 4.1, 4.2).
- 7. 1. 2015
- Projektivní algebraické množiny coby abstraktní algebraické množiny, uzavřenost morfismů z projektivních algebraických množin, zběžně Krullova dimenze ([Ga], kap. 3.3, 3.4, 4.1).
Literatura
Jde stále o novou přednášku, ke které zatím skripta nejsou k dispozici. Algebraická geometrie je velmi široký obor, o kterém jsou napsány tisíce stránek z různých pohledů. Určitou představu (příp. doporučení, kudy dále pro zájemce) si lze udělat na tomto blogu na mathoverflow.net. Jádro přednášky je prezentováno podle následujících dvou zdrojů, které jsou dostupné on-line v PDF:
| [Ga] | A. Gathmann, Algebraic geometry, skripta kurzu z Kaiserslautern, 2002/2003. [PDF ke stažení] |
| [Ful] | W. Fulton, Algebraic Curves (An Introduction to Algebraic Geometry), 2008. [PDF ke stažení] |
Přednášené výsledky jsou doplněny o některá fakta z komutativní algebry, která jsou k nalezení v následujících (off-line) zdrojích:
| [AM] | M. F. Atiyah, I. G. MacDonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Co., 1969. |
| [CLO] | D. Cox, J. Little, D. O'Shea, Ideals, varieties, and algorithms, Second Edition, Springer, New York, 2005. |
| [Na] | M. Nagata, Local Rings, John Wiley & Sons, 1962. |
| [Nee] | A. Neeman, Algebraic and Analytic Geometry, LMS Lecture Note Series 345, Cambridge, 2007. |
V češtině lze leccos nalézt i v provizorních skriptech od prof. Drápala:
| [Dr1] | A. Drápal, Komutativní okruhy. [PDF ke stažení] |
| [Dr2] | A. Drápal, Algebraická geometrie - geometrická čast. [PDF ke stažení] |
| [Dr3] | A. Drápal, Algebraická geometrie - algebraická čast. [PDF ke stažení] |