Algebraic Geometry [Jan Stovicek]

Warning: This web page is about the course in winter semester 2014/2015. Please check the home page for information about the current course.

Basic information

The contents of the course and other basic information are available in the Student Information System.

The schedule (to be found also in the Student Information System):

lectures on Wednesdays, 10.40am-12.10pm in the seminar room of the Department of Algebra,
problem sessions on Wednesdays, 12.20pm-1.50pm in the seminar room of the Department of Algebra.

Exam

The exam will be oral and will take place on:

Thursday January 15th at 1pm in the seminar room of Dept. Alg. (link to SIS),
Thursday February 5th at 1pm in the seminar room of Dept. Alg. (link to SIS),
Thursday February 12th at 1pm in the seminar room of Dept. Alg. (link to SIS).

Credit

The credit will be granted for solved exercise problems. There will be three sets of the problems and they will appear here. Requested are at least 50% of successfully solved problems handed in withing the deadlines.

Problem set #1 (deadline for solutions: November 5)

Let X₁ and X₂ be algebraic sets. Show that I(X₁ ∩ X₁) is equal to the radical of I(X₁) + I(X₂). Find an example where I(X₁ ∩ X₁) ≠ I(X₁) + I(X₂).
Let K be an algebraically closed field and I ⊆ K[x₁, ..., x_n] be an ideal. Show that the radical of I is equal to the intersection of the maximal ideals of K[x₁, ..., x_n] which contain I.
Find generators of the maximal ideal M of the ring R[x,y] of polynomials over the real numbers which has zero at (3 + 2i,5 - 4i) ∈ A².
Let C be the field of complex numbers and let X ⊆ A³ be the union of the three coordinate axes. Find generators for the ideal I(X) ⊆ C[x,y,z].

Problem set #2 (deadline for solutions: December 10)

A C-algebraic subset X ⊆ A² is called a conic if it is of the form X = V({f(x,y)}) where f(x,y) is a non-zero polynomial of total degree 2. Show that every irreducible conic is isomorphic either to V({y-x²}) or to V({xy-1}).
Let X = V({x³ + y³ - 3x² - 3y² +3xy +1}) be an affine curve defined over the field of complex numbers. Find all multiple points of X and all tangent lines at these multiple points.
Consider the C-algebraic subset X = V({y² - x³}) of A² and the regular function r: X \ {(0,0)} → A¹ given by r(a,b) = b/a. Is it possible to extend r to a regular function defined everywhere on X? Why?

Problem set #3 (deadline for solutions: January 12)

Let K be an algebraically closed field. We shall define a map i from the set of 2-dimesional subspaces V ⊆ K⁴ to the projective space P⁵ as follows. We arbitrarily choose two linearly independent vectors v = (a₀, a₁, a₂, a₃) and w = (b₀, b₁, b₂, b₃) in V, we write the components into a 2x4 matrix

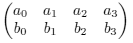
$\begin{pmatrix} a_0 & a_1 & a_2 & a_3 \\ b_0 & b_1 & b_2 & b_3 \end{pmatrix}$

and we compute (in any fixed order) the 6 determinants d₀, d₁, ..., d₅ of all 2x2 submatrices. Then we define i to map V to (d₀ : d₁ : ... : d₅).
1. Show that i is a well defined injective map.
2. Show that the image G of i is a projective variety given in P⁵ by a single quadratic equation.
3. Show that we can cover G (as an abstract variety) by 6 open subsets isomorphic to A⁴.
(Hint: Apply Gauss elimination to the 2x4 matrix.)
Consider the 6-dimensional subspace V of C[x,y] consisting of all polynomials of total degree at most 2. Consider also the corresponding projective space P⁵ whose elements are lines in V. Show that the irreducible conics in the complex affine space A² are parametrized by a Zariski open subset of P⁵.

What has been lectured

A brief overview of what has been taught in individual lectures, including references to the literature, can be found below.

October 1, 2014: Affine algebraic sets, the assignments V and I, Zariski topology ([Ful], sec. 1.2, 1.3, 6.1).
October 8, 2014: The decomposition of a noetherian topological space to irreducible components, algebraic varieties, polynomial maps and coordinate rings ([Ful], sec. 1.5, 2.1, 2.2; [Ga], sec. 1.3).
October 15, 2014: The connection between polynomial maps and homomorphisms of coordinate rings, localization of rings ([Ful], sec. 2.2, [AM], ch. 3).
October 22, 2014: Hilbert's Nullstellensatz, a characterization of coordinate rings among algebras, maximal ideals of coordinate rings ([Ful], sec. 1.7, 1.10, [Ga], sec. 1.2).
October 29, 2014: The standard basis of the Zariski topology, a geometric interpretation of the localization K[X]_f, regular functions ([Ful], sec. 2.4, 6.1, 6.2; [Ga], sec. 2.1).
November 5, 2014: A description of the algebra of regular functions on basic Zariski open sets ([Ful], sec. 2.4, [Ga], sec. 2.1, [Nee], Lemmas 3.4.14 and 3.4.15).
November 19, 2014: Local rings at points of an algebraic set ([Ful], sec. 2.4, [Ga], sec. 2.1).
November 26, 2014: Cotangent spaces, affine plane curves, a characterization of simple points of plane curves in terms of local rings ([Ful], sec. 2.9, 3.1, 3.2).
December 3, 2014: Finishing the characterization of simple points of plane curves, (non)singular points of algebraic sets of higher dimension, sheaves of K-algebras, ringed spaces ([Ful], sec 3.2, [Ga], sec. 2.2, 4.4).
December 10, 2014: Homomorphisms of ringed spaces, abstract algebraic sets and varieties ([Ga], sec. 2.3 - 2.5, [Nee], chapter 2).
December 17, 2014: Abstract algebraic varieties and the criterion on the diagonal Δ(X) of X x X, projective algebraic varieties, projective Nullstellensatz ([Ga], sec. 2.5, 3.1, 3.2, [Ful], sec. 4.1, 4.2).
January 7, 2015: Projective algebraic sets as abstract algebraic sets, closedness of morphisms from projective algebraic sets, a brief introduction to Krull dimension ([Ga], sec. 3.3, 3.4, 4.1).

Literature

This is still a recently introduced course and with no lecture notes available specifically for it yet. Algebraic geometry is a very broad field with thousands of pages written about it from several points of view. To get an impression (or to get an idea where to go next for those interested in the topic), check this blog on mathoverflow.net. The core of the lecture is presented according to the following sources available in PDF:

[Ga]	A. Gathmann, Algebraic geometry, notes from a course in Kaiserslautern, 2002/2003. [Full text in PDF]
[Ful]	W. Fulton, Algebraic Curves (An Introduction to Algebraic Geometry), 2008. [Full text in PDF]

The lectures also involve some facts from commutative algebra which can be found in the following (off-line) sources:

[AM]	M. F. Atiyah, I. G. MacDonald, Introduction to Commutative Algebra, Addison-Wesley Publishing Co., 1969.
[CLO]	D. Cox, J. Little, D. O'Shea, Ideals, varieties, and algorithms, Second Edition, Springer, New York, 2005.
[Na]	M. Nagata, Local Rings, John Wiley & Sons, 1962.
[Nee]	A. Neeman, Algebraic and Analytic Geometry, LMS Lecture Note Series 345, Cambridge, 2007.

Algebraic Geometry · Jan Stovicek