Goniometrické funkcie
Úloha 1
Priraď správnu funkčnú hodnotu:
| A | B | C | D | E | F | G | H | ||
| \({\sqrt{3} \over 3}\) | \({\sqrt{3} \over 2}\) | \({\sqrt{2} \over 2}\) | \(-1\) | \(0\) | \({1 \over 2}\) | \(1\) | \(\sqrt{3}\) | ||
| a) \(\sin \large {\pi \over 6}\) | |||||||||
| b) \(\cos \large {\pi \over 4}\) | |||||||||
| c) \({\rm tg}\: \large {\pi \over 3}\) | |||||||||
| d) \({\rm cotg}\: \large {\pi \over 3}\) | |||||||||
| e) \(\sin \large {3\pi \over 2}\) | |||||||||
| f) \(\cos \large {\pi \over 6}\) | |||||||||
| g) \({\rm tg}\: \pi \) | |||||||||
| h) \({\rm cotg}\: \large {\pi \over 4}\) |
Úloha 2
Urči riešenie danej rovnice s neznámou \(x \in \mathbb{R}\):
a)\(\cos x = -1\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ 0 + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ -{\pi \over 2} + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ -\pi + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ -{\pi \over 2} + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ -\pi + 2k\pi \right \}\)
b)\(\sin x = {\sqrt{3} \over 2}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 6} + 2k\pi; {5 \over 6}\pi + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 3} + 2k\pi; {2 \over 3}\pi + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 4} + 2k\pi; {3 \over 4}\pi + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 3} + 2k\pi; {2 \over 3}\pi + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 4} + 2k\pi; {3 \over 4}\pi + 2k\pi \right \}\)
c)\({\rm tg}\: x = 1\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 2} + k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 4} + k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 2} + k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 4} + k\pi \right \}\)
d)\({\rm cotg}\: x = -1\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {3 \over 4}\pi + 2k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ -{\pi \over 4} + k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 4} + k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ -{\pi \over 4} + k\pi \right \}\)
\(K = \bigcup\limits_{k\in\mathbb{Z}} \left \{\ {\pi \over 4} + k\pi \right \}\)
Úloha 3
Zisti akému zadaniu odpoveda červenou farbou vyznačené riešenie na jednotkovej kružnici.
a)
\(\sin x \geq {1 \over 2}\)
\(\cos x > {1 \over 2}\)
\(\sin x > {1 \over 2}\)
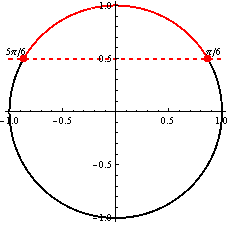
\(\cos x > {1 \over 2}\)
\(\sin x > {1 \over 2}\)
b)
\(\sin x \leq 0\)
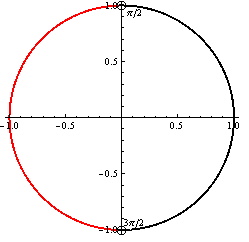
\(\cos x > 0\)
\(\cos x < 0 \)
\(\cos x > 0\)
\(\cos x < 0 \)
c)
\(\cos x \leq 1\)
\({\rm tg}\: x \leq 1\)
\({\rm cotg}\: x \leq 1 \)
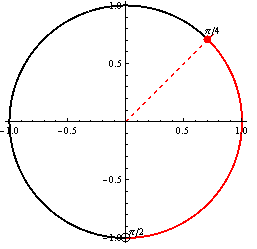
\({\rm tg}\: x \leq 1\)
\({\rm cotg}\: x \leq 1 \)
Úloha 4
Rozhodni, či dané tvrdenie je pravdivé:
| a) \(\sin {\pi \over 6} = {1 \over 2}\) |  |
 |
|
| b) Funkcia sínus je pre \(x \in \mathbb{R}\) nepárna. | |
|
|
| c) Funkcia tangens je pre \(x \in \mathbb{R}\) neohraničená. | |
|
|
| d) Funkcia kotangens je pre \(x \in \mathbb{R}\) rastúca na celom definičnom obore. | |
|
|
| e) Funkcia kosínus je pre \(x \in \mathbb{R}\) neohraničená. | |
|
|
| f) \(\cos 180^\circ = -1\) | |
|
|
| g) \(\rm tg {\large\pi \over 2} = 0\) | |
|
|
| h) \({\rm cotg}\: x = \large{\frac {\sin x} {\cos x}}\) | |
|
Úloha 5
Zisti predpis funkcie, ktorá je vykreslená na obrázku!
a)
\(y = 2{\rm sin}\: x - 1 \)
\(y = 2{\rm cos}\: x - 1 \)
\(y = 2{\rm cos}\: x \)
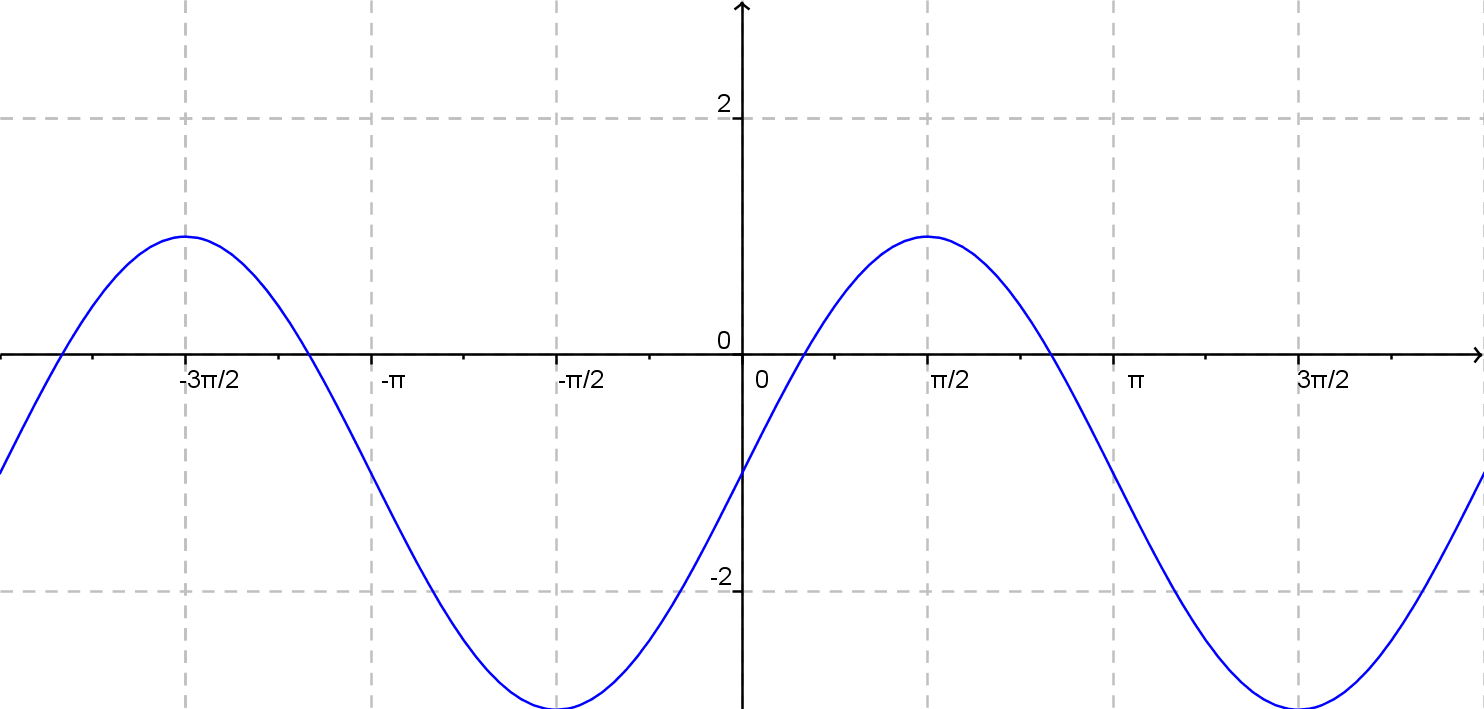
\(y = 2{\rm cos}\: x - 1 \)
\(y = 2{\rm cos}\: x \)
b)
\(y = |{\rm sin}\: x | - \frac {1}{2} \)
\(y = |{\rm sin}\: x - 1 | \)
\(y = |{\rm sin}\: x - \frac {1}{2} | \)
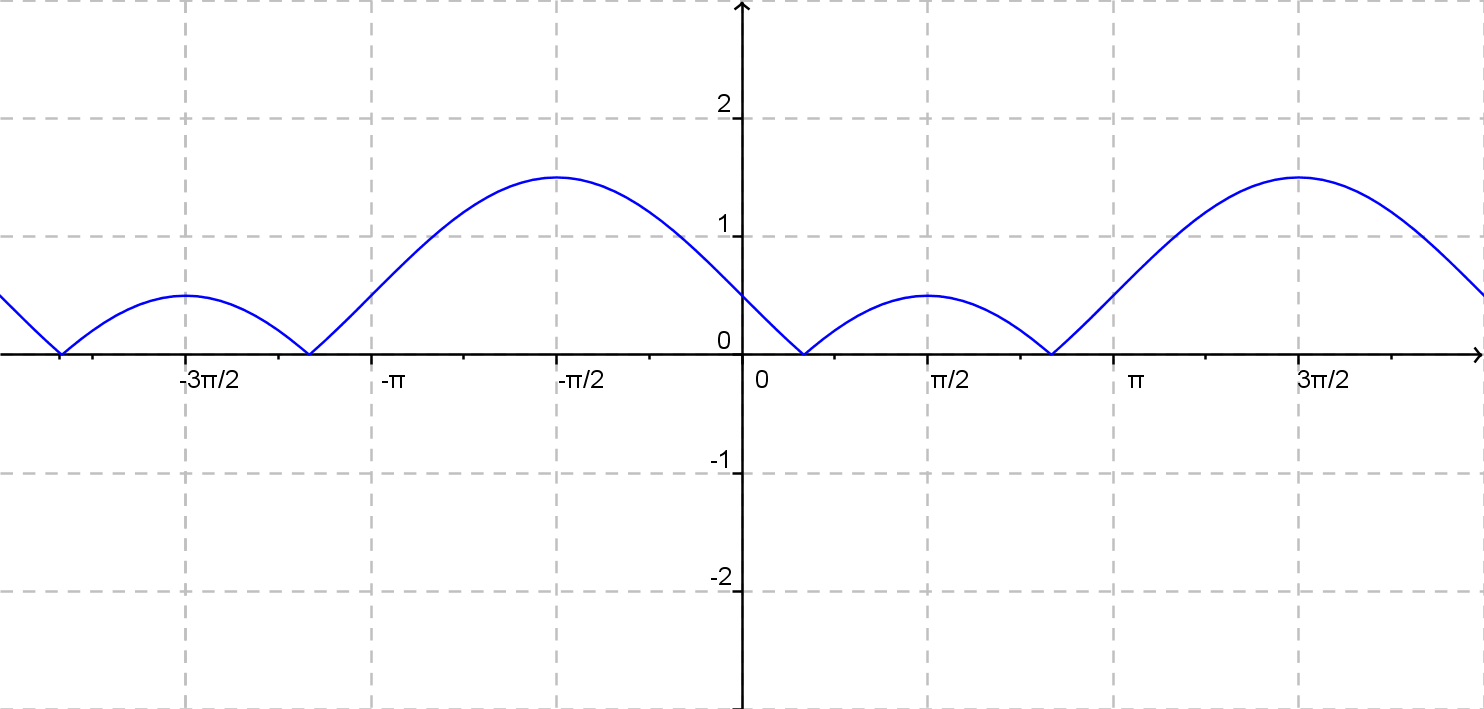
\(y = |{\rm sin}\: x - 1 | \)
\(y = |{\rm sin}\: x - \frac {1}{2} | \)
c)
\(y = {\rm cos}\: (x + \frac {\pi}{6})\)
\(y = {\rm cos}\: (x + \frac {\pi}{4})\)
\(y = {\rm cos}\: (x + \frac {\pi}{3})\)
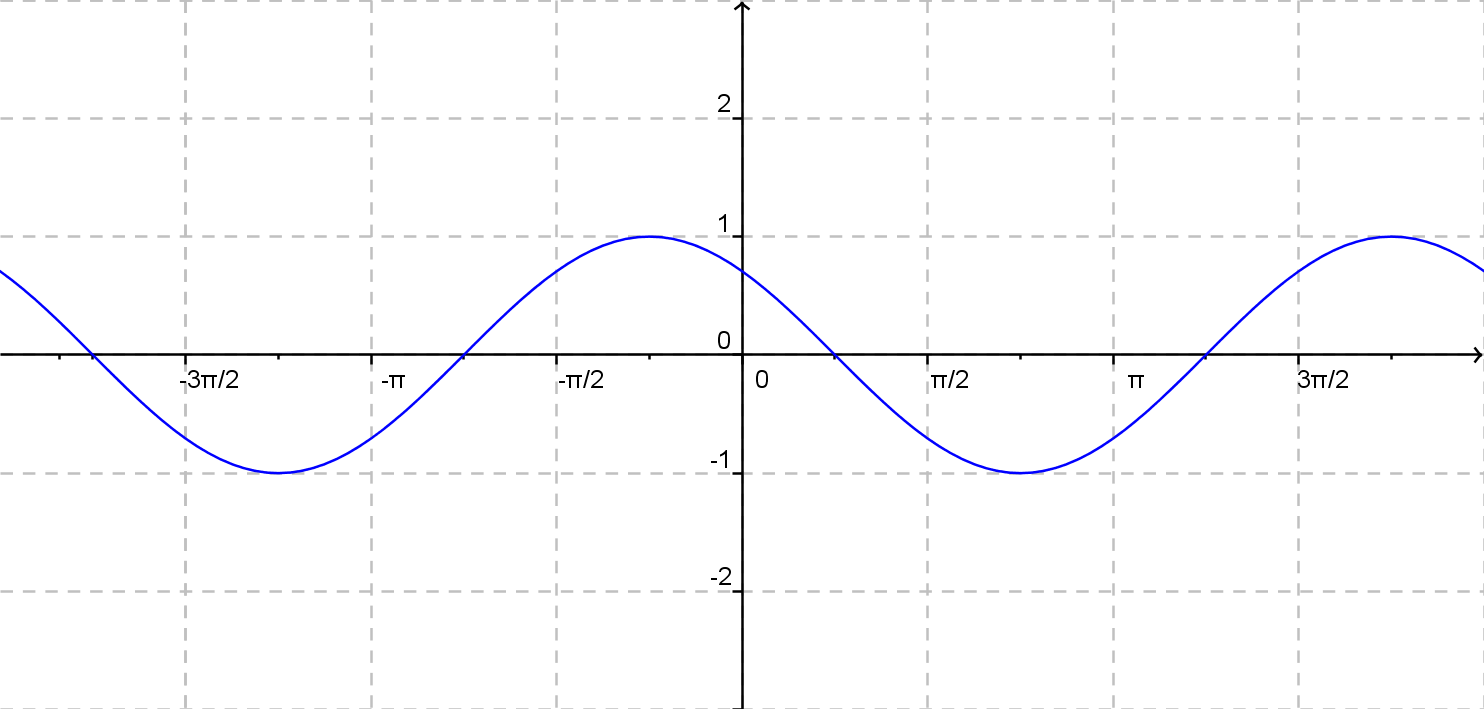
\(y = {\rm cos}\: (x + \frac {\pi}{4})\)
\(y = {\rm cos}\: (x + \frac {\pi}{3})\)
d)
\(y = {\rm cos}\: (x + \frac {\pi}{4}) - 1\)
\(y = {\rm cos}\: (x + \frac {\pi}{3}) - 1\)
\(y = {\rm cos}\: (x + \frac {\pi}{6}) - 1\)
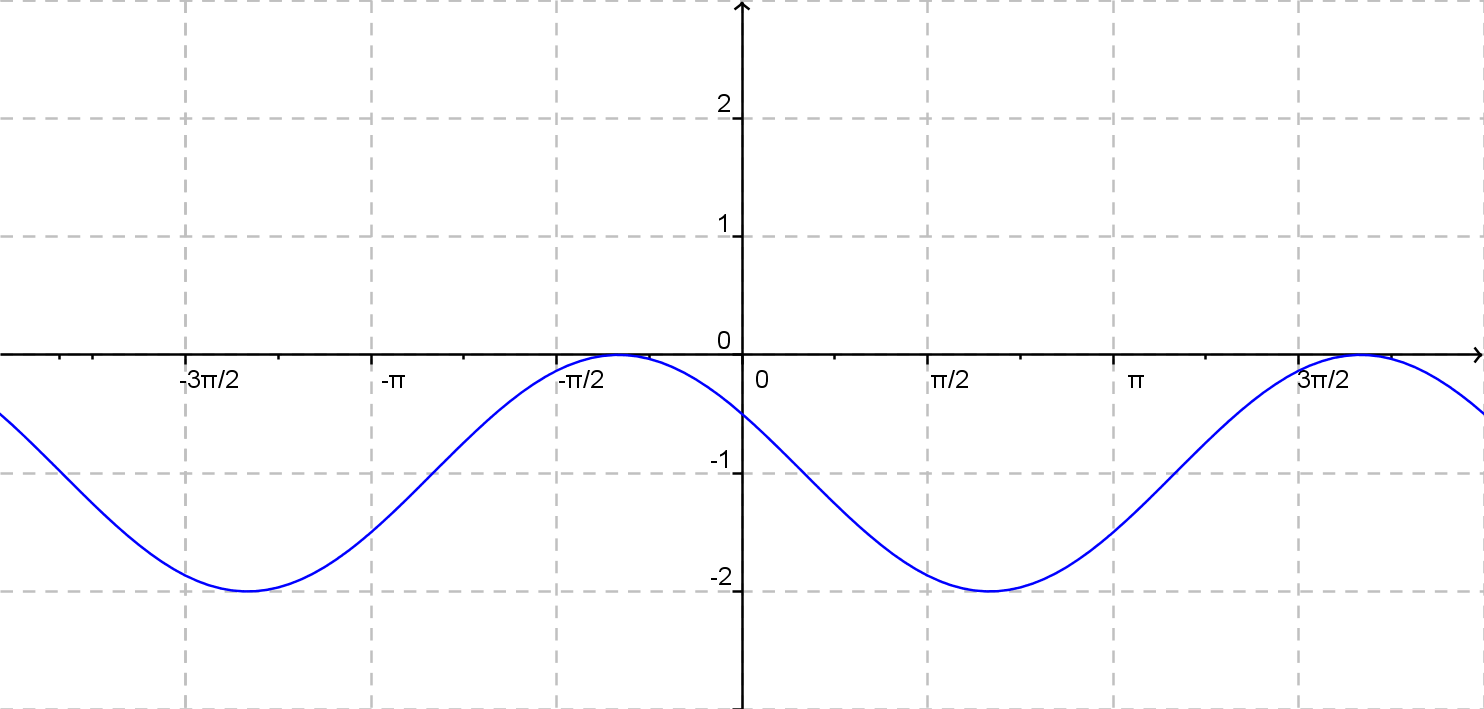
\(y = {\rm cos}\: (x + \frac {\pi}{3}) - 1\)
\(y = {\rm cos}\: (x + \frac {\pi}{6}) - 1\)
e)
\(y = 2{\rm tg}\: x - 1\)
\(y = {\rm tg}\: x - 1\)
\(y = 2{\rm tg}\: x \)
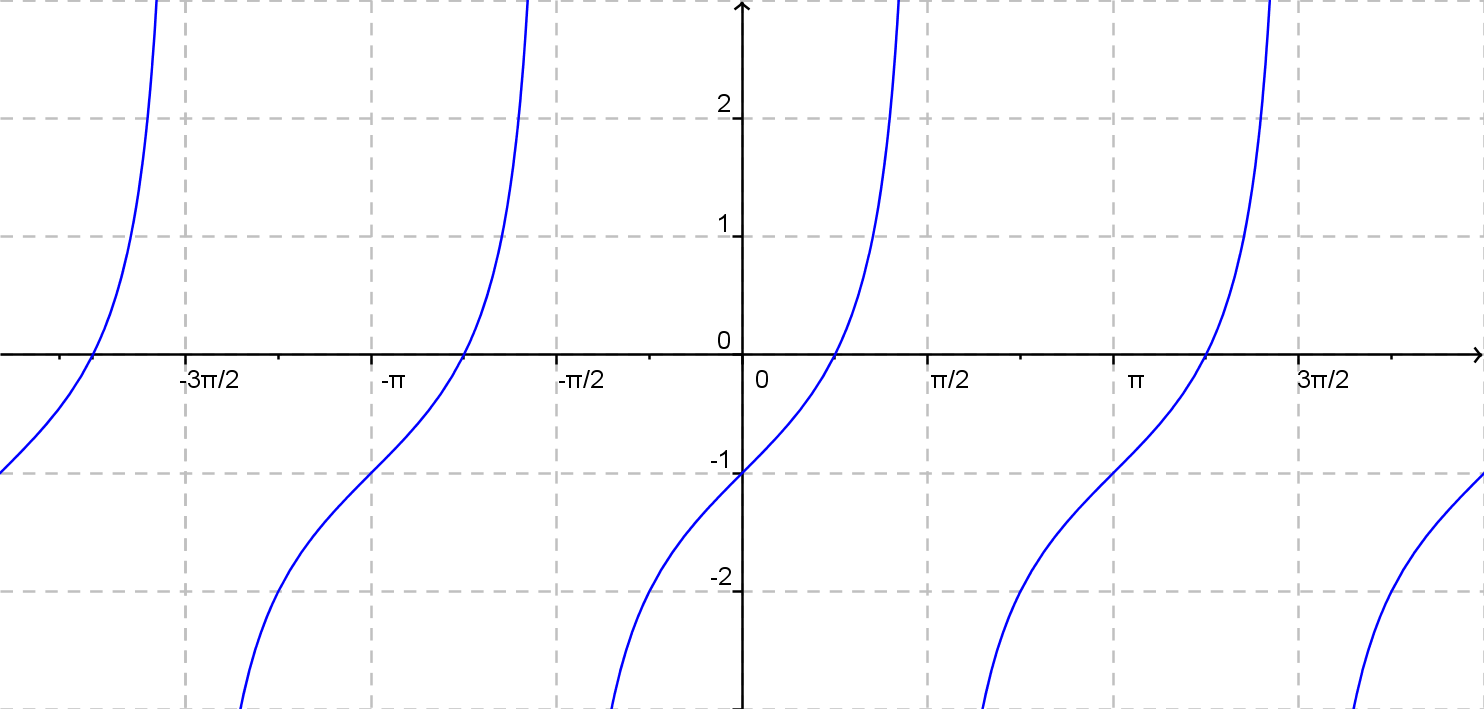
\(y = {\rm tg}\: x - 1\)
\(y = 2{\rm tg}\: x \)
f)
\(y = {\rm tg}\: (x + \frac {\pi}{3})\)
\(y = {\rm tg}\: (x + \frac {\pi}{4})+ 1\)
\(y = {\rm tg}\: (x + \frac {\pi}{3})+ 1\)
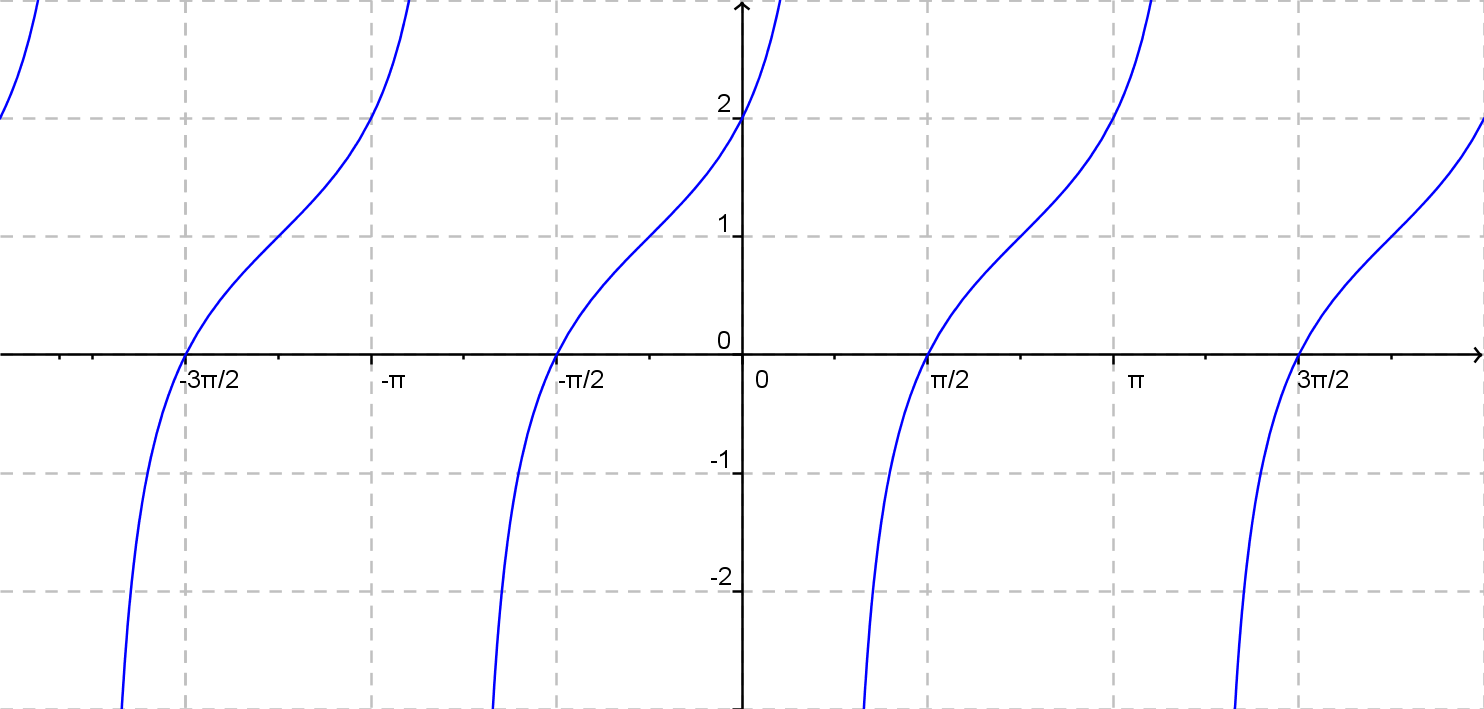
\(y = {\rm tg}\: (x + \frac {\pi}{4})+ 1\)
\(y = {\rm tg}\: (x + \frac {\pi}{3})+ 1\)
g)
\(y = 1 - {\rm cotg}\: x \)
\(y = 2 - {\rm cotg}\: x \)
\(y = {\rm cotg}\: x \)
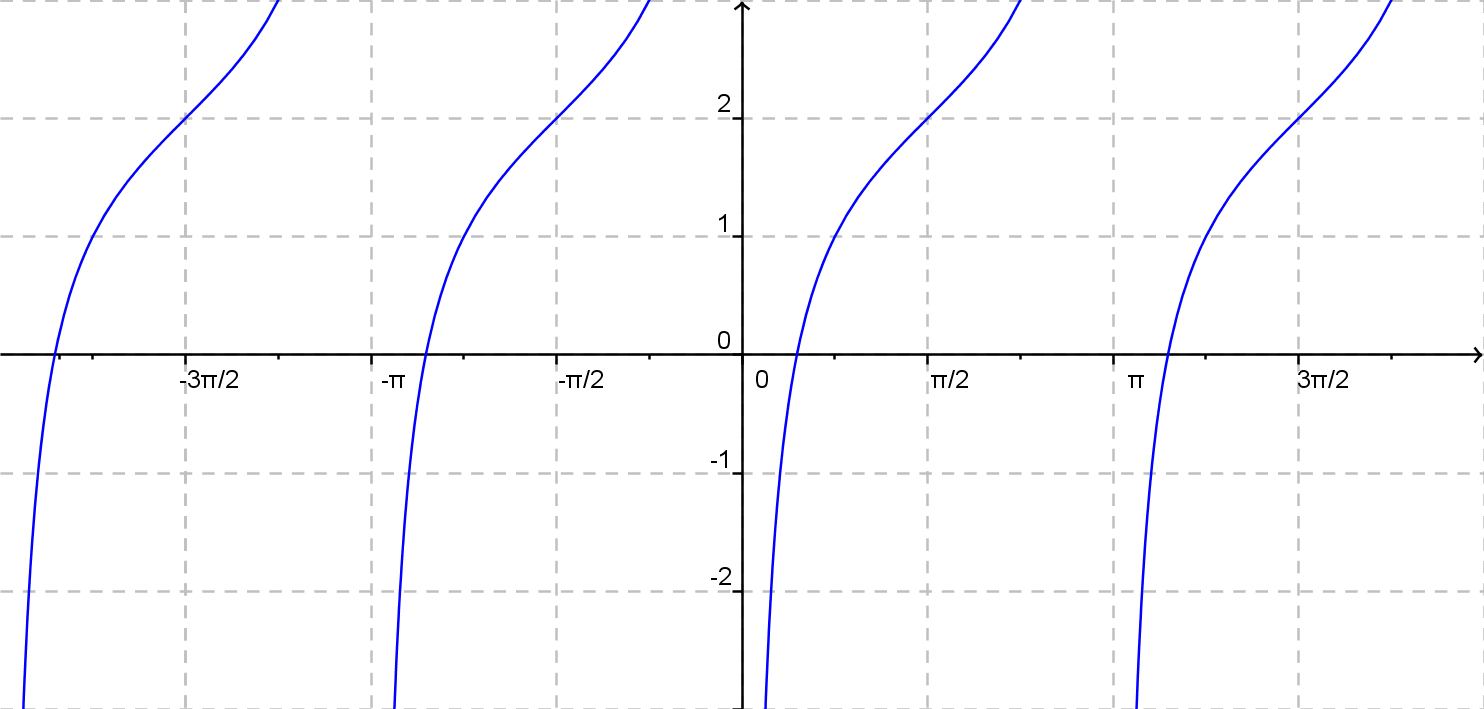
\(y = 2 - {\rm cotg}\: x \)
\(y = {\rm cotg}\: x \)
h)
\(y = |{\rm cotg}\: x - 1 |\)
\(y = |{\rm cotg}\: x + 1 |\)
\(y = 2|{\rm cotg}\: x - 1 |\)
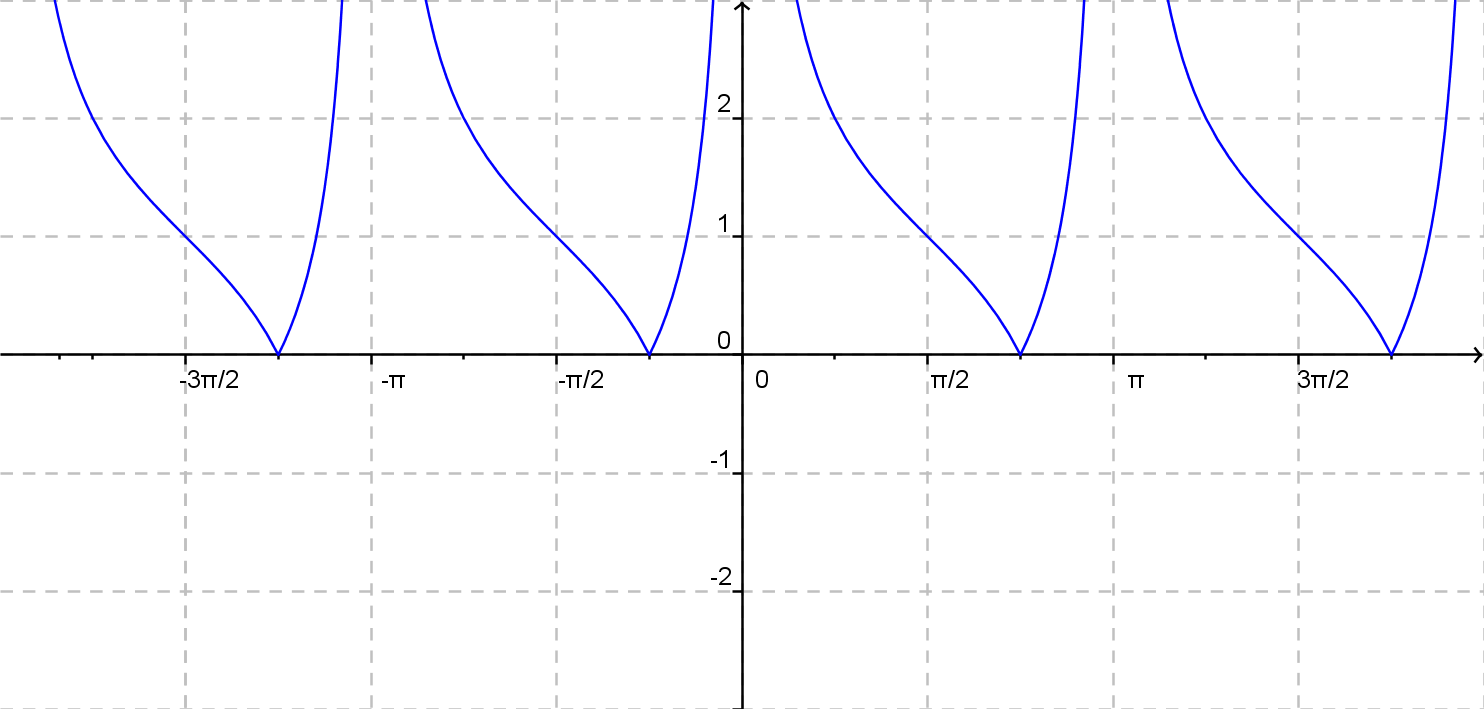
\(y = |{\rm cotg}\: x + 1 |\)
\(y = 2|{\rm cotg}\: x - 1 |\)
Úloha 6
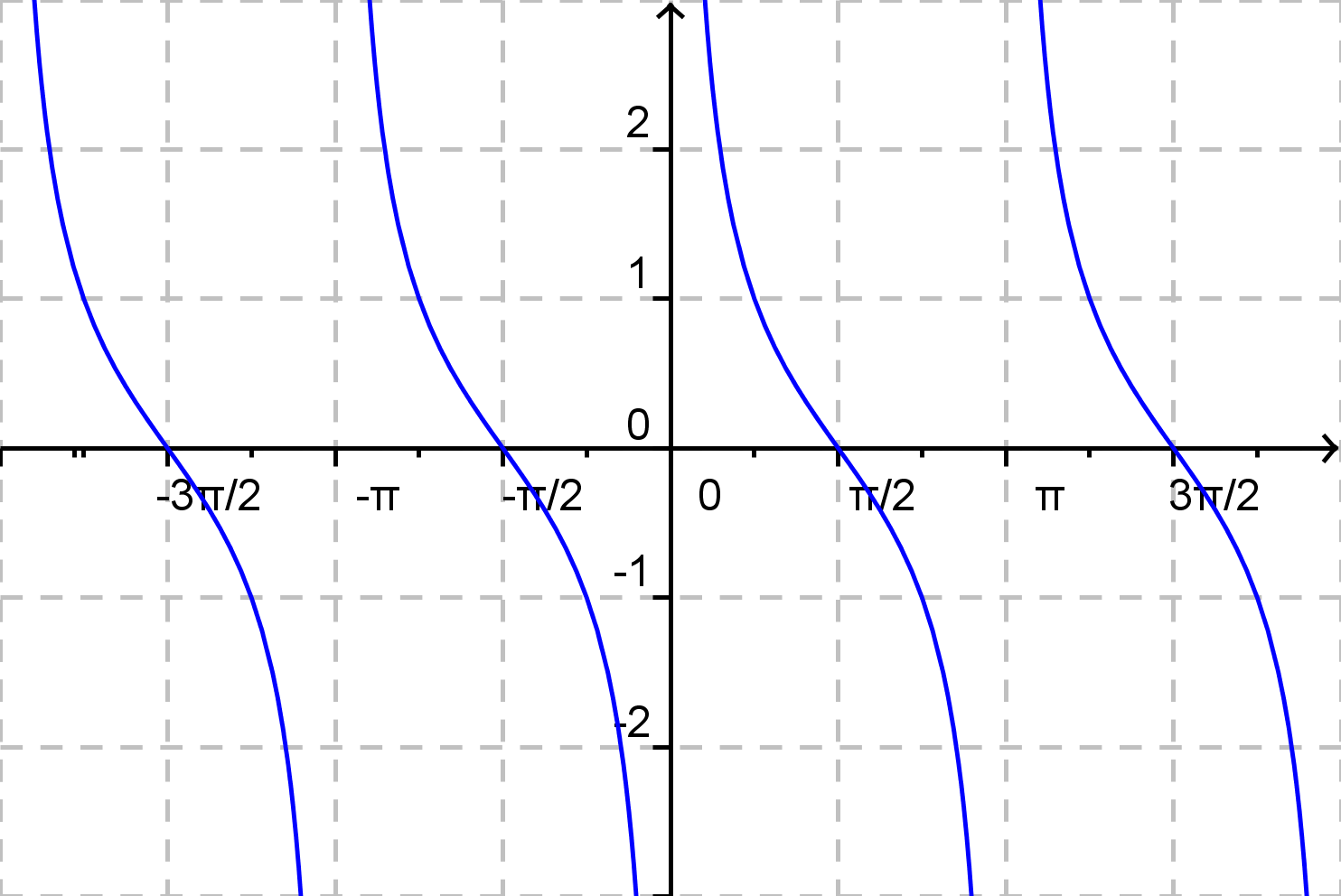
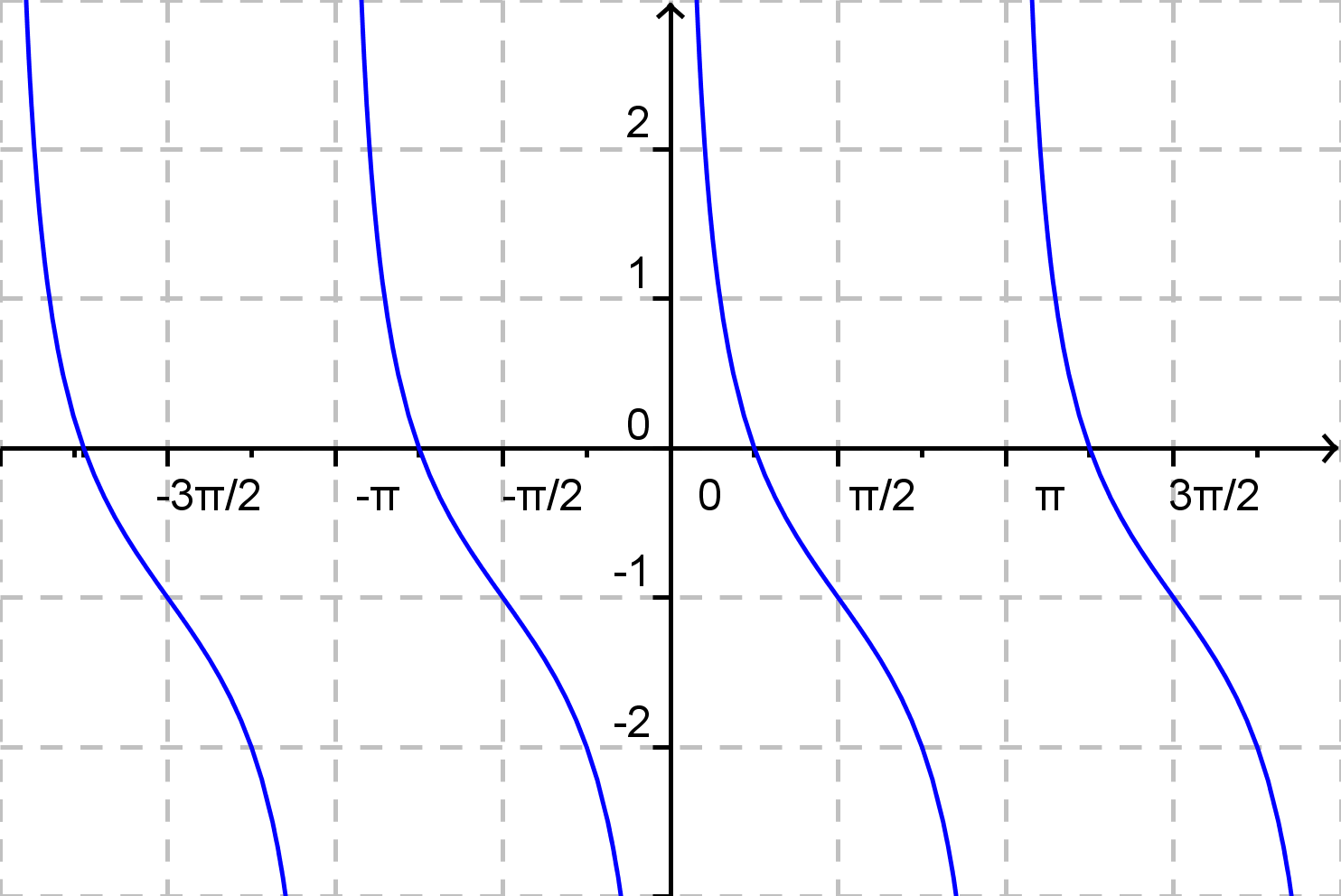
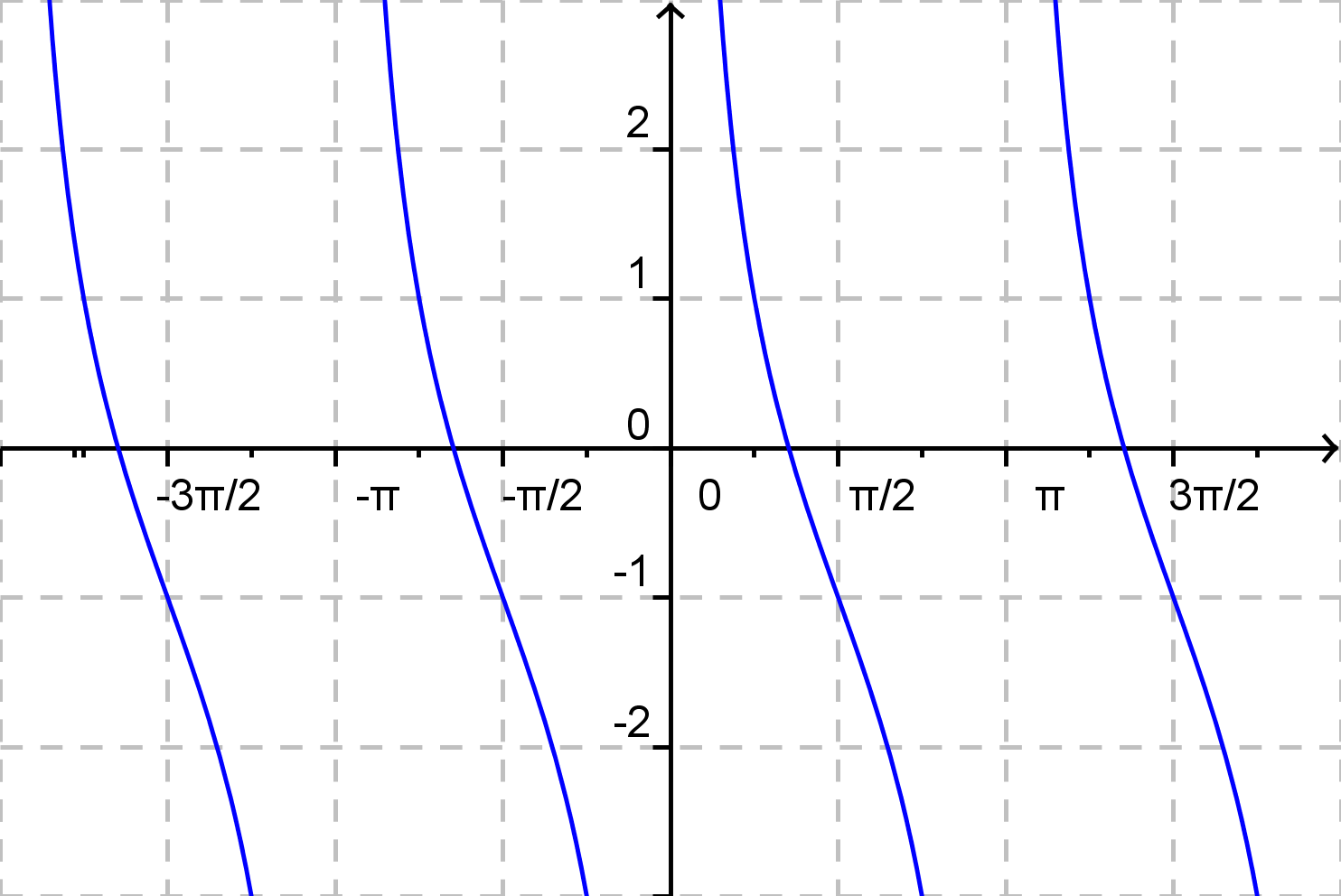
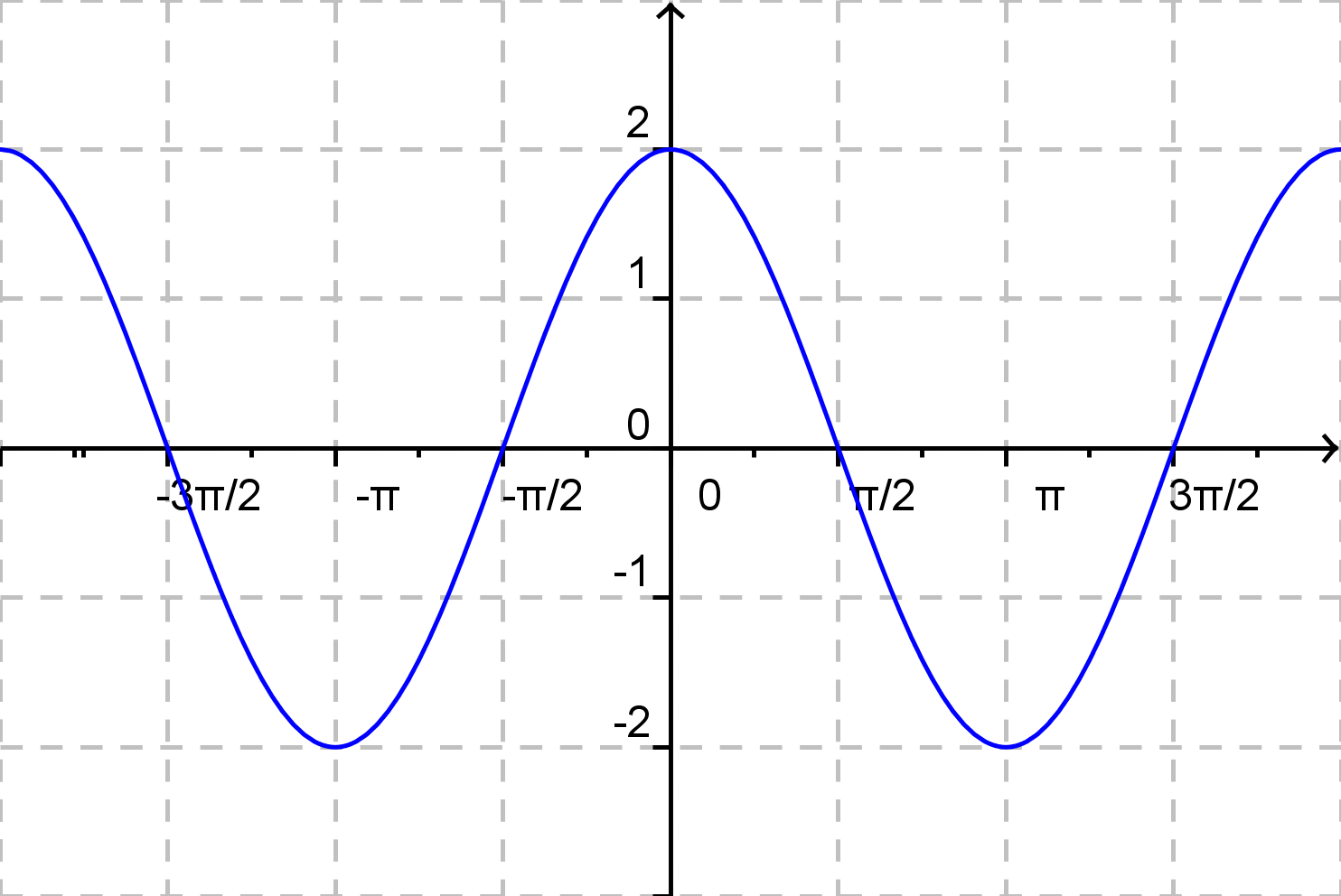
Zisti, ktorý graf odpovedá zadanému predpisu funkcie!
a)
\( f(x) = |{\rm sin}\: x + \frac {\pi}{6} | \)
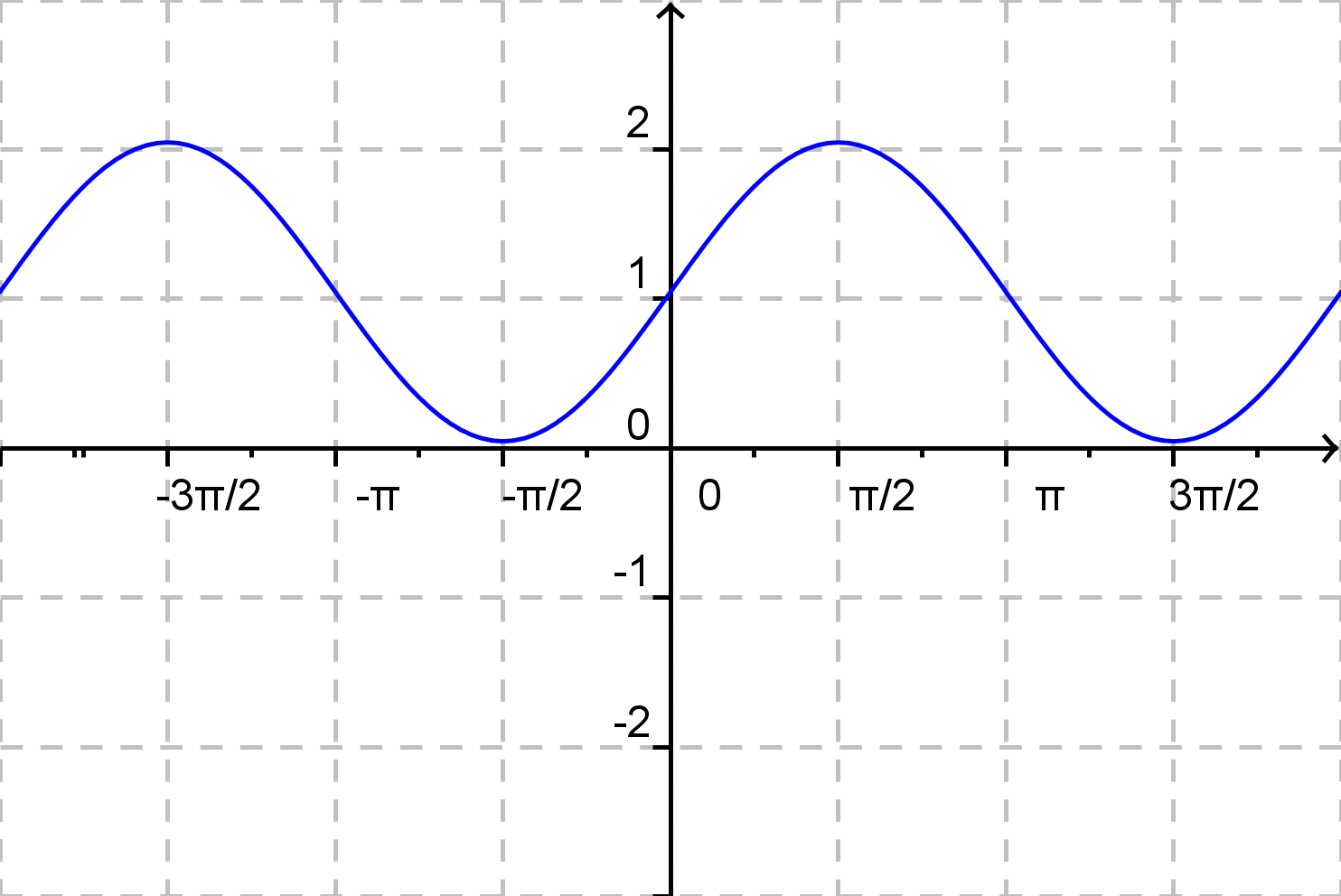
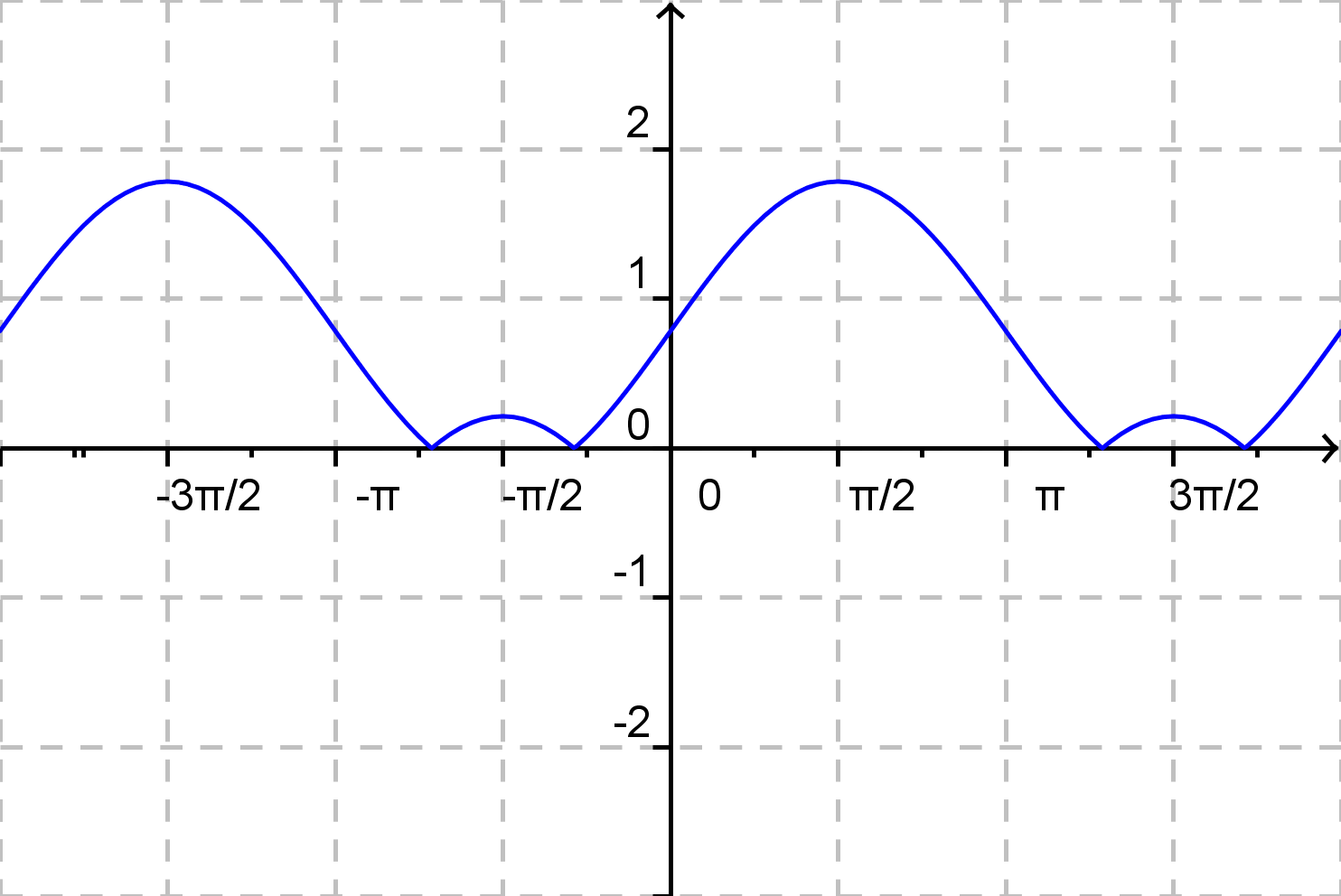
b)
\( f(x) = 2{\rm cos}\: x + \frac {\pi}{4} \)
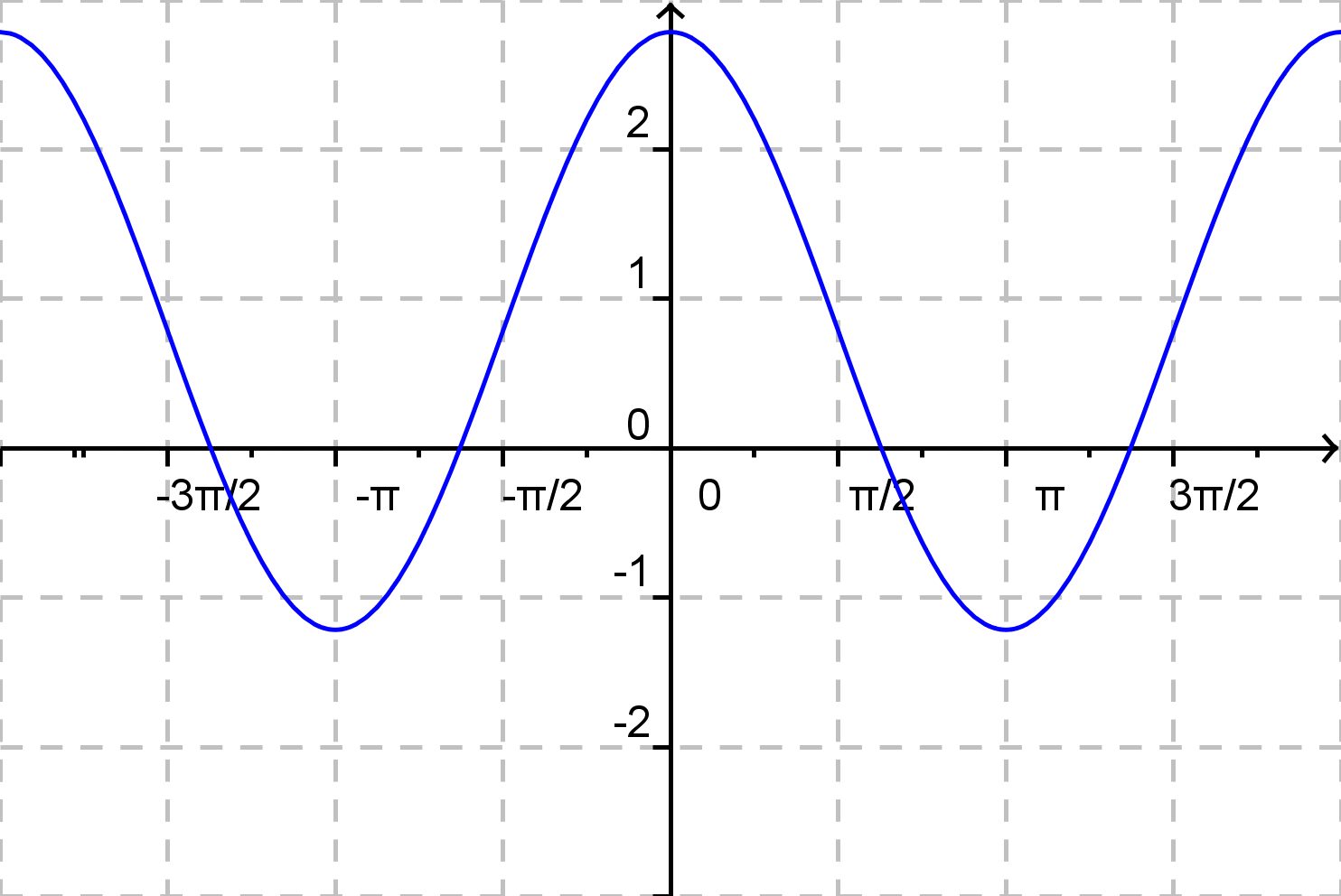
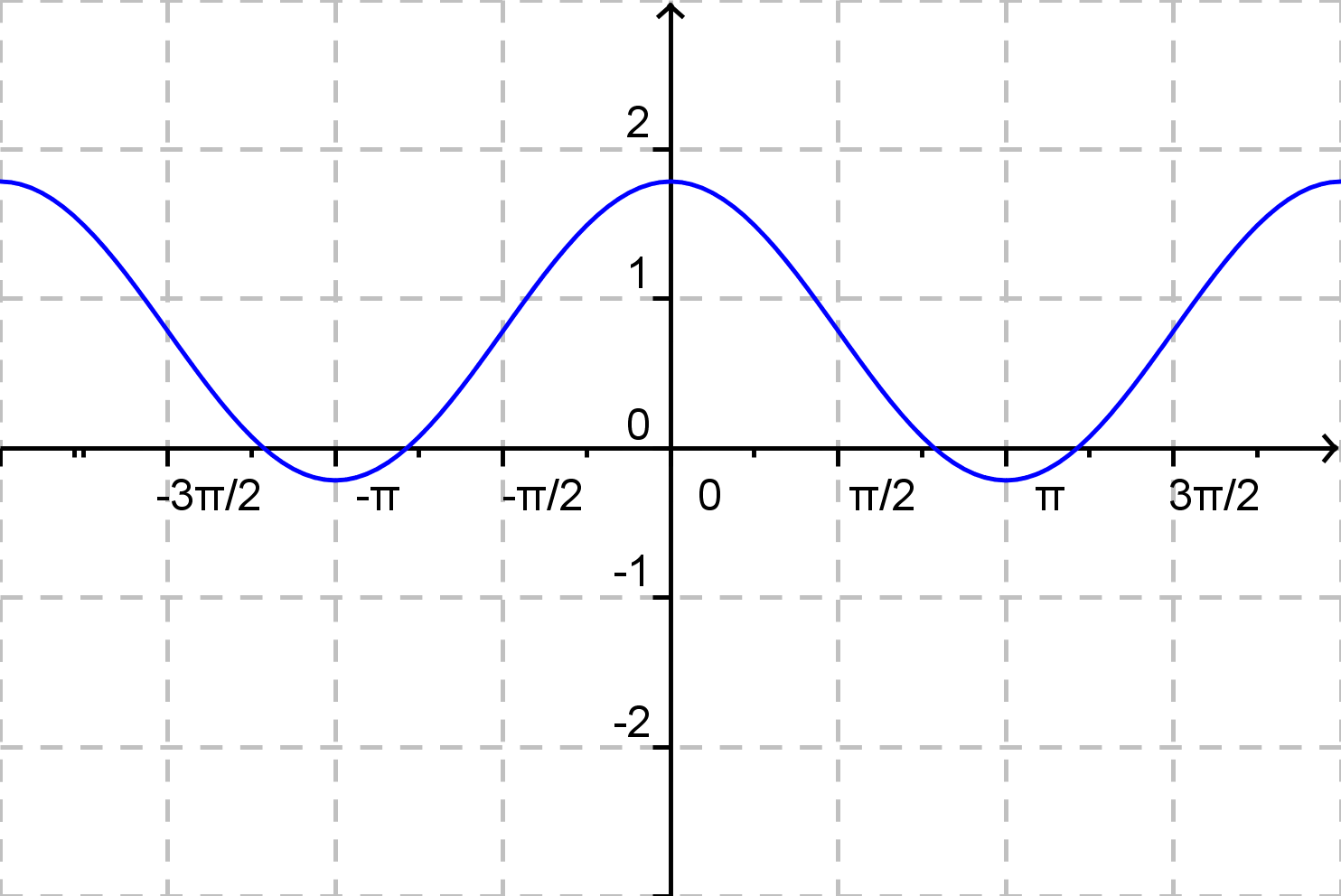
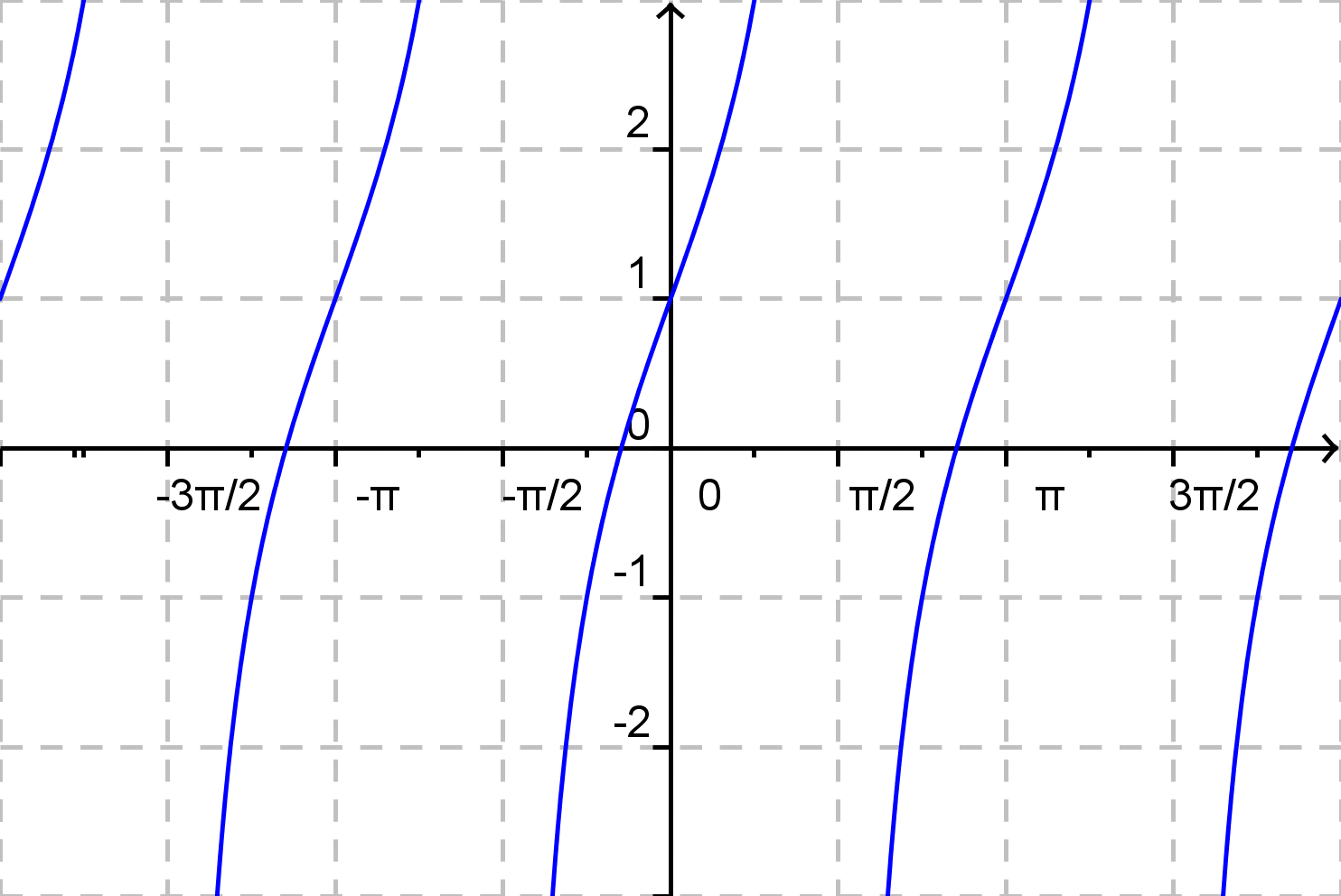
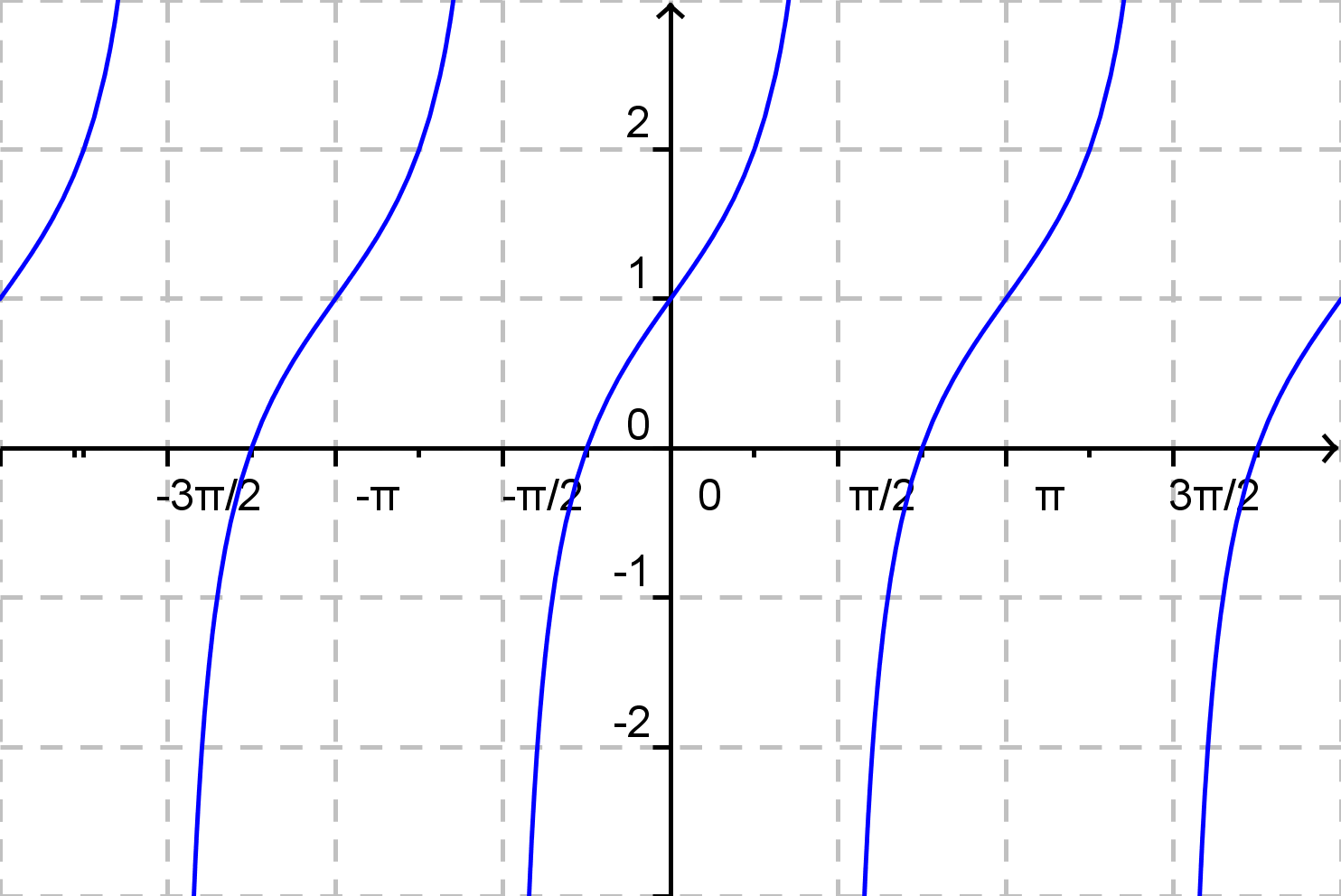
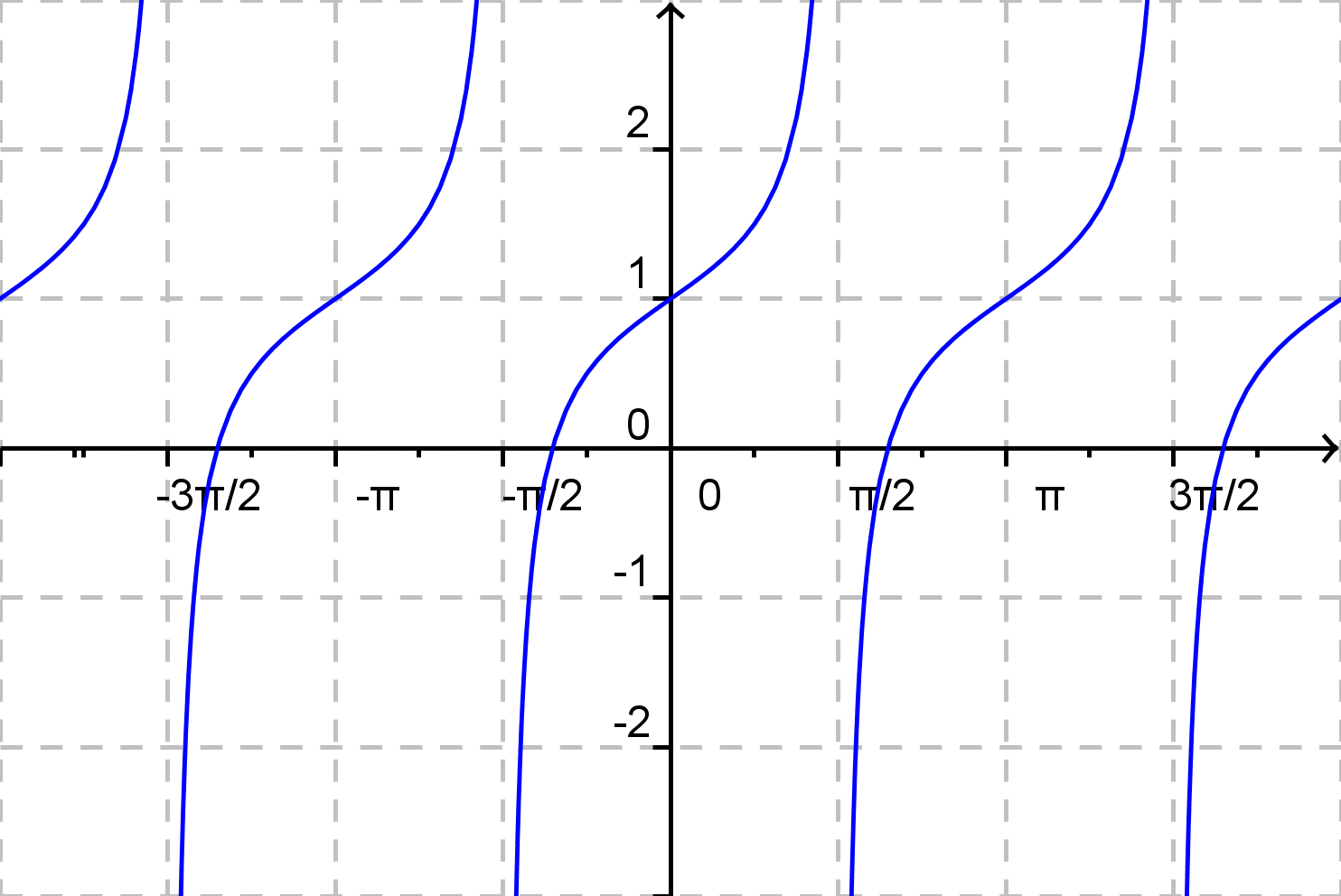
c)
\( f(x) = \frac {1}{2} {\rm tg}\: x + 1 \)
d)
\( f(x) = 2{\rm cotg}\: x -1 \)
