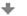Cyklometrické funkcie
Jedná sa o funkcie \(\arcsin x\) (čítame arkussínus), \(\arccos x\) (čítame arkuskosínus), \({\rm arctg}\: x\) (čítame arkustangens), \({\rm arccotg}\: x\) (čítame arkuskotangens), ktoré sú inverzné k funkciam goniometrickým.
Poznámka
Bližšie informácie o inverznej funkcií môžme nájsť v diplomovej práci Funkce.
Funkcie arkussínus a arkuskosínus
Definice
Inverzná funkcia k funkcii sínus, ktorá je definovaná na intervale \(<-\frac{\pi}{2}; \frac{\pi}{2}>,\) sa nazýva arkussínus, zapisujeme \(y = {\rm arcsin}\: x. \) Pričom platí \(x = \sin y,\) kde \(-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}.\)
Poznámka
Na iných intervalov, kde je \(x\) prostá, sa funkcia arkussínus nedefinuje.Definice
Inverzná funkcia k funkcii kosínus, ktorá je definovaná na intervale \(<0; \pi>,\) sa nazýva arkuskosínus, zapisujeme \(y = {\rm arccos}\: x. \) Pričom platí \(x = \cos y,\) kde \(0 \leq y \leq \pi.\)
Poznámka
Na iných intervalov, kde je \(x\) prostá, sa funkcia arkuskosínus nedefinuje.Základné vlastnosti cyklometrických funkcií arkussínus a arkuskosínus
V nasledujúcej tabuľke si môžme všimnuť vlastnosti goniometrických funkcií (s ohraničeným definičným oborom) a k nim inverzným cyklometrickým funkciam.
|
Funkcia |
\(\sin x\) |
\(\arcsin x\) |
\(\cos x\) |
\(\arccos x\) |
|
Definičný obor |
\(<-\frac {\pi}{2};\ \frac {\pi} {2}>\) |
\(<-1;\ 1>\) |
\(<0;\ \pi>\) |
\(<-1;\ 1>\) |
|
Obor funkčných hodnôt |
\(<-1;\ 1>\) |
\(<-\frac {\pi}{2};\ \frac {\pi} {2}>\) |
\(<-1;\ 1>\) |
\(<0;\ \pi>\) |
|
Monotónnosť |
funkcia je rastúca |
funkcia je rastúca |
funkcia je klesajúca |
funkcia je klesajúca |
Funkcie arkustangens a arkuskotangens
Definice
Inverzná funkcia k funkcii tangens, ktorá je definovaná pre každé \(x \in \mathbb{R},\) sa nazýva arkustangens, zapisujeme \(y = {\rm arctg}\: x. \) Pričom platí \(x = {\rm tg}\: y,\) kde \(-\frac{\pi}{2} < y < \frac{\pi}{2}.\)
Poznámka
Na iných intervalov, kde je \(x\) prostá, sa funkcia arkustangens nedefinuje.Definice
Inverzná funkcia k funkcii kotangens, ktorá je definovaná pre každé \(x \in \mathbb{R},\) sa nazýva arkuskotangens, zapisujeme \(y = {\rm arccotg}\: x. \) Pričom platí \(x = {\rm cotg}\: y,\) kde \(0 < y < \pi.\)
Poznámka
Na iných intervalov, kde je \(x\) prostá, sa funkcia arkuskotangens nedefinuje.Základné vlastnosti cyklometrických funkcií arkustangens a arkuskotangens
V nasledujúcej tabuľke si môžme všimnuť vlastnosti goniometrických funkcií (s ohraničeným definičným oborom) a k nim inverzným cyklometrickým funkciam.
|
Funkcia |
\({\rm tg}\: x\) |
\({\rm arctg}\: x\) |
\({\rm cotg}\: x\) |
\({\rm arccotg}\: x\) |
|
Definičný obor |
\((-\frac {\pi}{2};\ \frac {\pi} {2})\) |
\(\mathbb{R}\) |
\((0;\ \pi)\) |
\(\mathbb{R}\) |
|
Obor funkčných hodnôt |
\(\mathbb{R}\) |
\((-\frac {\pi}{2};\ \frac {\pi} {2})\) |
\(\mathbb{R}\) |
\((0;\ \pi)\) |
|
Monotónnosť |
funkcia je rastúca |
funkcia je rastúca |
funkcia je klesajúca |
funkcia je klesajúca |
Grafy cyklometrických a ďalších funkcií
Poznámka
Grafy cyklometrických funkcií sú vytvorené pomocou programu GeoGebra, kde sa používa iné značenie cyklometrických funkcií. Preto napríklad funkcia \({\rm arcsin}\: x\) sa v GeoGebre značí ako \({\rm asin}\: x.\)Arkussínus
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie arkus sínus.
Funkcia \(f(x)= a \cdot {\rm arcsin}\: (b\cdot x + c) + d.\)
Poznámka
Grafy cyklometrických funkcií sú zobrazované pomocou apletu. V jednotlivých apletoch je možné pomocou posuvníkov meniť základné hodnoty parametrov \(a,b,c,d.\) Je dôležité si všímať práve tieto zmeny a uvedomiť si, ako vplýva každý parameter na danú funkciu.
Arkuskosínus
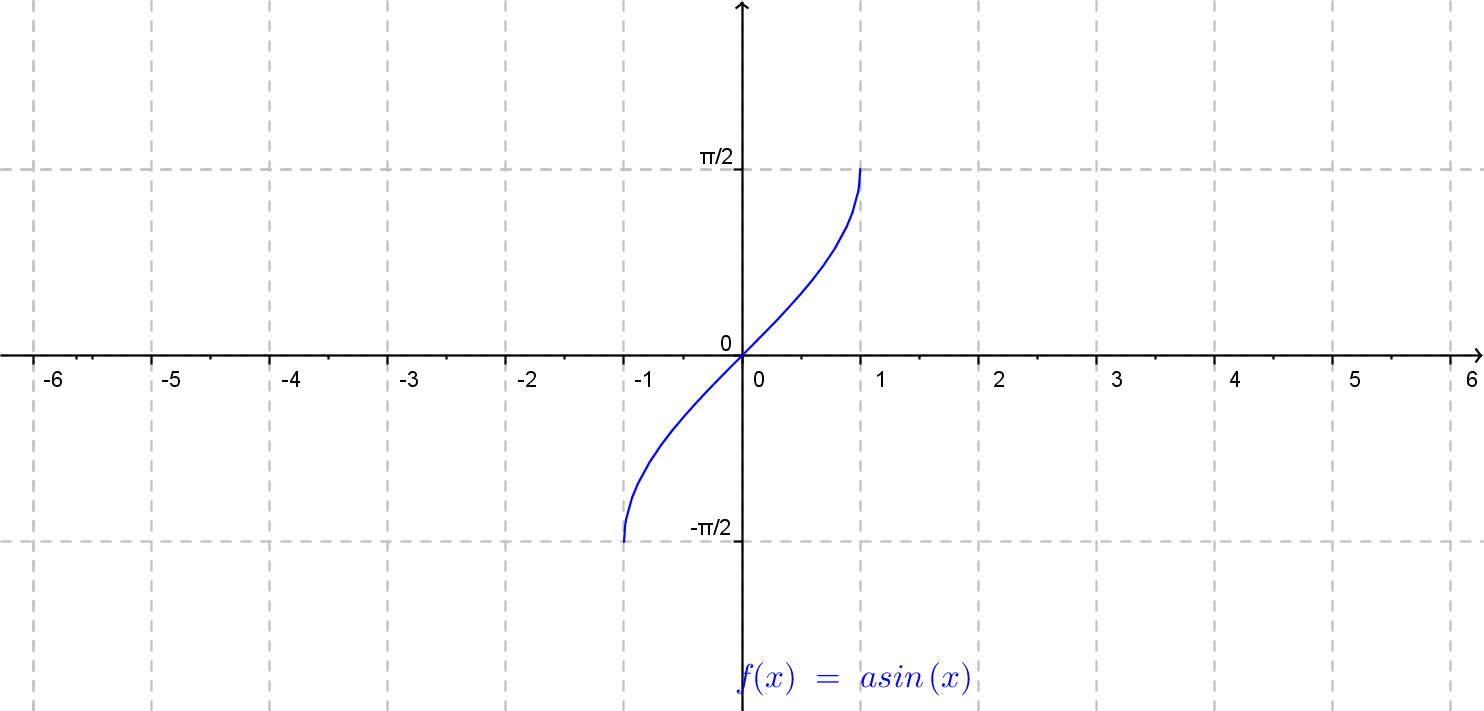
V nasledujúcom obrázku sa môźme pozrieť na obecný graf funkcie arkuskosínus.
Funkcia \(f(x)= a \cdot {\rm arccos}\: (b\cdot x + c) + d.\)
Arkustangens
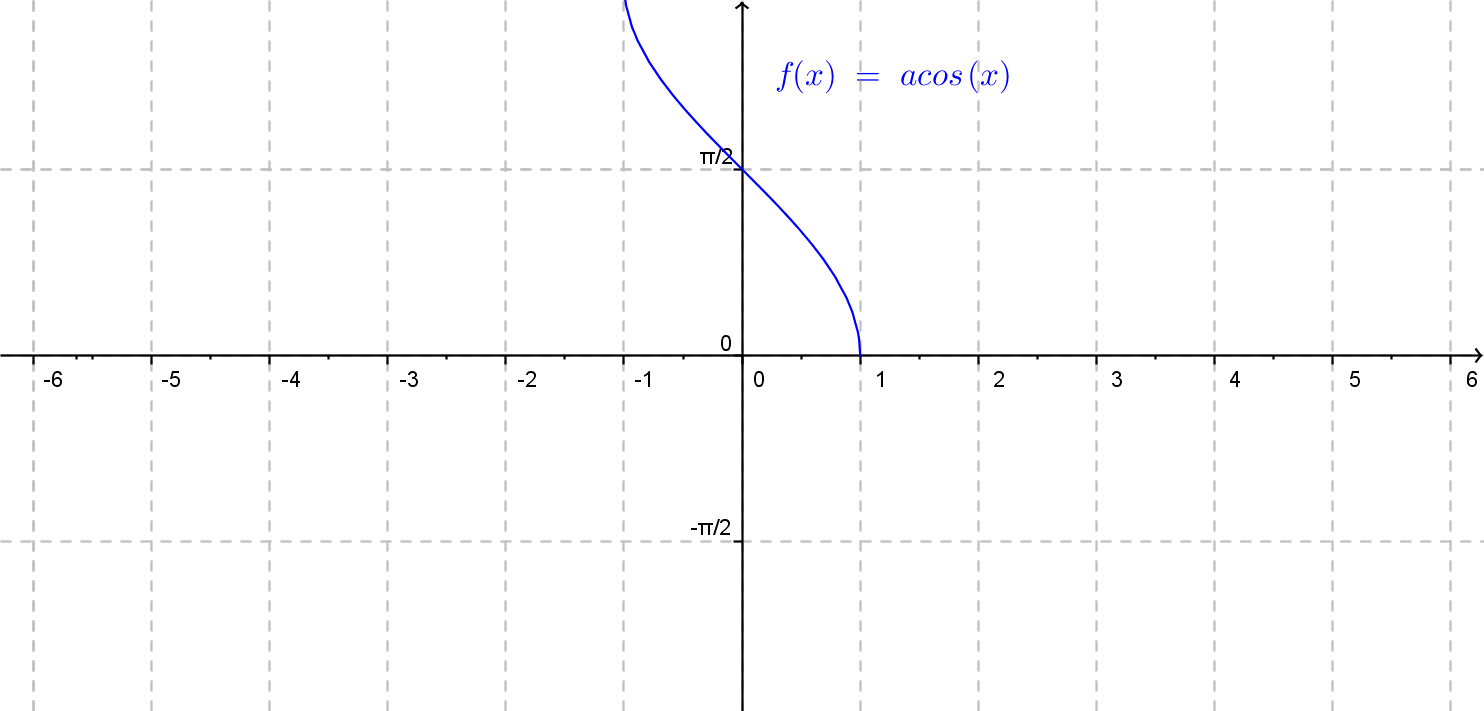
Obecný graf funkcie arkustangens je znázornený na nasledujúcom obrázku.
Funkcia \(f(x)= a \cdot {\rm arctg}\: (b\cdot x + c) + d.\)
Arkuskotangens
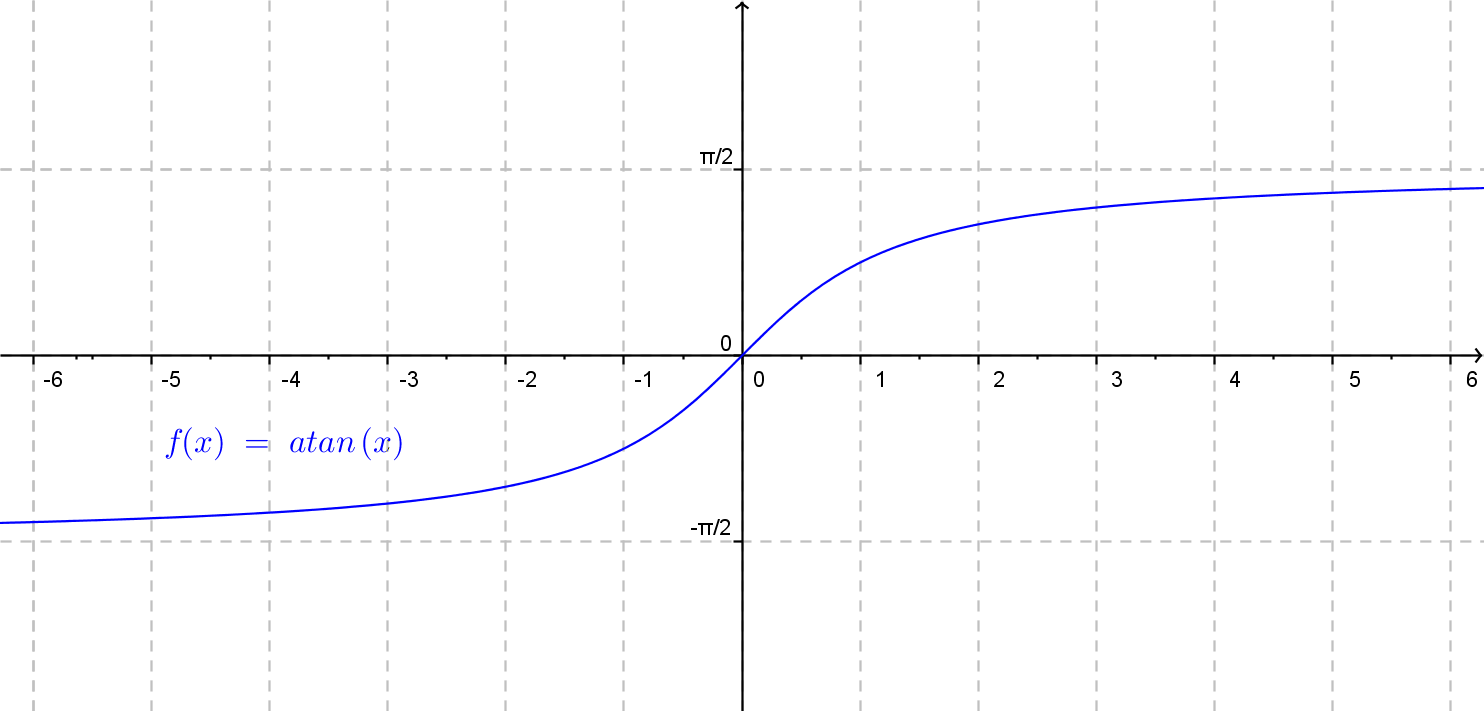
Obecný graf funkcie arkuskotangens je znázornený na nasledujúcom obrázku.
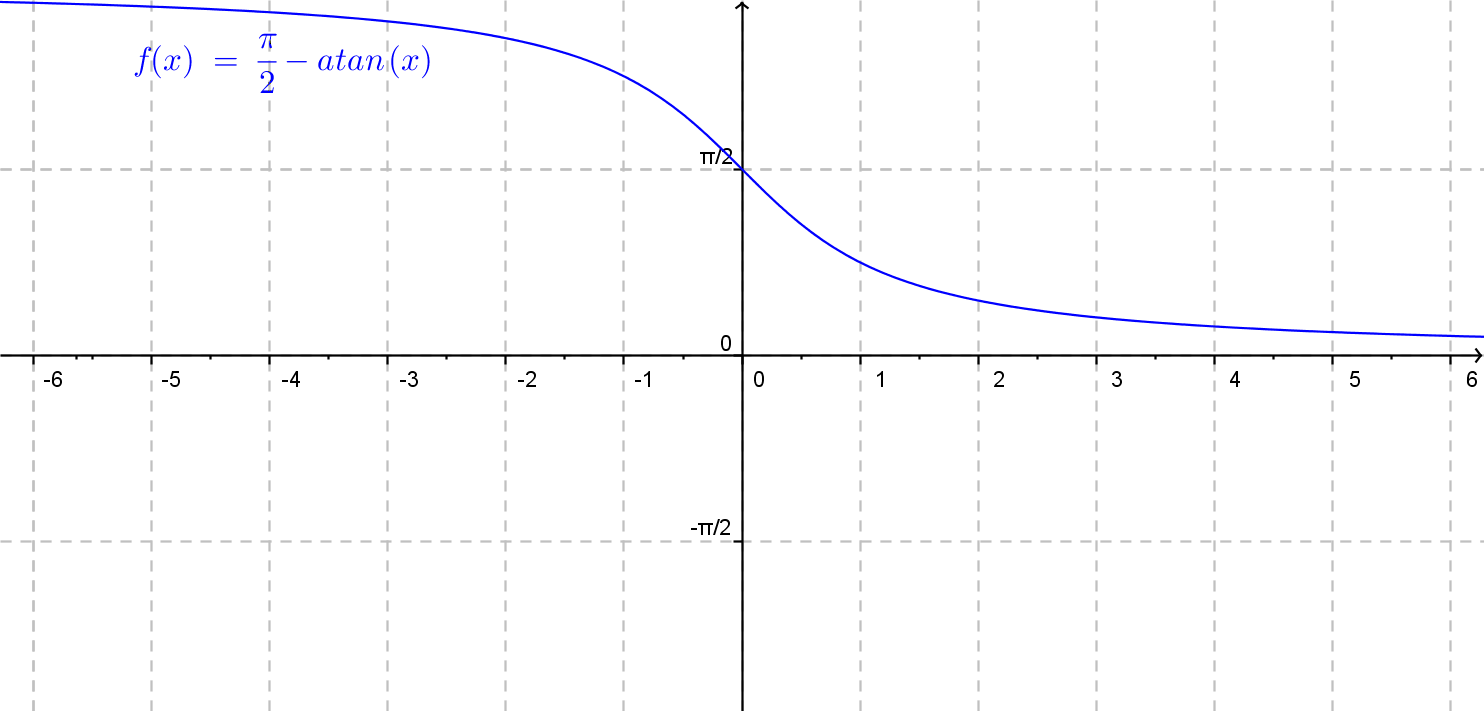
Funkcia \(f(x)= a \cdot {\rm arccotg}\: (b\cdot x + c) + d.\)
Veta
Pre cyklometrické funkcie platí:
\(\arcsin 0 = 0,\quad \arcsin \frac {1}{2} = \frac {\pi}{6},\quad \arcsin 1 = \frac {\pi}{2},\quad \arcsin (-1) = -\frac {\pi}{2};\)\(\arccos 0 = \frac{\pi}{2},\quad \arccos \frac {1}{2} = \frac {\pi}{3},\quad \arccos 1 = 0,\quad \arccos (-1) = \pi;\)
\(\rm arctg\ 0 = 0,\quad \rm arctg\ 1 = \frac {\pi}{4};\)
\(\rm arccotg\ 0 = \frac{\pi}{2},\quad \) \(\rm arccotg\ 1 = \frac{\pi}{4}.\)Poznámka
Dôkaz tejto vety je trivialny, vychádza z vlastnosti inverzných funkcií. Napríklad \(\arcsin 1 = \frac {\pi}{2},\) lebo \(\sin \frac {\pi}{2} = 1.\) Podobne postupujeme v ostatných prípadoch.