Cvičení 12 - Optimalizace a další užitečné funkce
Jan Vávra
Rkový skript ke stažení: R
Co si zde představíme?
- funkci
optimizepro funkci jedné proměnné, - všeobecnou funkci
optimpro nalezení extrému funkce, - derivování a integrování pomocí Rka.
Funkce optimize
Funkce o jedné proměnné lze numericky optimalizovat pomocí funkce
optimize. Více o metodě hledání optima se lze dočíst v
helpu ?optimize. Kromě zadané funkce ještě potřebuje
interval, na kterém má hledat. Bohužel neakceptuje celou reálnou přímku,
tedy c(-Inf, Inf). Argumentem maximum můžete
přesnit, zda se má maximalizovat či minimalizovat. Také si můžete
opohrát s tolerancí přesnosti řešení.
f1 <- function(x){x^2+1}
(o1 <- optimize(f1, interval = c(-10e9, 10e9))) # defaultní nastavení minimalizuje## $minimum
## [1] 0
##
## $objective
## [1] 1Výsledkem je list o dvou hodnotách - bod extrému minimum
a dosažená min/max hodnota funkce objective.
Někdy máte funkci o více parametrech, ale chcete optimalizovat jen v
jednom z parametrů. Hodnoty ostatních fixních parametrů lze udat jako
další argumenty funkce optimize:
f2 <- function(x, a, b, c){a * x^2 + b * x + c}
(o2 <- optimize(f2, interval = c(-10e9, 10e9),
a = -1, b = 2, c = 0, # upřesnění ostatních parametrů funkce f2
maximum = TRUE)) # budeme maximalizovat## $maximum
## [1] 0.9999995
##
## $objective
## [1] 1Co se stane, pokud má funkce nějaká lokální minima? Metoda zlatého řezu, kterou funkce používá, má svá “slepá” místa:
f3 <- function(x){2*sin(x) + 0.5*cos(x) + x}
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
curve(f3, from = -10, to = 10, col = "blue", lwd = 2)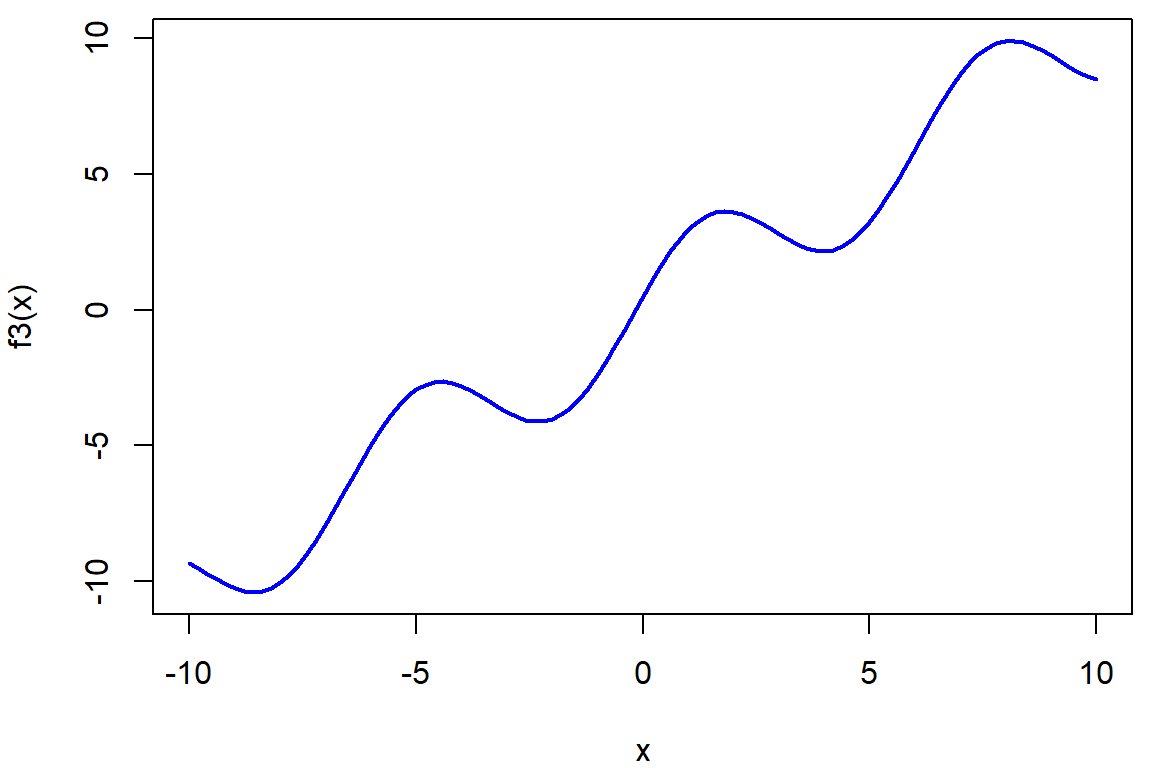
optimize(f3, interval = c(-10, 10)) # ne, podle obrázku to globálnímu minimu neodpovídá## $minimum
## [1] -2.322206
##
## $objective
## [1] -4.124995.Machine$double.eps^0.25 # nastavená defaultní tolerance## [1] 0.0001220703optimize(f3, interval = c(-10, 10), tol = .Machine$double.eps) # ani snížení tolerance nepomáhá## $minimum
## [1] -2.32222
##
## $objective
## [1] -4.124995optimize(f3, interval = c(-10, 10), maximum = TRUE) # to víceméně sedí ## $maximum
## [1] 8.115454
##
## $objective
## [1] 9.918223f4 <- function(x){-f3(x)}
optimize(f4, interval = c(-10, 10), maximum = TRUE) # nepomohlo## $maximum
## [1] -2.322206
##
## $objective
## [1] 4.124995# A co si zkusit dodefinovat funkci f3 na krajích konstantně?
f5 <- function(x){
newx <- pmin(x, 10)
newx <- pmax(newx, -10)
return(f3(newx))
}
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
curve(f5, from = -20, to = 20, col = "blue", lwd = 2)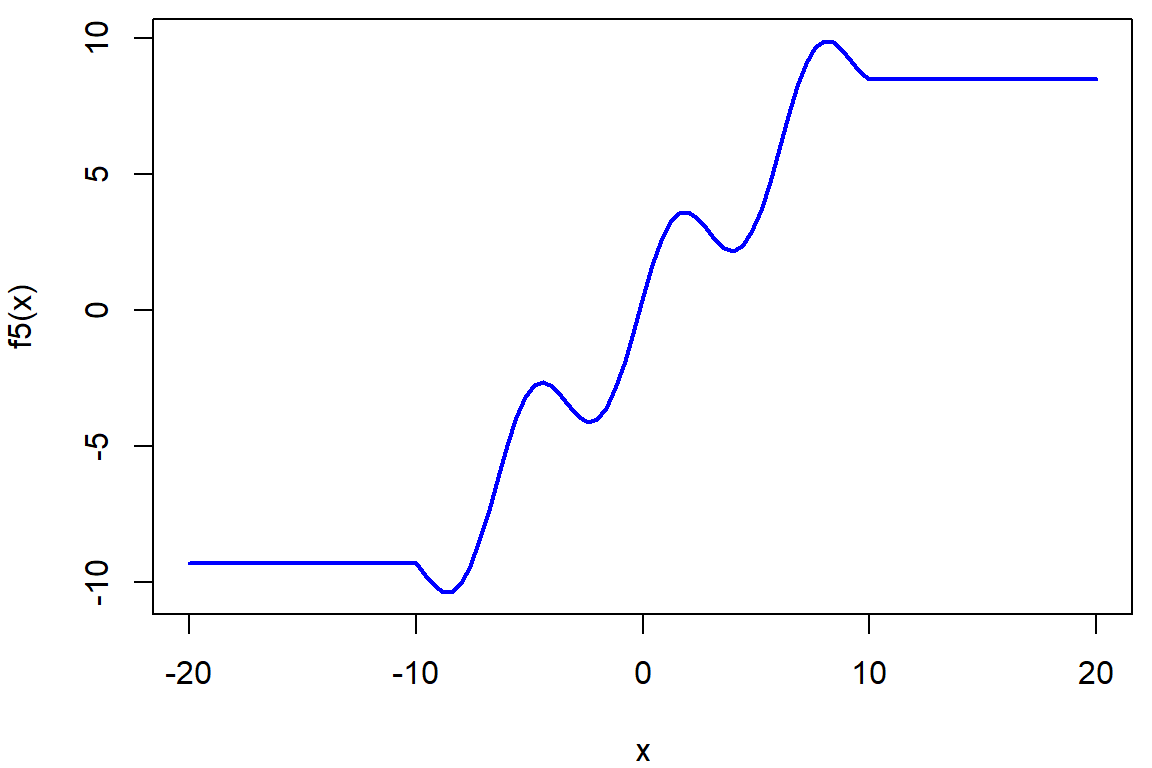
optimize(f5, interval = c(-20, 10)) # změna intervalu pomohla## $minimum
## [1] -8.605422
##
## $objective
## [1] -10.40818# ?optimize # zde je "vysvětlení"Co když jsou optima na krajích intervalu?
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
curve(f3, from = -8, to = 8, col = "blue", lwd = 2)
optimize(f3, interval = c(-8, 8)) # opět nachází lokální minimum## $minimum
## [1] -2.322221
##
## $objective
## [1] -4.124995optimize(f3, interval = c(-8, 8), maximum = TRUE) # taky jen lokální maximum## $maximum
## [1] 1.832275
##
## $objective
## [1] 3.635038# Zkusme opět dodefinování konstantou na krajích
f6 <- function(x){
newx <- pmin(x, 8)
newx <- pmax(newx, -8)
return(f3(newx))
}
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
curve(f6, from = -20, to = 20, col = "blue", lwd = 2)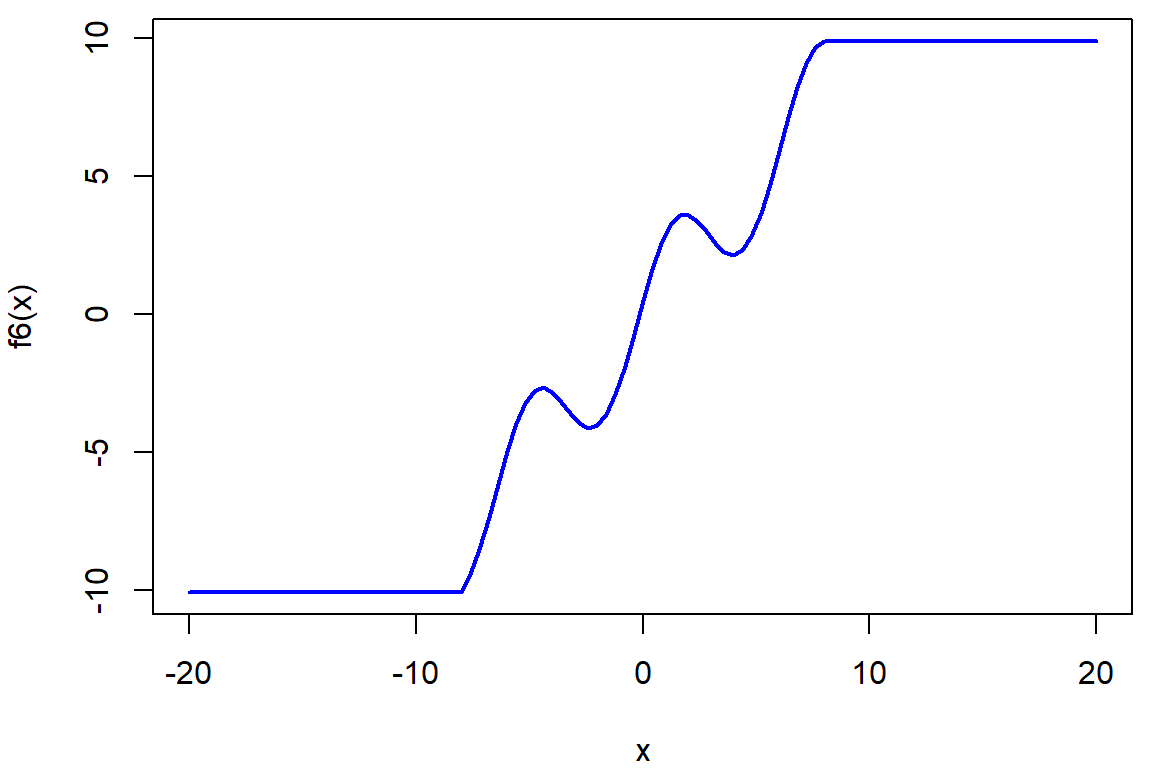
optimize(f6, interval = c(-20, 20)) # změna intervalu pomohla, ale mimo[-8, 8]## $minimum
## [1] -14.164
##
## $objective
## [1] -10.05147optimize(f6, interval = c(-20, 20), maximum = T) # je třeba výsledek oseknout zpátky do [-8, 8]## $maximum
## [1] 10.55735
##
## $objective
## [1] 9.905966S funkcí optimize ještě úzce souvisí funkce
uniroot na hledání kořenů funkce, tj. \(f(x) = 0\) pro \(x\) ve vymezeném intervalu. Má ale svá
omezení, například na koncích intervalů se očekává, že má opačná
znaménka:
# uniroot(f2, c(-10, 10), a = -1, b = 2, c = 0) # vrací error
uniroot(f2, c(-10, 1), a = -1, b = 2, c = 0) # téměř 0## $root
## [1] 3.605162e-06
##
## $f.root
## [1] 7.210312e-06
##
## $iter
## [1] 12
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05uniroot(f2, c(1, 10), a = -1, b = 2, c = 0) # téměř 2## $root
## [1] 1.999998
##
## $f.root
## [1] 3.054496e-06
##
## $iter
## [1] 11
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05# A co když znaménka na krajích intervalů jsou opačná, ale kořenů je víc?
f7 <- function(x){2*sin(x) + 0.5*cos(x) + x - 3}
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
curve(f7, from = 1, to = 5, col = "blue", lwd = 2)
abline(h = 0, col = "grey", lty = 2)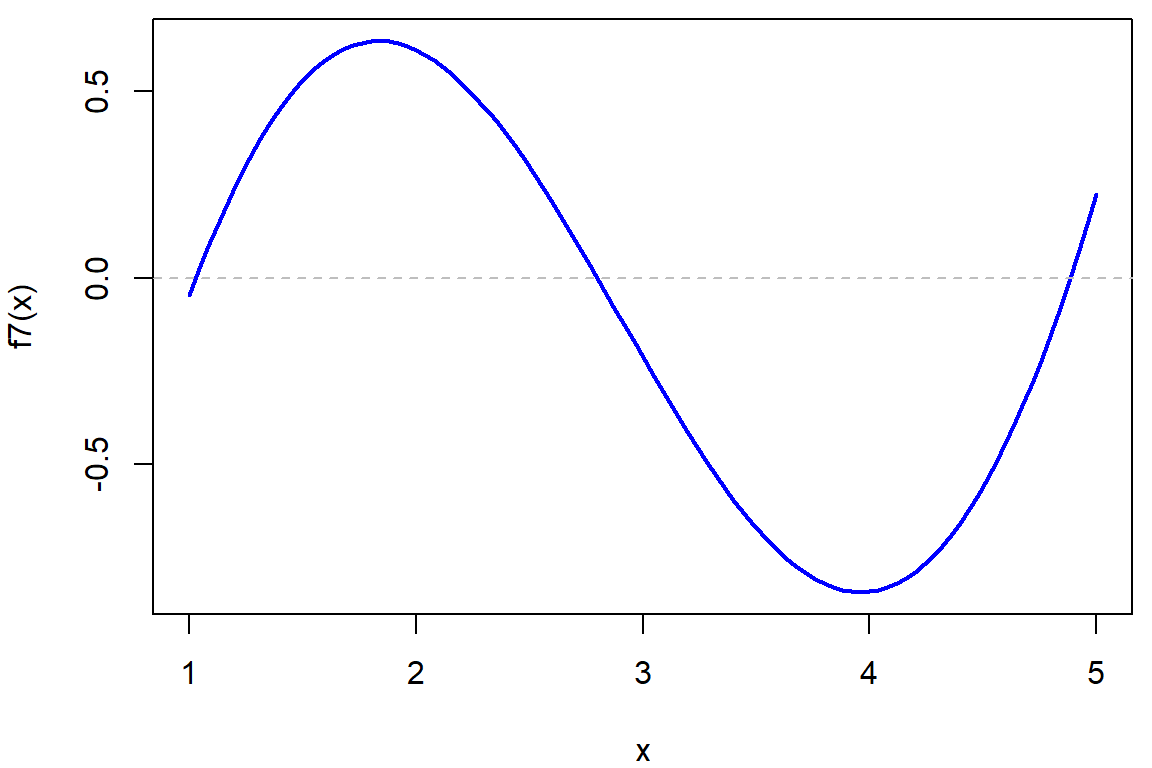
uniroot(f7, interval = c(1,5)) # stále nachází jen jediný ## $root
## [1] 1.028747
##
## $f.root
## [1] -2.67886e-07
##
## $iter
## [1] 5
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05# Musíme si rozložít na vícero podintervalů (což bychom tedy bez grafu asi těžko uhodli...)
uniroot(f7, interval = c(1,2)) ## $root
## [1] 1.02876
##
## $f.root
## [1] 2.111734e-05
##
## $iter
## [1] 4
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05uniroot(f7, interval = c(2,4))## $root
## [1] 2.798926
##
## $f.root
## [1] -5.552229e-06
##
## $iter
## [1] 4
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05uniroot(f7, interval = c(4,5))## $root
## [1] 4.884649
##
## $f.root
## [1] -4.520939e-05
##
## $iter
## [1] 4
##
## $init.it
## [1] NA
##
## $estim.prec
## [1] 6.103516e-05Ještě je možnost použít funkci uniroot.all z balíčku
rootSolve, která najde kořeny všechny:
library("rootSolve")
uniroot.all(f7, interval = c(1,5))## [1] 1.028573 2.798917 4.884591Pro polynomiální problémy, tedy \(f(x) =
0\), kde \(f\) je polynom
libovolného řádu, má Rko funkci polyroot. Problém však je,
že vrací komplexní čísla místo reálných.
(x <- polyroot(c(1, 2, 1))) # x^2 + 2x + 1 = 0, vrací i komplexní čísla## [1] -1-1.110223e-16i -1+1.110223e-16iclass(x) # třída pro komplexní čísla... doposud jsem nepotřeboval## [1] "complex"Re(x) # reálná část## [1] -1 -1Im(x) # imaginární část## [1] -1.110223e-16 1.110223e-16Mod(x) # modulus = absolutní hodnota (vzdálenost od [0+0i])## [1] 1 1Arg(x) # argument = úhel pro geometrický tvar komplexního čísla## [1] -3.141593 3.141593Conj(x) # konjugované komplexní číslo## [1] -1+1.110223e-16i -1-1.110223e-16ipolyroot(c(1,-2,1)) # i když čistě reálná řešení existují, stejně komplexní## [1] 1+5.551115e-17i 1-5.551115e-17iRe(polyroot(c(1,-2,1))) # takto by to asi šlo, ale musíme vědět, že budou reálná## [1] 1 1Funkce optim
Tato funkce již umí optimalizovat funkci více parametrů. Ovšem zápis je poněkud komplikovanější, třeba kvůli tomu, že parametry musí být v jednom vektoru. Dále také proto, že optimalizačních metod je na výběr více. Je také zapotřebí dodat výchozí hodnoty, kde má algoritmus startovat.
f8 <- function(x){(x[1]-pi)^2 + (x[2]-exp(1))^2 + 1}
optim(par = list(x = 0, y = 0), f8) # method = Nelder-Mead, lower = -Inf, upper = Inf## $par
## x y
## 3.14122 2.71827
##
## $value
## [1] 1
##
## $counts
## function gradient
## 75 NA
##
## $convergence
## [1] 0
##
## $message
## NULLNastavení výchozích hodnot je možná “otravná práce”, ale při složitějších problémech, kde hrozí lokální minima, se osvědčuje nastartovat algoritmus ze spousty různých hodnot
f9xy <- function(x,y){sin(x)*cos(y) + x*y / 20}
f9 <- function(x){sin(x[1])*cos(x[2]) + x[1]*x[2] / 20}
optim(par = list(x = 0, y = 0), function(x){sin(x[1])*cos(x[2]) + x[1]*x[2]}) # diverguje## $par
## x y
## -3.183805e+55 2.684172e+55
##
## $value
## [1] -8.545879e+110
##
## $counts
## function gradient
## 501 NA
##
## $convergence
## [1] 1
##
## $message
## NULLoptim(par = list(x = 0, y = 0), f9) # lokální minimum## $par
## x y
## -1.57474962 0.07881972
##
## $value
## [1] -1.003094
##
## $counts
## function gradient
## 119 NA
##
## $convergence
## [1] 0
##
## $message
## NULL# Nyní s omezením na interval [-2pi,2pi]^2 s výchozími hodnotami (0,0) - třeba změnit metodu na L-BFGS-B
optim(par = c(0, 0), f9, lower = rep(-2*pi,2), upper = rep(2*pi,2), method = "L-BFGS-B") # lokání minimum## $par
## [1] -1.57475008 0.07881986
##
## $value
## [1] -1.003094
##
## $counts
## function gradient
## 7 7
##
## $convergence
## [1] 0
##
## $message
## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"# Při jiných výchozích hodnotách dojdeme k jinému minimu
optim(par = c(4, -4), f9, lower = rep(-2*pi,2), upper = rep(2*pi,2), method = "L-BFGS-B") # na hranici## $par
## [1] 5.031960 -6.283185
##
## $value
## [1] -2.530207
##
## $counts
## function gradient
## 9 9
##
## $convergence
## [1] 0
##
## $message
## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"# Algoritmu lze pomoci dodáním gradientové funkce
gf9 <- function(x){ # gradientová funkce
c(cos(x[1])*cos(x[2]) + x[2]/20,
-sin(x[1])*sin(x[2]) + x[1]/20)
}
optim(par = c(0,0), f9, gr = gf9, lower = rep(-2*pi,2), upper = rep(2*pi,2), method = "L-BFGS-B")## $par
## [1] -1.57475008 0.07881985
##
## $value
## [1] -1.003094
##
## $counts
## function gradient
## 7 7
##
## $convergence
## [1] 0
##
## $message
## [1] "CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH"# Ovšem ani to nenalezlo opravdové optimum (dle obrázku)
# Jednoduše lze použít pro více startovních hodnot naráz - matice N×2 (počet sloupců = počet proměnných)
start <- matrix(rnorm(2*15, sd = 2), ncol = 2) # náhodné výchozí body
optimf9 <- apply(start, 1,
function(par, ...){o <- optim(par, ...); return(c(o$par, o$value))},
f9, lower = rep(-2*pi,2), upper = rep(2*pi,2), method = "L-BFGS-B")
(pars <- t(optimf9[1:2,]))## [,1] [,2]
## [1,] 1.733619 -3.22954883
## [2,] 1.733619 -3.22954883
## [3,] 1.416293 3.06986308
## [4,] -1.574750 0.07881955
## [5,] -1.253987 -6.21715426
## [6,] -1.890367 6.28318531
## [7,] 1.416293 3.06986274
## [8,] 5.031960 -6.28318531
## [9,] -1.574750 0.07881969
## [10,] 4.724662 -0.23850574
## [11,] -1.574751 0.07882031
## [12,] 1.416293 3.06986277
## [13,] -1.574750 0.07881946
## [14,] -1.890367 6.28318531
## [15,] -1.574750 0.07881951(vals <- optimf9[3,])## [1] -1.2628995 -1.2628995 -0.7681560 -1.0030936 -0.5583519 -1.5432467 -0.7681560 -2.5302071 -1.0030936
## [10] -1.0279618 -1.0030936 -0.7681560 -1.0030936 -1.5432467 -1.0030936which.min(vals)## [1] 8# Sice jsme tentokrát minimum našli, ale příště to štěstí mít nemusíme, stále může být jen lokální!
# Zakreslíme si to do obrázku, abychom se o tom přesvědčili.
y <- x <- seq(-2*pi, 2*pi, length.out = 201) # x-ové a y-ové hodnoty
z <- outer(x, y, FUN = f9xy) # z = sin(x) * cos(y) + x * y / 20, každý s každým
rz <- range(z)
barev <- 100
breaks <- seq(rz[1], rz[2], length.out = barev+1)
COLs <- hcl.colors(barev, palette = "YlGnBu")
layout(matrix(c(1,2), nrow = 1, byrow = TRUE), # dva obrázky vedle sebe
widths=c(5,1)) # šířkově v poměru 5:1 (druhý bude velmi hubený)
par(mar = c(4,4,2.5,0.5))
# barevné vykreslení hodnot funkce o dvou proměnných (heatmap)
image(x, y, z, main = c("f(x,y) = sin(x) * cos(y) + x*y/20"), bty = "n",
breaks = breaks, col = COLs, # kategorizace hodnot + barevné schéma
asp = 1) # zachová poměr x a y os 1:1
# zakreslení optimálního bodu
points(start, col = "palevioletred", pch = 16, cex = 0.5) # výchozí pozice
arrows(x0 = start[,1], x1 = pars[,1], # šipka směrem od startu
y0 = start[,2], y1 = pars[,2], col = "violetred", length = 0.1) # k lokálnímu minimu
points(pars, col = "orange", pch = 16, cex = 1) # lokální minima
points(pars[which.min(vals), , drop = F], col = "red", pch = 8, cex = 1.5) # globální
# legenda jako separátní obrázek
par(mar = c(4,0,2.5,3)) # horní a dolní okraje stejné, žádný vlevo, napravo delší
plot(0, 0, type ="n", # bty = "n", # NIC nekreslit, jen otevřít kreslící okno
xlim = c(0,1), ylim = rz, # rozsah y hodnot odpovídající hodnotám funkce
xaxs = "i", yaxs = "i", # žádné vnitřní rozšíření xlim a ylim hodnot
xaxt = "n", yaxt = "n", # bez os x a y
xlab = "", ylab = "") # žádné popisky os
axis(4, pretty(breaks), las = 2) # vlastní osa napravo
rect(xleft = 0, xright = 1, # obdélníky po celé šíři vykreslovací plochy
ybottom = breaks[-length(breaks)], # dolní hodnoty úzkých obdélníků
ytop = breaks[-1], # horní hodnoty úzkých obdélníků
col = COLs, border = NA) # barevné vyplnění obdélníků bez ohraničení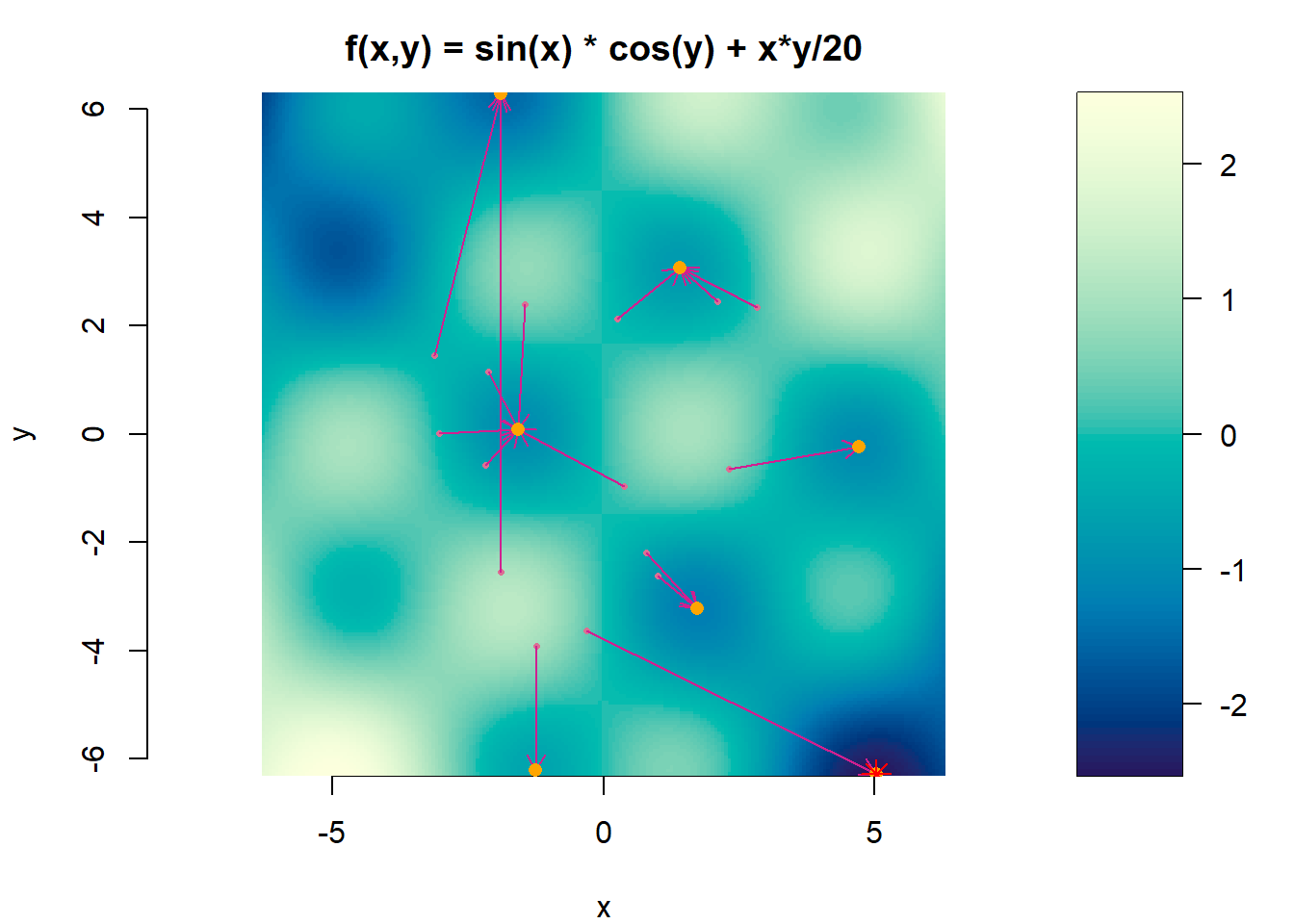
Další příklady použití funkce optim lze nalézt v helpu
?optim. Je tam navržen postup jak postupovat v případě
velmi divoké funkce nejprve metoda SANN a výsledek použít
jako výchozí bod pro další metodu pro upřesnění. Nebo je tam také
ukázáno, jak se pomocí optim dá řešit problém
obchodního cestujícího.
Další funkce - derivování a integrování
Derivování funkcí pomocí Rka je také možné. Jen to není tolik
intuitivní. Gradient funkce se vrací jako atribut při použití funkce
deriv. Při vyhodnocení původní funkce se tak dozvíme i
hodnoty gradientu.
x <- seq(-5,5, length.out = 11); a = 1; b = 2; c = pi
f2 <- deriv(~a * x^2 + b * x + c, "x") # výstupem je opět stejná funkce, ale gradient jako atribut
f2dash <- eval(f2) # bere si argumenty z existujících proměnných x, a, b, c
f2dash # hodnoty funkce## [1] 18.141593 11.141593 6.141593 3.141593 2.141593 3.141593 6.141593 11.141593 18.141593 27.141593
## [11] 38.141593
## attr(,"gradient")
## x
## [1,] -8
## [2,] -6
## [3,] -4
## [4,] -2
## [5,] 0
## [6,] 2
## [7,] 4
## [8,] 6
## [9,] 8
## [10,] 10
## [11,] 12attr(f2dash, "gradient") # hodnoty gradientu jako atribut## x
## [1,] -8
## [2,] -6
## [3,] -4
## [4,] -2
## [5,] 0
## [6,] 2
## [7,] 4
## [8,] 6
## [9,] 8
## [10,] 10
## [11,] 12f3 <- deriv(~2*sin(x) + 0.5*cos(x) + x, "x", function.arg = TRUE) # takto se bude chovat jako funkce
f3(x)## [1] -2.940320 -2.813217 -3.777236 -4.026668 -2.412791 0.500000 2.953093 3.610521 2.787244 2.159573
## [11] 3.223983
## attr(,"gradient")
## x
## [1,] 1.08786223
## [2,] -0.68568849
## [3,] -0.90942499
## [4,] 0.62235504
## [5,] 2.50134010
## [6,] 3.00000000
## [7,] 1.65986912
## [8,] -0.28694239
## [9,] -1.05054500
## [10,] 0.07111401
## [11,] 2.04678651unif <- uniroot(f3, interval = c(-5, 5)) # lze použít k hledání kořene f3, navíc vrátí i gradient
f3(unif$root) # skoro nulová hodnota funkce (derivace 3, rostoucí na okolí)## [1] 3.309406e-06
## attr(,"gradient")
## x
## [1,] 3.054947unif$f.root## [1] 3.309406e-06
## attr(,"gradient")
## x
## [1,] 3.054947optif <- optimize(f3, interval = c(-5,5))
attr(optif$objective, "gradient") # gradient skoro nulový## x
## [1,] 2.209308e-06# Funkce více proměnných
y <- -5:5
f9 <- deriv(~sin(x)*cos(y) + x*y / 20, c("x", "y"), function.arg = TRUE)
f9(x,y)## [1] 1.5220106 0.3053209 0.5897077 0.5784012 -0.4046487 0.0000000 0.5046487 -0.1784012 0.3102923
## [10] 1.2946791 0.9779894
## attr(,"gradient")
## x y
## [1,] -0.16953576 -1.1695358
## [2,] 0.22724998 -0.7727500
## [3,] 0.83008514 -0.1699149
## [4,] 0.07317819 -0.9268218
## [5,] 0.24192658 -0.7580734
## [6,] 1.00000000 0.0000000
## [7,] 0.34192658 -0.6580734
## [8,] 0.27317819 -0.7268218
## [9,] 1.13008514 0.1300851
## [10,] 0.62724998 -0.3727500
## [11,] 0.33046424 -0.6695358Opačný proces, integrování, je daleko přímočařejší, tedy aspoň pro
určitý integrál funkce jedné proměnné. Z jiných předmětů víme, jak se
integrál dá numericky aproximovat rozdělením na menší podintervaly. V
Rku pro výpočet máme funkci integrate, přičemž detaily o
její implementaci jsou v helpu ?integrate:
(Sf3 <- integrate(f3, lower = -3, upper = 5))## 5.043789 with absolute error < 2.4e-13(Sf3plus <- integrate(f3, lower = unif$root, upper = 5))## 13.49456 with absolute error < 1.5e-13(Sf3minus <- integrate(f3, lower = -3, upper = unif$root))## -8.450775 with absolute error < 9.4e-14hodnoty <- c(Sf3$value, Sf3plus$value, Sf3minus$value)
hezky <- format(hodnoty, digits = 3, nsmall = 2)
par(mfrow = c(1,1), mar = c(4,4,0.5,0.5))
curve(f3, from = -4, to = 6, col = "black", lwd = 1)
abline(h = 0, col = "darkslategrey", lty = 2)
abline(v = c(-3,5), col = "darkslategrey", lty = 2)
x <- seq(unif$root, 5, length.out = 101)
polygon(c(x, 5), c(f3(x), 0), col = "skyblue", border = "darkblue", lwd = 2, lty = 1)
text(2, 1, hezky[2], cex = 2, font = 2)
x <- seq(-3, unif$root, length.out = 101)
polygon(c(-3, x), c(0, f3(x)), col = "tan", border = "orangered", lwd = 2, lty = 1)
text(-2, -1, hezky[3], cex = 2, font = 2)
text(1, 5, paste0(hezky[1], " = ", hezky[2], " - ", sub("-","",hezky[3])), cex = 2, font = 2)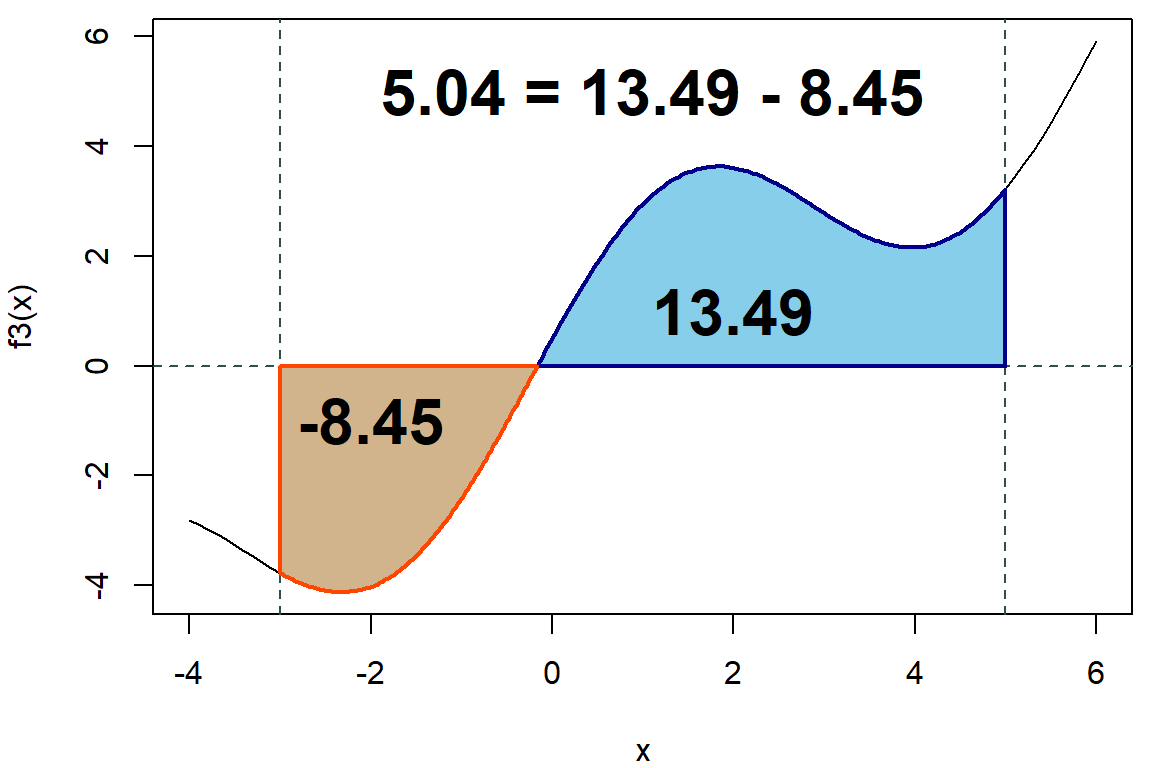
Úložky na procvičení
Vyřešte si to sami, aniž byste se dívali do řešení (úplně dole vespod skriptu).
Autoregresní posloupnost. Nagenerujte si posloupnost čísel
ytak, že nová hodnota je \(\phi=0.9\)-násobek hodnoty předchozí, ke které je přidán náhodný šum (centrované normální rozdělení). Následně se pokuste metodou alá nejmenší čtverce nalézt nejvhodnější \(\phi\), tedy takovou hodnotu, která minimalizuje \(\sum\limits_{i=2}^n (y_i - \phi y_{i-1})^2\). Stacionarita procesu je zajištěna, pokud \(|\phi| < 1\), omezte tedy optimalizaci. Porovnejte nalezenou hodnotu se skutečnou hodnotou, kterou jste použili ke generování.Pro množinu bodů v rovině, vyřešte úlohu nejmenších čtverců pomocí funkce
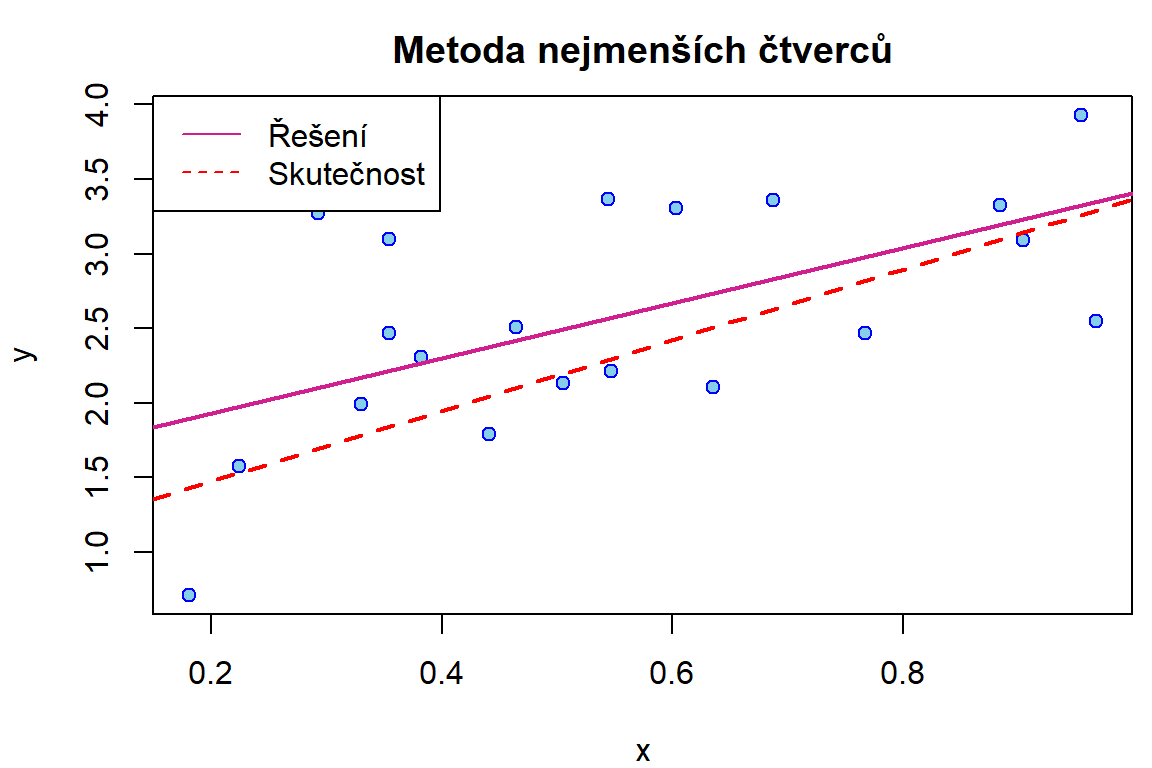
optim. Tedy máme dané páry hodnot \(\mathbf{x}\) a \(\mathbf{y}\) a chceme nalézt \(\beta_1\) a \(\beta_2\) tak, aby byl minimalizován součet čtverců \(\sum\limits_{i=1}^{n}(y_i - (\beta_1 + \beta_2 x_i))^2\). Body si vygenerujte náhodně a zaveďte si nějakou závislost. Výslednou přímku zakreslete do grafu.
Pozn.: víme, že řešení lze nalézt efektivně a explicitně, např.
pomocí QR rozkladu. V Rku to provádí funkce lm()
(linear model), o tom si ale povíme více v jiných předmětech.
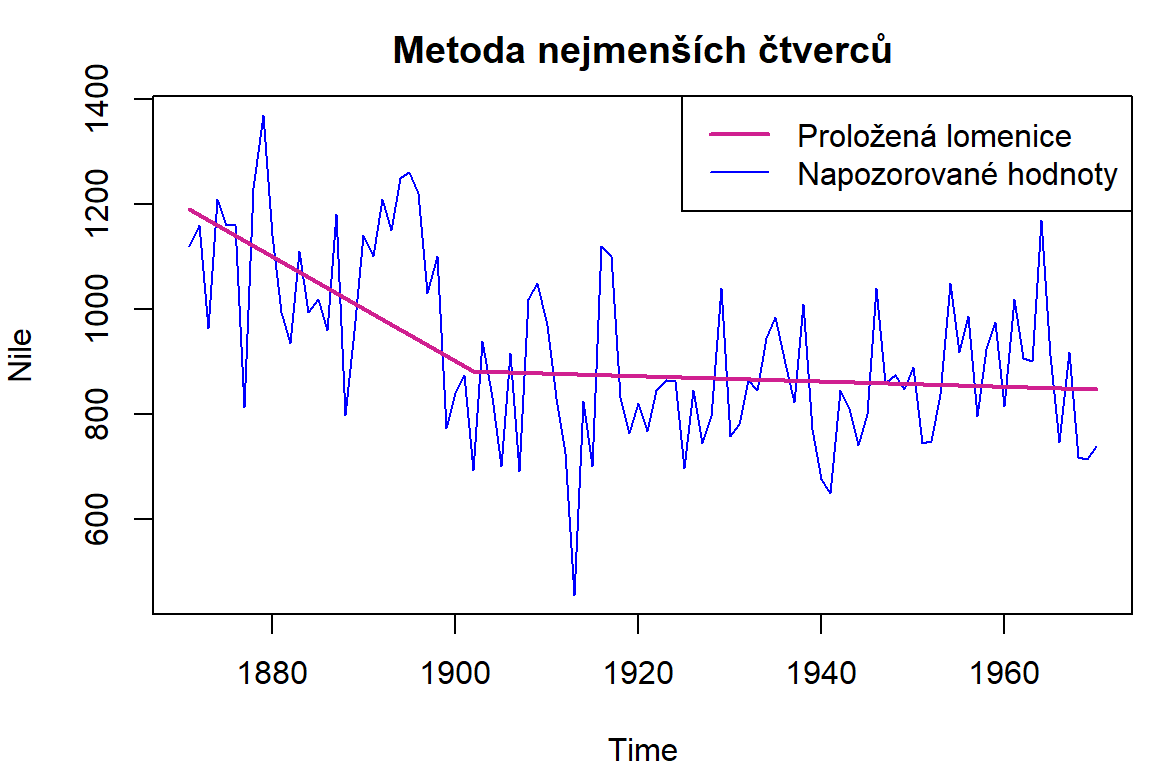
- Optim není všespásný aneb za obecnost se platí. Uvažte
časovou řadu pozorování ročního průtoku řeky Nilu v Aswanu mezi lety
1871-1970 v \(10^8~\mathrm{m}^3\) (data
Nile). Nalezněte spojitou po částech lineární funkci s jedním zlomem, která nejlépe prokládá data. Chceme tedy funkci, která splňuje
- \(f(x) = a + b x\) pro \(x \in [1871, z]\),
- \(f(x) = c + d x\) pro \(x \in [z, 1970]\),
- \(a + b z = c + d z\), kde \(z = 1902\) je rok zlomu.
Řešte opět minimalizací čtverců. Použijte spoustu jiných startovacích bodů, hrozí minutí globálního minima.
Interpretace: číselně ukažte, zda je z časové řady patrné, že výstavba přehrady v letech 1899-1902 měla nějaký vliv na roční průtok.