Cvičení 11 - Definice vlastních funkcí
Jan Vávra
Rkový skript ke stažení: R
Co si zde představíme?
- jak vytvořit vlastní funkci pomocí
function.
Základní použití function
Už jsme se s tímto příkazem setkali dříve. Například funkce typu
apply vyžadují nějakou funkci, přičemž lze použít již
nějakou v Rku dostupnou. Ale často potřebujete něco specifického, co jen
tak v Rku nenaleznete.
Narozdíl od Pythonu, v Rku chybí funkce square pro
mocnění na druhou:
square <- function(x){ # v (...) závorkách argumenty funkce, potom v {...} příkazy k provedení
x^2 # to, co bude funkcí vráceno
}
a <- 1:10
square(a) # dokud to obsah {...} bude podporovat, tak zachová vektorizaci## [1] 1 4 9 16 25 36 49 64 81 100Pozor na to, co je výstupem funkce. Neudáte-li jinak, bude to vždy ten poslední příkaz:
cube <- function(x){
- x * x * x # tento řádek "printuje" -x^3, ale není finální výstup
x^3 # za finální výstup se považuje poslední "printovaná" hodnota
}
cube(a)## [1] 1 8 27 64 125 216 343 512 729 1000Výstup funkce se jednoznačně označuje pomocí return.
Dejte ale pozor, aby takový příkaz byl až na samotném konci. Cokoliv
provedeného potom už nemá na výsledek žádný vliv.
cube <- function(x){ # přemaže předchozí znění funkce tímto novým předpisem
ret <- x * x # libovolné množství mezivýpočtů (zde neefektivní, ale aspoň pro ukázku)
ret <- ret * x # můžeme si definovat lokální proměnné (existují jen uvnitř funkce),
cat("Výpočet ukončen.") # dodatečný příkaz před return, který nebude výstupem funkce
return(ret) # příkaz, kterým jasně definuji, co je výstupem funkce
ret <- -ret # cokoliv po return je ignorováno
cat("Tohle již vidět nebude.") # cokoliv po return je ignorováno
}
a3 <- cube(a) # při zavolání také vrací text## Výpočet ukončen.Funkce ani nemusí mít žádný argument, prostě provede danou sadu příkazů:
print_cube <- function(){
for(i in 1:length(a3)){ # function může pracovat i s globálními proměnnými (tady je délka stále 10)
a3 <- c(1:5)^3 # lze lokálně měnit (délka se změní na 5)
print(a3)
}
}
print_cube()## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125
## [1] 1 8 27 64 125a3 # globálně ale zůstane proměnná nezměněná## [1] 1 8 27 64 125 216 343 512 729 1000rm(a3) # smazání proměnné (takto lze smazat třeba i funkci)
# print_cube() # nemá argument a3 a ani neexistuje globální proměnná a3 -> vrací errorFunkci můžeme předdefinovat její argument(y). Následně není třeba daný argument vyplnit a bude pracovat s danou hodnotou:
cube <- function(x = 1:4){ # defaultní hodnoty argumentu
return(x^3)
}
cube(1:10) # změna argumentu x## [1] 1 8 27 64 125 216 343 512 729 1000cube() # použití defaultní hodnoty x## [1] 1 8 27 64Funkce může mít i více argumentů:
straight_line <- function(x, a = 0, b = 1){
return(a + b*x)
}
straight_line(-3:3) # bere defaultní hodnoty pro a a b## [1] -3 -2 -1 0 1 2 3straight_line(-3:3, 2) # a se mění dle přání, b zůstává defaultní## [1] -1 0 1 2 3 4 5straight_line(-3:3, 2, -1) # změna obou argumentů v přesně daném pořadí## [1] 5 4 3 2 1 0 -1straight_line(-3:3, b = -5, a = 1) # změna obou argumentů v libovolném pořadí, je ale třeba jasně přiřadit## [1] 16 11 6 1 -4 -9 -14A <- matrix(rnorm(100), nrow = 20) # náhodná matice 20×5
apply(A, 2, straight_line) # aplikace funkce na sloupce matice A (a, b defaultní)## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.5048723 0.726710608 0.03572008 -0.3047375 1.22867182
## [2,] 0.3958758 1.067047285 -0.49796263 0.3745733 0.76804354
## [3,] 1.4155378 -1.814585236 0.27857542 -0.1811123 1.82247036
## [4,] -0.7223243 0.008796922 0.64492487 -0.4109082 -0.01583165
## [5,] -0.6183570 -0.326998699 1.44274366 -0.7798012 1.19376509
## [6,] -1.5626204 0.578129296 -0.26922856 0.6356558 1.17442143
## [7,] 0.1279588 1.219543458 -0.22781203 0.8752351 -0.93388354
## [8,] -0.1569521 -0.289854421 -0.76458865 1.9897535 0.04531086
## [9,] -1.5153363 -1.278031954 0.06429768 0.9888538 0.58651366
## [10,] 1.1616016 -0.486875912 -0.34231481 -0.4770730 -0.21269519
## [11,] -1.0616634 0.166523530 0.14537461 -0.4830316 0.63593815
## [12,] 1.0525705 -1.807374582 0.20135592 0.4783493 0.46672720
## [13,] -1.0903171 -0.959307836 1.41242471 0.8475885 -0.80534689
## [14,] -0.9504364 1.070328439 -0.77864024 0.8192277 1.12888223
## [15,] 0.1888942 0.490747416 0.77638728 -0.7575992 -0.75216731
## [16,] -1.3069128 0.183632890 -1.76681028 -0.6517043 0.40560713
## [17,] -1.0929660 -0.531039138 -0.37048304 -0.8197801 0.71840258
## [18,] 1.1674275 0.742454212 1.45310785 0.3144668 1.31154813
## [19,] 1.1981297 -2.279520776 -2.08583208 -0.6427932 -1.47244914
## [20,] -1.9625995 0.181297942 1.48620437 0.4624625 0.26347436apply(A, 1, straight_line, a = 2, b = -1) # aplikace funkce na řádky matice A s upřesněním argumentů## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 1.4951277 1.6041242 0.5844622 2.722324 2.6183570 3.5626204 1.8720412 2.15695207 3.515336 0.8383984
## [2,] 1.2732894 0.9329527 3.8145852 1.991203 2.3269987 1.4218707 0.7804565 2.28985442 3.278032 2.4868759
## [3,] 1.9642799 2.4979626 1.7214246 1.355075 0.5572563 2.2692286 2.2278120 2.76458865 1.935702 2.3423148
## [4,] 2.3047375 1.6254267 2.1811123 2.410908 2.7798012 1.3643442 1.1247649 0.01024652 1.011146 2.4770730
## [5,] 0.7713282 1.2319565 0.1775296 2.015832 0.8062349 0.8255786 2.9338835 1.95468914 1.413486 2.2126952
## [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
## [1,] 3.061663 0.9474295 3.0903171 2.9504364 1.811106 3.306913 3.092966 0.8325725 0.8018703 3.9625995
## [2,] 1.833476 3.8073746 2.9593078 0.9296716 1.509253 1.816367 2.531039 1.2575458 4.2795208 1.8187021
## [3,] 1.854625 1.7986441 0.5875753 2.7786402 1.223613 3.766810 2.370483 0.5468922 4.0858321 0.5137956
## [4,] 2.483032 1.5216507 1.1524115 1.1807723 2.757599 2.651704 2.819780 1.6855332 2.6427932 1.5375375
## [5,] 1.364062 1.5332728 2.8053469 0.8711178 2.752167 1.594393 1.281597 0.6884519 3.4724491 1.7365256apply(A, 2, straight_line, x = 9, b = -1) # místo x považuje za hlavní argument a, ten nejbližší neupřesněný## [,1] [,2] [,3] [,4] [,5]
## [1,] -8.495128 -8.273289 -8.964280 -9.304737 -7.771328
## [2,] -8.604124 -7.932953 -9.497963 -8.625427 -8.231956
## [3,] -7.584462 -10.814585 -8.721425 -9.181112 -7.177530
## [4,] -9.722324 -8.991203 -8.355075 -9.410908 -9.015832
## [5,] -9.618357 -9.326999 -7.557256 -9.779801 -7.806235
## [6,] -10.562620 -8.421871 -9.269229 -8.364344 -7.825579
## [7,] -8.872041 -7.780457 -9.227812 -8.124765 -9.933884
## [8,] -9.156952 -9.289854 -9.764589 -7.010247 -8.954689
## [9,] -10.515336 -10.278032 -8.935702 -8.011146 -8.413486
## [10,] -7.838398 -9.486876 -9.342315 -9.477073 -9.212695
## [11,] -10.061663 -8.833476 -8.854625 -9.483032 -8.364062
## [12,] -7.947429 -10.807375 -8.798644 -8.521651 -8.533273
## [13,] -10.090317 -9.959308 -7.587575 -8.152411 -9.805347
## [14,] -9.950436 -7.929672 -9.778640 -8.180772 -7.871118
## [15,] -8.811106 -8.509253 -8.223613 -9.757599 -9.752167
## [16,] -10.306913 -8.816367 -10.766810 -9.651704 -8.594393
## [17,] -10.092966 -9.531039 -9.370483 -9.819780 -8.281597
## [18,] -7.832572 -8.257546 -7.546892 -8.685533 -7.688452
## [19,] -7.801870 -11.279521 -11.085832 -9.642793 -10.472449
## [20,] -10.962600 -8.818702 -7.513796 -8.537538 -8.736526Funkce může pochopitelně vracet vícero různých hodnot v podobě listu:
popisne_charakteristiky <- function(x){
ret <- list()
ret$n <- length(x)
ret$sumNA <- sum(is.na(x))
ret[["NA%"]] <- ret$sumNA / ret$n
ret$mean <- mean(x, na.rm = TRUE)
ret$sd <- sd(x, na.rm = TRUE)
ret$quantiles <- quantile(x, probs = seq(0,1,by=0.25), na.rm = TRUE)
trim_perc <- c(0.01, 0.05)
ret$trim_mean <- sapply(trim_perc, function(p){
qs <- quantile(x, probs = c(p/2, 1-p/2))
subx <- x[(qs[1] <= x) & (x <= qs[2])]
mean(subx)
})
names(ret$trim_mean) <- paste0(100*trim_perc,"%")
return(ret)
}
popisne_charakteristiky(rgamma(1000, shape = 1.8))## $n
## [1] 1000
##
## $sumNA
## [1] 0
##
## $`NA%`
## [1] 0
##
## $mean
## [1] 1.825293
##
## $sd
## [1] 1.317367
##
## $quantiles
## 0% 25% 50% 75% 100%
## 0.03711902 0.82172608 1.58435547 2.52187434 8.84231134
##
## $trim_mean
## 1% 5%
## 1.80176 1.75393Například u funkce cor jsme viděli argument
method, který přijímá i charaktery. V
help(cor) můžeme vidět, že defaultní nastavení
method má výčet všech akceptovatelných hodnot. Přitom bez
udání method spočte funkce cor korelační
koeficient jen metodou "pearson". Toho lze docílit
následovně:
skalarni_soucin <- function(x, y, method = c("for", "sum", "prod")){
method <- match.arg(method) # vybere hodnotu argumentu v nejlepší shodě s danými možnostmi
# a bude to ta první, pokud method není udáno
cat(method, "\n") # abychom věděli jaká metoda je použita
ret <- switch(method,
"for" = {xy <- 0; for(i in 1:length(x)){xy <- xy + x[i]*y[i]}; xy},
sum = sum(as.numeric(x)*as.numeric(y)),
prod = as.numeric(t(as.numeric(x)) %*% as.numeric(y)))
# jinak pro skalární součin doporučuji používat: matrix %*% matrix,
# což zvládá více skalárních součinů najednou (každé políčko výsledné matice je vlastně skalárním součinem)
return(ret)
}
skalarni_soucin(1:2, 3:4) # použije method = "for"## for## [1] 11skalarni_soucin(1:2, 3:4, "sum") # upřesnění method na "sum"## sum## [1] 11skalarni_soucin(1:2, 3:4, "p") # ani nemusí být celé dopsané, ale pozor na podobnost (začátků stringů)## prod## [1] 11# skalarni_soucin(1:2, 3:4, "rod") # nepozná, že by měl použít methodu "prod"Někdy je třeba si defaultní hodnotu dopočítat z jiných zadaných argumentů:
moje_cut <- function(x, by = 0.25, breaks = quantile(x, probs = seq(0, 1, by = by))){
cat("Moje breaks: ", breaks, "\n")
ret <- rep(NA, length(x))
for(i in 1:(length(breaks)-1)){
inds <- (breaks[i] <= x) & (x <= breaks[i+1])
ret[inds] <- i
}
return(ret)
}
(x <- rnorm(20))## [1] -0.66277439 3.65916648 -1.36156860 1.71351057 1.84969737 2.13283299 -0.08796883 -1.47816712
## [9] 0.14633975 1.58497940 1.07495009 -0.67739626 -0.57120428 0.90645500 0.26399265 -1.37686550
## [17] -0.06039295 -0.58655328 0.58068701 -1.78119171moje_cut(x)## Moje breaks: -1.781192 -0.6664299 0.0429734 1.202457 3.659166## [1] 2 4 1 4 4 4 2 1 3 4 3 1 2 3 3 1 2 2 3 1moje_cut(x, by = 0.2)## Moje breaks: -1.781192 -0.8142307 -0.281263 0.3906704 1.610686 3.659166## [1] 2 5 1 5 5 5 3 1 3 4 4 2 2 4 3 1 3 2 4 1moje_cut(x, breaks = c(-Inf, -1, 0, 1, Inf))## Moje breaks: -Inf -1 0 1 Inf## [1] 2 4 1 4 4 4 2 1 3 4 4 2 2 3 3 1 2 2 3 1Pokud je výpočet defaultního argumentu příliš zdlouhavý na to, aby se
vešel do předpisu funkce, tak lze použít funkci missing a
dopočítat si hodnotu v těle funkce:
moje_lepsi_cut <- function(x, by = 0.25, breaks){
if(missing(breaks)){ # detekuje, zda byl argument breaks funkci předán
# provede následující příkaz jedině, když breaks nebylo funkci předáno
breaks <- quantile(abs(x), probs = seq(0, 1, by = by))
breaks <- c(-rev(breaks[-1]), 0, breaks[-1]) # symetrické hranice
breaks[1] <- -Inf
breaks[length(breaks)] <- Inf
}
cat("Moje breaks: ", breaks, "\n")
ret <- rep(NA, length(x))
for(i in 1:(length(breaks)-1)){
inds <- (breaks[i] <= x) & (x <= breaks[i+1])
ret[inds] <- i
}
return(ret)
}
x <- rnorm(1000)
table(moje_lepsi_cut(x))## Moje breaks: -Inf -1.181165 -0.6989483 -0.3462284 0 0.3462284 0.6989483 1.181165 Inf##
## 1 2 3 4 5 6 7 8
## 113 113 137 122 128 113 137 137table(moje_lepsi_cut(x, by = 0.2))## Moje breaks: -Inf -1.325732 -0.8449056 -0.5347353 -0.2744475 0 0.2744475 0.5347353 0.8449056 1.325732 Inf##
## 1 2 3 4 5 6 7 8 9 10
## 93 92 91 109 100 100 91 109 108 107table(moje_lepsi_cut(x, breaks = c(-Inf, -1, 0, 1, Inf)))## Moje breaks: -Inf -1 0 1 Inf##
## 1 2 3 4
## 150 335 340 175Někdy chceme využít argumenty jiných funkcí, jen se nám je nechce
všechny vypisovat do definice funkce. Můžeme si udělat zkratku pomocí
...:
mrizky_plot <- function(x, y, col.mriz = "grey", lty.mriz = 3, ...){
# Cílem této funkce je vykreslení mřížek do grafu.
# To ale musí být provedeno před nanesením bodů, protože jinak jsou čáry před body.
op <- par() # původní nastavení grafických parametrů
par(mar = c(4,4,2.5,0.5))
# vykreslení úplně prázdného plotu - ale už bude existovat
plot(x, y, type = "n", bty = "n", xaxt = "n", yaxt = "n", xlab = "", ylab = "",
xlim = range(x), ylim = range(y))
# přidání mřížek
abline(h = pretty(range(y)), col = col.mriz, lty = lty.mriz)
abline(v = pretty(range(x)), col = col.mriz, lty = lty.mriz)
par(new = TRUE) # úprava grafických parametrů pro tuto funkci
# zajistí, že se funkcí plot bude kreslit do stejného obrázku
plot(x, y, ...) # podstatná část - použij znovu plot
par(op) # přenastavení grafických parametrů na původní hodnoty
}
x <- rnorm(30)
y <- rnorm(30)
par(mfrow = c(1,2))
plot(x, y)
mrizky_plot(x, y)
mrizky_plot(x, y, col.mriz = "darkslategrey", lty.mriz = 2)
mrizky_plot(x, y, col.mriz = "darkslategrey", lty.mriz = 2,
pch = 16, cex = 1.5, col = "goldenrod") # lze posílat i jiné argumenty
# jen je problém při změně xlim a ylim
# protože mřížky tam jsou již předkreslené (teď v nezaokrouhlených hodnotách)
mrizky_plot(x, y, col.mriz = "darkslategrey", lty.mriz = 2,
xlim = c(0,3), ylim = c(-1,3), pch = 16, cex = 1.5, col = "goldenrod")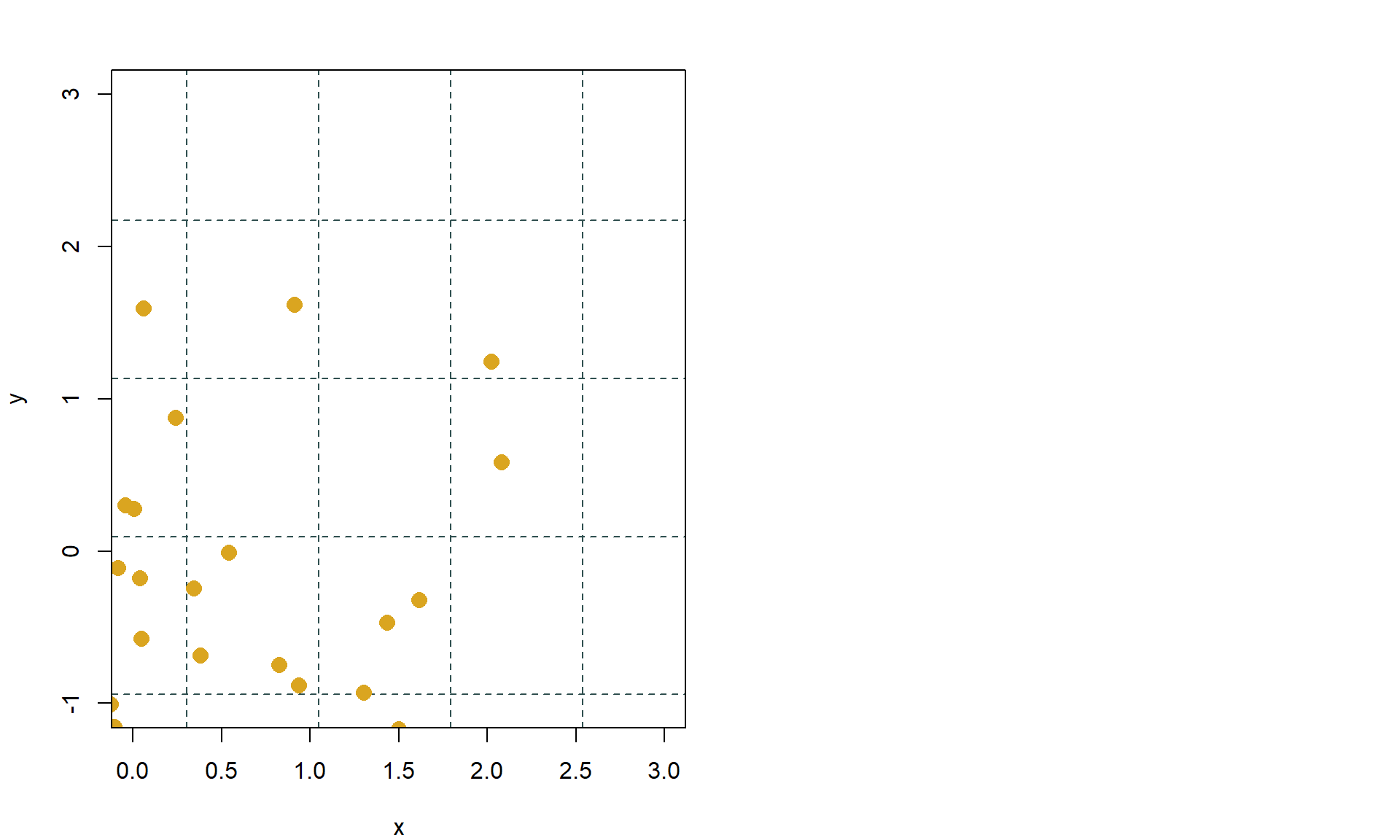
Už jsme měli tu možnost narazit na funkce, které odmítnou pracovat či
vrátí warning. Pokud chcete své budoucí já varovat, že provádíte něco
napatřičného, je dobré tuto “blbuvzdornost” naimplementovat do svých
funkcí. Nejprve si ukážeme jak detekovat, zda dojde k error
či warning:
# Pomocí funkce try lze detekovat pouze `error`
(x <- try(log(10))) # pokud bez problému, tak vrátí přímo tu hodnotu## [1] 2.302585class(x)## [1] "numeric"is(x, "try-error")## [1] FALSE(y <- try(log(0, base = 0))) # projde s warning, ale vrátí NaN## Warning in doTryCatch(return(expr), name, parentenv, handler): NaNs produced## [1] NaNclass(y)## [1] "numeric"is(y, "try-error")## [1] FALSE(a <- try(log("a"))) # vrátí errorovou hlášku pod jinou třídou## Error in log("a") : non-numeric argument to mathematical function## [1] "Error in log(\"a\") : non-numeric argument to mathematical function\n"
## attr(,"class")
## [1] "try-error"
## attr(,"condition")
## <simpleError in log("a"): non-numeric argument to mathematical function>class(a)## [1] "try-error"is(a, "try-error")## [1] TRUE# Obecnější funkcí je tryCatch, ale vyžaduje podání funkcí pro error a warning
my_error_function <- function(e){message("Error found: ", conditionMessage(e))}
my_warning_function <- function(w){message("Warning triggered: ", conditionMessage(w))}
(x <- tryCatch(log(10), error = my_error_function, warning = my_warning_function))## [1] 2.302585class(x)## [1] "numeric"is(x, "warning") || is(x, "error")## [1] FALSE(y <- tryCatch(log(0, base = 0), error = my_error_function, warning = my_warning_function))## Warning triggered: NaNs produced## NULLclass(y)## [1] "NULL"is(y, "warning") || is(y, "error")## [1] FALSE(a <- tryCatch(log("a"), error = my_error_function, warning = my_warning_function))## Error found: non-numeric argument to mathematical function## NULLclass(a)## [1] "NULL"is(a, "warning") || is(a, "error")## [1] FALSEJak napsat funkci tak, aby vrátila error či warning?
sqrt_abs <- function(x){
# Funkce spočítá odmocninu z x
# Pokud záporné x, tak vrátí warning, ale aspoň spočte sqrt(-x)
if(!is.numeric(x)){
stop("Input must be a numeric value.") # zastaví výpočet a vytiskne errorovou hlášku
}
if(x < 0){
x <- abs(x) # provedení absolutní hodnoty
warning("The negative input value has been transformed to positive.\n") # výpočet pokračuje dál
}
result <- sqrt(x)
message("Calculation complete.")
return(result)
}
sqrt_abs(16); sqrt(abs(16)) # naše verze informuje o ukončení výpočtu## Calculation complete.## [1] 4## [1] 4sqrt_abs(-9); sqrt(abs(-9)) # naše verze vrací warning ## Warning in sqrt_abs(-9): The negative input value has been transformed to positive.## Calculation complete.## [1] 3## [1] 3# sqrt_abs("hello"); sqrt(abs("hello")) # obojí vrací errorVýpočty někdy mohou trvat drahnou chvíli. Pokud je součástí nějaký iterační proces, je možné nastavit informační hlášku o tom, kolik procent již bylo spočteno. Ale používejte jen, když to je opravdu užitečné a zbytečně to nezpomaluje proces, jako zde:
x <- rnorm(1e6)
calculate <- function(x){
n <- length(x)
pb <- txtProgressBar(min = 0, max = n, style = 3) # započetí progresu výpočtu
y <- numeric(n)
for(i in 1:n){
y[i] <- log(abs(sin(cos(x[i])))) # špatný nápad počítat to takto for cyklem, raději vektorově po složkách
setTxtProgressBar(pb, i) # upravení progresu výpočtu (zde neustálé opakování zdržuje funkci)
}
return(y)
close(pb) # ukončení progresu výpočtu
message("Done!")
}
y <- calculate(x)## | | | 0% | |= | 1% | |== | 2% | |=== | 3% | |==== | 4% | |===== | 5% | |====== | 6% | |======= | 7% | |======== | 8% | |========= | 9% | |========== | 10% | |=========== | 11% | |============ | 12% | |============= | 13% | |============== | 14% | |=============== | 15% | |================ | 16% | |================= | 17% | |================== | 18% | |=================== | 19% | |==================== | 20% | |===================== | 21% | |====================== | 22% | |======================= | 23% | |======================== | 24% | |========================= | 25% | |========================== | 26% | |=========================== | 27% | |============================ | 28% | |============================= | 29% | |============================== | 30% | |=============================== | 31% | |================================ | 32% | |================================= | 33% | |================================== | 34% | |=================================== | 35% | |==================================== | 36% | |===================================== | 37% | |====================================== | 38% | |======================================= | 39% | |======================================== | 40% | |========================================= | 41% | |========================================== | 42% | |=========================================== | 43% | |============================================ | 44% | |============================================= | 45% | |============================================== | 46% | |=============================================== | 47% | |================================================ | 48% | |================================================= | 49% | |================================================== | 50% | |=================================================== | 51% | |==================================================== | 52% | |===================================================== | 53% | |====================================================== | 54% | |======================================================= | 55% | |======================================================== | 56% | |========================================================= | 57% | |========================================================== | 58% | |=========================================================== | 59% | |============================================================ | 60% | |============================================================= | 61% | |============================================================== | 62% | |=============================================================== | 63% | |================================================================ | 64% | |================================================================= | 65% | |================================================================== | 66% | |=================================================================== | 67% | |==================================================================== | 68% | |===================================================================== | 69% | |====================================================================== | 70% | |======================================================================= | 71% | |======================================================================== | 72% | |========================================================================= | 73% | |========================================================================== | 74% | |=========================================================================== | 75% | |============================================================================ | 76% | |============================================================================= | 77% | |============================================================================== | 78% | |=============================================================================== | 79% | |================================================================================ | 80% | |================================================================================= | 81% | |================================================================================== | 82% | |=================================================================================== | 83% | |==================================================================================== | 84% | |===================================================================================== | 85% | |====================================================================================== | 86% | |======================================================================================= | 87% | |======================================================================================== | 88% | |========================================================================================= | 89% | |========================================================================================== | 90% | |=========================================================================================== | 91% | |============================================================================================ | 92% | |============================================================================================= | 93% | |============================================================================================== | 94% | |=============================================================================================== | 95% | |================================================================================================ | 96% | |================================================================================================= | 97% | |================================================================================================== | 98% | |=================================================================================================== | 99% | |====================================================================================================| 100%Závěrem bych chtěl upozornit na následující konvenci. Každou funkci,
která za to stojí, si uložte do separátního souboru pojmenovaného
jmeno_funkce.R. Příslušný skript bude obsahovat jen tělo
funkce. Nezapomeňte si okomentovat veškeré vstupní argumenty (co
představují, jaké hodnoty se očekávají), ale také co je účelem a
výstupem funkce. Vlastní funkce si schraňujte ve speciálním adresáři s
implementovanými funkcemi. Funkci si nahrajete do vašeho prostředí
pomocí source():
# Nejprve si nastavíme adresář.
WD <- getwd()
dir_fun <- file.path(dirname(WD), "fun")
dir.create(dir_fun) # pokud ještě neexistuje
# Takto se funkce ukládá do souboru.
dump("mrizky_plot", file = file.path(dir_fun, "mrizky_plot.R"))
# a tímto příkazem si ji smažeme z našeho prostředí (abychom pak ukázali, že source ji nahraje)
rm("mrizky_plot")
is.element("mrizky_plot", ls())## [1] FALSE# Takto se funkce načítá ze souboru.
source(file.path(dir_fun, "mrizky_plot.R"))
is.element("mrizky_plot", ls())## [1] TRUEÚložky na procvičení
Vyřešte si to sami, aniž byste se dívali do řešení (úplně dole vespod skriptu).
- Vytvořte si vlastní funkci, která vrací paletu
nbarev. Předpokládejte, že si zvolíte 2 hraniční barvy, ostatní barvy ekvidistantně rozdělte podle hodnot RGB. Barva se dá převést do RGB pomocí funkcecol2rgb(). Ze tří čísel se dá vyrobit barva pomocí funkcergb():
barvy_jako_cisla <- col2rgb(c("olivedrab1", "tomato"))
nova_barva_ve_stredu <- rgb(red = mean(barvy_jako_cisla["red",]),
green = mean(barvy_jako_cisla["green",]),
blue = mean(barvy_jako_cisla["blue",]),
maxColorValue = 255)
par(mar = c(0,0,0,0), mfrow = c(1,1))
plot(0,0)
rect(-1, -1, 1, 1, col = nova_barva_ve_stredu) Funkci pak zobecněte pro libovolný počet zadaných barev.
Funkci pak zobecněte pro libovolný počet zadaných barev.
- Ve cvičení 5
jsme si konstruovali tabulku pro data. Přetvořte to jako funkci
vytvor_tabulkus následujícími argumenty:
- různé hodnoty (a jejich počet) \(K\), scénářů a \(n\),
- seznamy matic \(X\) a \(Y\),
- cesta k výslednému souboru,
- počet platných číslic (zvlášť pro průměr a směrodatnou odchylku),
- zda se má směrodatná odchylka zapsat menším fontem
- a případné další modifikace.
Ve cvičení 10 jsme si zavedli nový typ grafu “počítadlo”. Napište novou funkci
plot.pocitadlo, která vyrobí obrázek pro zadaná data. Přidejte několik kosmetických argumentů pro tuto funkci, např. počet kuliček (s vhodnou defaultní hodnotou) a varujte uživatele, který zadá nízký počet kuliček.Napište si funkci
hraj_game, která simuluje jeden game v tenisu, kde podávající hráč má danou pravděpodobnost výhry jednoho fifteenu. Vracet by mohla nejen informaci o vítězi gamu, ale také skóre, počet game ballů, shod, zda to byl kanár, atd. Posléze ji rozšiřte o další parametry:
- pravděpodobnosti výhry fifteenu pro hráče 1, jestliže podává on a jestliže soupeř,
- informaci o tom, kdo je podávající,
- a informaci o tom, zda se jedná o tiebreak.
Pokračujte dál a napište si funkce hraj_set a
hraj_zapas, kde vždy využijete předchozích funkcí. Funkce
hraj_zapas by pak měla vrátit užitečné statistické údaje za
celý zápas.
Koho to opravdu zaujalo, tak může napsat ještě jednu funkci
simuluj_zapasy, která provede simulační studii opakováním
her zápasů se zadanými pravděpodobnostmi. Vracet by měla
data.frame obsahující statistiky z jedno zápasu na jednom
řádku. Pomocí empirických odhadů pravděpodobností odpovězte na
následující otázky:
- Jaká je pravděpodobnost, že zápas vyhraje někdo, kdo celkově vyhrál méně fifteenů?
- Průměrně se očekává 45 sekund na jeden fifteen. S jakou pravděpodobností bude zápas trvat přes 3 hodiny?
- Jaké je rozdělení počtu shod či kanárů za jeden zápas?
- Jak se liší výsledky pro absolutně vyrovnané hráče, pro hráče se stejnou výhodou na podání a pro případ, když jeden hráče j pravděpodobnostně lepší než druhý?