Zpět na přehled cvičení

Rkový skript ke stažení: R

Co si zde představíme?

Pravděpodobnostní rozdělení - základní přehled

Nepřesně řečeno, pravděpodobnostní rozdělení \(\mathsf{P}_X\) udává jaké hodnoty může náhodná veličina \(X\) nabývat s jakou pravděpodobností. Lze jej určit hned několika způsoby:

Rodiny diskrétních rozdělení dostupných v Rku:

Zde je vykreslení základních funkcí pro binomické rozdělení \(\mathsf{Bi}(20, 0.34)\):

par(mfrow = c(1,3), mar = c(4,4,2.5,0.5))  # 3 obrázky vedle sebe s malými okraji

# Distribuční funkce - pro diskrétní rozdělení skokovitá
x <- 0:20                                 # možné hodnoty náhodné veličiny
Fx <- pbinom(x, size = 20, prob = 0.34)   # distr. fce skáče jen v hodnotách x (stačí znát jen ty)
plot(x, Fx, type = "s", main = "Distribuční funkce Bi(20, 0.34)")
abline(h = c(0,1), col = "grey", lty = 2) # sevřená zdola 0 a shora 1
abline(v = 20 * 0.34, col = "red")        # střední hodnota

# Hustota - pro diskrétní rozdělení jen pravděpodobnosti nabytí hodnoty
fx <- dbinom(x, size = 20, prob = 0.34) 
plot(x, fx, type = "h", main = "Hustota Bi(20, 0.34)")
abline(v = 20 * 0.34, col = "red")        # střední hodnota

# Kvantilová funkce - skokovitá stejně jako distribuční funkce
q <- qbinom(Fx, size = 20, prob = 0.34)
# all.equal(q, x) # stejné jako x
plot(Fx, q, type = "s", main = "Kvantilová funkce Bi(20, 0.34)")
abline(h = 20 * 0.34, col = "red")        # střední hodnota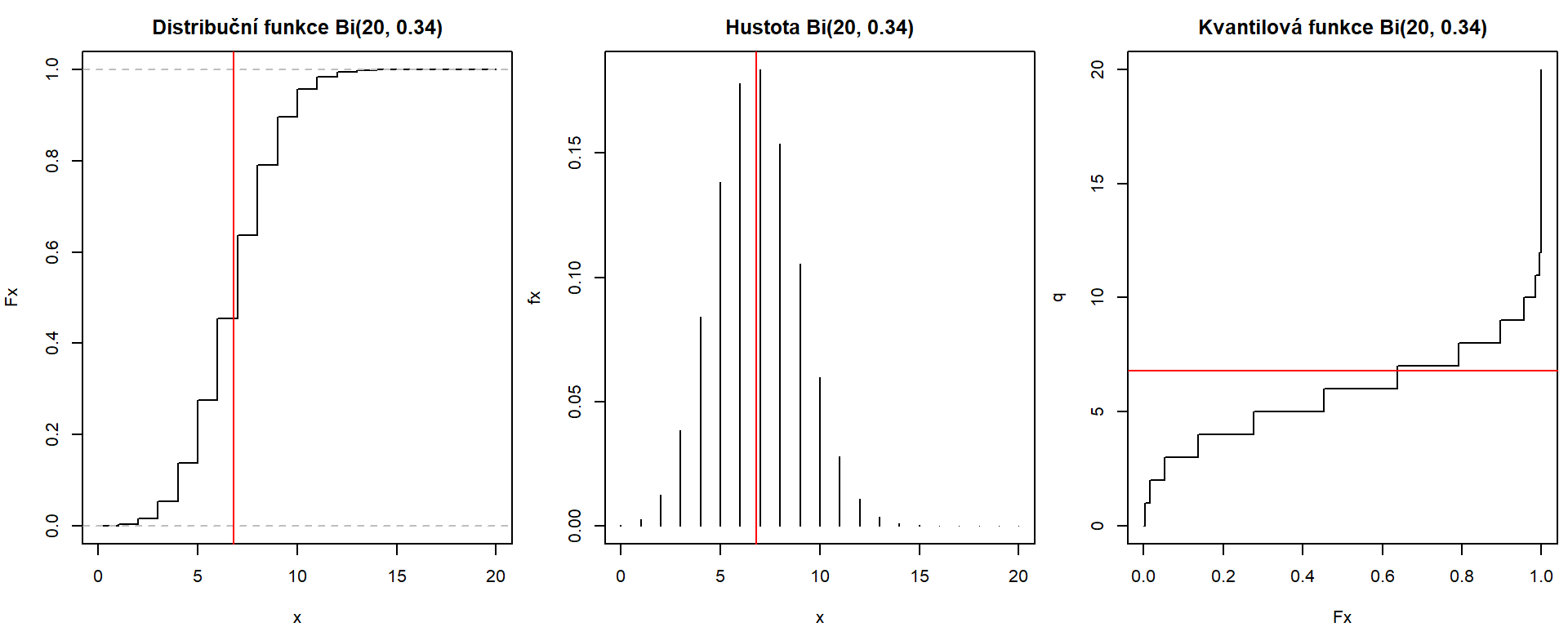

Rodiny spojitých rozdělení dostupných v Rku:

Zde je vykreslení základních funkcí pro normální rozdělení \(\mathsf{N}(5, 2^2)\):

par(mfrow = c(1,3), mar = c(4,4,2.5,0.5))  # 3 obrázky vedle sebe s malými okraji

# Distribuční funkce - ryze rostoucí funkce na celém R
x <- seq(-1, 11, length.out = 1001)           # rozumná volba hodnot
Fx <- pnorm(x, mean = 5, sd = 2)              # distr. fce ve zvolených hodnotách
plot(x, Fx, type = "l",                       # propojí body mezi sebou úsečkou
     main = "Distribuční funkce N(5, 2^2)")
abline(h = c(0,1), col = "grey", lty = 2)     # sevřená zdola 0 a shora 1
abline(v = 5, col = "red")                    # střední hodnota

# Hustota - pro diskrétní rozdělení jen pravděpodobnosti nabytí hodnoty
fx <- dnorm(x, mean = 5, sd = 2) 
plot(x, fx, type = "l", main = "Hustota N(5, 2^2)")
abline(v = 5, col = "red")                    # střední hodnota

# Kvantilová funkce - skokovitá stejně jako distribuční funkce
probs <- seq(0.001, 0.999, by = 0.001)
q <- qnorm(probs, mean = 5, sd = 2)
plot(probs, q, type = "l", main = "Kvantilová funkce N(5, 2^2)")
abline(v = c(0,1), col = "grey", lty = 2)     # definiční obor na (0, 1)
abline(h = 5, col = "red")                    # střední hodnota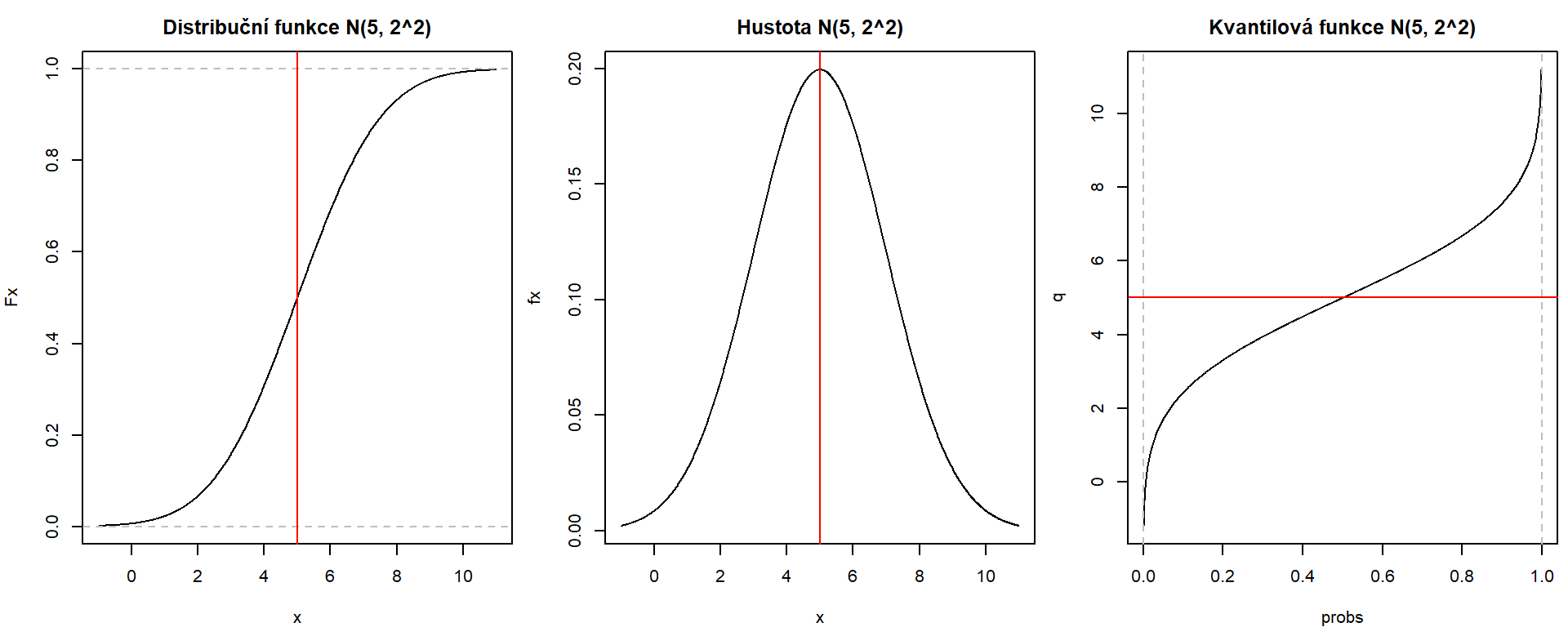

Nyní pár technických poznámek k představeným funkcím.

Prvním argumentem je hlavní proměnná zadané funkce. Pak následují argumenty upřesňující konkrétního člena pravděpodobnostní rodiny, vizte přehled výše. Pro distribuční a kvantilovou funkci máme jako další parametr logickou hodnotu lower.tail udávájící, zda se za distribuční funkci považuje dolní chvost (tedy \(\mathsf{P}(X \leq x)\)) či horní chvost \(\mathsf{P}(X > x)\) (někdy definováno takto). Dále logický argument log či log.p udává, zda vracet výsledek na logaritmické škále, která se dá často vyjádřit jednodušeji. To lze využít například pro odhady parametrů metodou maximální věrohodnosti.

Ukažme si to na příkladu exponenciálního rozdělení s parametrem 2:

x <- c(0.5, 1, 2)                      # funkce fungují i vektorově po složkách
pexp(x, rate = 2)                      # P(Exp(2) <= x)
## [1] 0.6321206 0.8646647 0.9816844
1 - exp(-x * 2)                        # ručně spočteno
## [1] 0.6321206 0.8646647 0.9816844
pexp(x, rate = 2, lower.tail = FALSE)  # P(Exp(2) > x)  - sečte se s tím předchozím na 1
## [1] 0.36787944 0.13533528 0.01831564
exp(-x * 2)                            # ručně spočteno
## [1] 0.36787944 0.13533528 0.01831564
dexp(x, rate = 2)                      # hustota Exp(2) v hodnotách x
## [1] 0.73575888 0.27067057 0.03663128
2 * exp(-x * 2)                        # ručně spočteno  
## [1] 0.73575888 0.27067057 0.03663128
dexp(x, rate = 2, log = TRUE)          # log-hustota Exp(2) v hodnotách x
## [1] -0.3068528 -1.3068528 -3.3068528
log(2) - 2*x                           # ručně spočteno
## [1] -0.3068528 -1.3068528 -3.3068528
p <- c(0.3, 0.6, 0.8)                  # pravděpodobnosti v intervalu (0, 1)
qexp(p, rate = 2)                      # kvantily zadaných pravděpodobností pro Exp(2)
## [1] 0.1783375 0.4581454 0.8047190
-log(1-p)/2                            # ručně spočteno
## [1] 0.1783375 0.4581454 0.8047190
qexp(p, rate = 2, lower.tail = FALSE)  # kvantily doplňkových pravděpodobností pro Exp(2)
## [1] 0.6019864 0.2554128 0.1115718
-log(p)/2                              # ručně spočteno
## [1] 0.6019864 0.2554128 0.1115718

Generování (pseudo) náhodných čísel

První věcí, kterou je třeba si uvědomit, že software sice umí generovat zdánlivě náhodná čísla, ale nakonec se jedná o deterministický algoritmus. Ten je kompletně přeurčen jedním jediným číslem, které se dá nastavit pomocí příkazu set.seed(). Jakmile je číslo nastaveno, všechno náhodné generování od té doby proběhne stejně. Přesvědčte se na následující sekvenci příkazů:

sample(1:6, 3, replace = TRUE)             # 3 hody kostkou
## [1] 3 3 2
set.seed(123456789)        # nastavení náhodného generátoru
sample(1:6, 3, replace = TRUE)
## [1] 4 2 3
sample(1:6, 3, replace = TRUE)
## [1] 4 5 6
set.seed(314159)           # přenastavení náhodného generátoru
sample(1:6, 3, replace = TRUE)
## [1] 2 2 4
set.seed(123456789)        # znovunastavení náhodného generátoru
sample(1:6, 3, replace = TRUE)
## [1] 4 2 3
set.seed(314159)           # znovunastavení náhodného generátoru
sample(1:6, 3, replace = TRUE)
## [1] 2 2 4

Toto je užitečné při provádění simulačních studií, neboť to zaručuje replikovatelnost výsledků. Doporučuje se nastavit set.seed() vždy jen jednou na začátku skriptu. Nikdy nenastavujte v cyklu!

for(i in 1:5){
  set.seed(123456)            # nastaví se pokaždé znovu na stejné číslo
  print(sample(1:6, 3, replace = TRUE))
}
## [1] 4 2 2
## [1] 4 2 2
## [1] 4 2 2
## [1] 4 2 2
## [1] 4 2 2

Nyní se zaměřme na to, jak generovat náhodná čísla. Začněme s funkcí sample(), která se zde již několikrát objevila.

Ukažme si to na příkladech:

table(sample(0:1, 2000, replace = TRUE))      # 2000 hodů spravedlivou mincí
## 
##    0    1 
## 1017  983
table(sample(1:6, 6000, replace = TRUE))      # 6000 hodů spravedlivou kostkou 
## 
##    1    2    3    4    5    6 
## 1029  956 1031 1050  987  947
# existuje verze sample.int, které stačí dát pouze horní hranici n a generuje z hodnot 1:n
table(sample.int(12, 12000, replace = TRUE))  # 12000 hodů spravedlivou 12-stěnnou kostkou
## 
##    1    2    3    4    5    6    7    8    9   10   11   12 
## 1023  983 1013  985  937  957 1002  961 1076 1009 1020 1034
table(sample(letters, 30, replace = TRUE))    # funguje i na vektor stringů
## 
## a b c e f g h i k l m n o p q r s t w x y 
## 1 1 1 1 2 1 1 3 2 1 1 1 3 1 3 2 1 1 1 1 1
table(sample(letters, 10))                    # bez opakování
## 
## c e f i j k o p r x 
## 1 1 1 1 1 1 1 1 1 1
sample.int(10)                                # náhodná permutace (náhodně 10 prvků z 10 bez opakování)
##  [1]  5 10  8  6  2  1  4  3  9  7
table(sample(0:1, 2000, replace = TRUE, prob = c(0.1, 0.9))) # 2000 hodů nespravedlivou mincí
## 
##    0    1 
##  195 1805
table(sample(1:6, 2100, replace = TRUE, prob = 1:6))         # prob se nemusí vysčítat na 1 (přeškáluje samo)
## 
##   1   2   3   4   5   6 
## 110 212 280 404 489 605
# A co se stane, pakliže se nějaké prvky v x opakují?
x <- c(letters[1:6], letters[1:4], letters[1:2])
(TAB <- table(x))
## x
## a b c d e f 
## 3 3 2 2 1 1
table(sample(x, 12000, replace = TRUE))       # je to úměrné frekvenci prvků v x
## 
##    a    b    c    d    e    f 
## 3088 2936 1976 2034  972  994
table(sample(x, 12000, replace = TRUE,        # i tu lze přenastavit pomocí prob (udáním pro každé x)
             prob = 1/TAB[x]))                # zde zpět na rovnoměrné rozdělení
## 
##    a    b    c    d    e    f 
## 2018 1959 1999 2017 1997 2010

Pro generování z jiných pravděpodobnostních rozdělení máme funkce typu r***(), kde místo hvězdiček patří příslušné jméno rodiny rozdělení, vizte výše. První argument n udává počet hodnot k vygenerování a pak následují parametry rozdělení.

runif(20, -1, 0.2)            # 20 hodnot z rovnoměrného rozdělení na intervalu (-1, 0.2)
##  [1] -0.59946858 -0.49119437 -0.65051261 -0.06916564  0.18204813 -0.24709467 -0.04792623 -0.31415680
##  [9]  0.15528202 -0.68390676 -0.90820460  0.09561238 -0.60924333 -0.66423881  0.11405955 -0.42175977
## [17] -0.10455720 -0.54558447 -0.16287947  0.10149235
rnorm(10)                     # 10 hodnot ze standardního normálního rozdělení N(0,1)
##  [1] -1.50266891 -0.03224889 -1.04729408  1.00720004 -0.94126067 -0.18967091 -1.64470736 -1.46120034
##  [9]  1.04602474 -0.40744467
rnorm(10, 5, 3)               # 10 hodnot z normálního rozdělení se střední hodnotou 5 
##  [1] 4.1564730 2.9857222 7.2251809 1.1379074 6.4433736 4.5246597 1.7407738 0.5588706 3.0529798 3.1317504
                              #             a směrodatnou odchylkou 3, tedy N(5, 3^2)
5+3*rnorm(10)                 # 10 hodnot z toho samého rozdělení jako výše (jen jiná čísla) 
##  [1]  4.3887341  1.1339145 11.5157636  5.2295457  6.9618875  2.1845687  4.8507566  7.4558148  6.7214698
## [10] -0.4190689
x <- rgamma(1000, shape = 1.9, scale = 0.7)   # 1000 hodnot z gamma rozdělení
# histogram se skutečnou křivkou hustoty
hist(x, freq = FALSE)
curve(dgamma(x, shape = 1.9, scale = 0.7), from = 0.01, to = 5, add = TRUE, col = "red")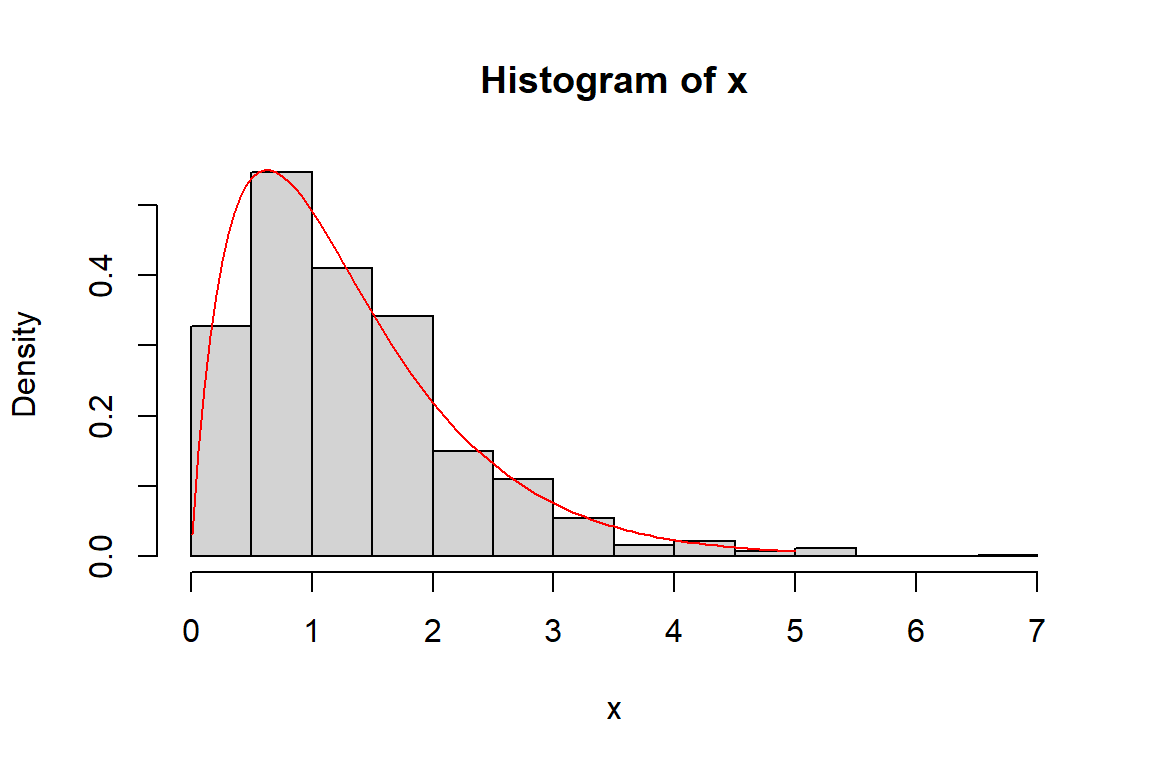

Další užitečnou funkcí pro simulační studie je funkce replicate, která umožňuje obejít for cyklus pro opakování té samé simulace:

# první argument n = počet opakovaní, dále následuje příkaz, který se má n× zopakovat
replicate(5, sample(0:1, 3, replace = TRUE))     # 5× 3 hody spravedlivou mincí  --> matice 3×5
##      [,1] [,2] [,3] [,4] [,5]
## [1,]    0    0    0    0    1
## [2,]    1    0    0    1    0
## [3,]    0    1    0    1    1
replicate(10, runif(7, -1, 1))                   # 10× 7 náhodných čísel z intervalu (-1,1) --> matice 7×10 
##            [,1]       [,2]       [,3]        [,4]       [,5]        [,6]       [,7]       [,8]        [,9]
## [1,]  0.8499585  0.3921398 -0.5530216 -0.06553976  0.4693556 -0.53392334 -0.5931093  0.7551099 -0.22828537
## [2,] -0.9515856  0.3811736  0.1651176  0.44502558 -0.3893412 -0.98870767 -0.4191338 -0.4023398 -0.62702490
## [3,]  0.8805835  0.2861470 -0.4775134  0.11329954  0.7214914 -0.77263308  0.9954939 -0.1045144 -0.52361256
## [4,] -0.9991905  0.6360379  0.1283757 -0.40851107  0.4246768  0.80412501 -0.9169828 -0.3009377  0.85674781
## [5,]  0.4326817  0.6446204  0.3200652 -0.91386633 -0.9384742  0.26652590 -0.8653268  0.7225262  0.09386081
## [6,] -0.2133063 -0.1789736  0.8682507 -0.45313164 -0.4419792 -0.09666601  0.3695359  0.4005044 -0.56979046
## [7,] -0.5068252  0.3562534  0.8475274  0.22113649  0.9479068  0.81090442  0.2724352 -0.1224595  0.01026602
##            [,10]
## [1,]  0.73819333
## [2,]  0.61323739
## [3,]  0.38882370
## [4,] -0.76802710
## [5,]  0.86902657
## [6,]  0.07811142
## [7,]  0.27858543

Základní statistické funkce

Funkce výše byly navržené pro práci s teoretickými pravděpodobnostními rozděleními. V praxi ale míváme daná data a jen ze statistických vlastností usuzujeme o jejich skutečném rozdělení. K tomu jsou užitečné následující výběrové statistiky:

x <- rnorm(200, 5, 3)          # náhodný výběr z N(5, 3^2)
mean(x)                        # aritmetický průměr
## [1] 4.913426
mean(x, trim = 0.1)            # useknutý aritmetický průměr
## [1] 4.857468
var(x)                         # výběrový rozptyl 1/(n-1) sum (X_i - mean(X))^2
## [1] 9.845333
1/(length(x) - 1) * sum((x - mean(x))^2)
## [1] 9.845333
sd(x)                          # výběrová směrodatná odchylka (odmocnina z výběrového rozptylu)
## [1] 3.137727
median(x)                      # výběrový medián
## [1] 4.732081
quantile(x, probs = c(0.05, 0.25, 0.75, 0.95)) # výběrové kvantily zadaných pravděpodobností
##         5%        25%        75%        95% 
##  0.3463886  2.8586169  7.1402073 10.2915717
min(x)                         # výběrové minimum
## [1] -2.793003
max(x)                         # výběrové maximum
## [1] 12.93891
range(x)                       # rozpětí (min a max)
## [1] -2.793003 12.938914
IQR(x)                         # interkvantilové rozpětí - vzálenost mezi 3. a 1. kvartilem (Q3 - Q1)
## [1] 4.28159
summary(x)                     # soubor několika výběrových statistik (základní popisné statistiky)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  -2.793   2.859   4.732   4.913   7.140  12.939
plot(ecdf(x))                  # empirická distribuční funkce (obrázek)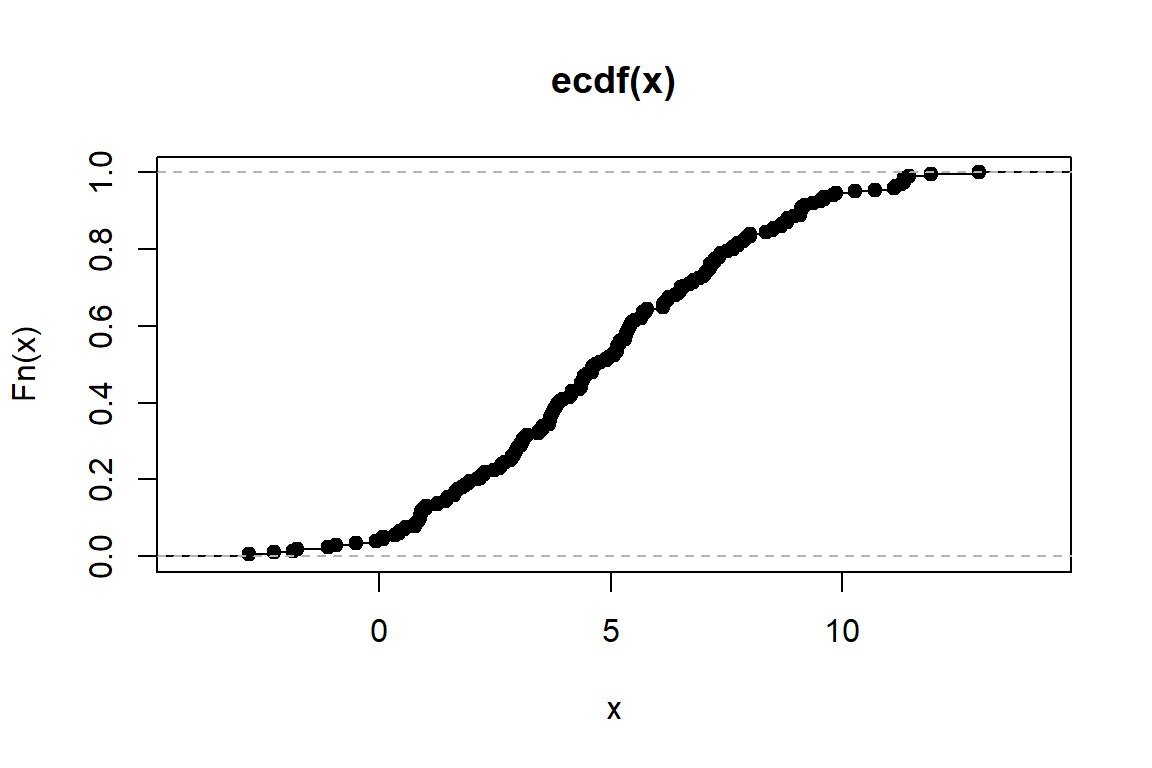

plot(acf(x))                   # autokorelační funkce (obrázek)

y <- rnorm(200, 5, 3)          # další náhodný výběr z N(5, 3^2)
cov(x, y)                      # výběrová kovariance X a Y
## [1] 0.06039245
cor(x, y)                      # výběrový Pearsonův korelační koeficient
## [1] 0.007280715
cov(cbind(x, y))               # výběrová kovarianční matice
##            x          y
## x 9.84533314 0.06039245
## y 0.06039245 6.98854718
cor(cbind(x, y))               # výběrová korelační matice
##             x           y
## x 1.000000000 0.007280715
## y 0.007280715 1.000000000

Pro práci s kategoriálními daty je vhodná funkce table, která vytváří (kontingenční) tabulku četností. Funguje nehledě na faktorovost proměnné:

z <- sample(1:6, 200, replace = TRUE)          # opakované hody kostkou
table(z)                                       # tabulka četností
## z
##  1  2  3  4  5  6 
## 36 30 39 32 33 30
proportions(table(z))                          # tabulka relativních četností
## z
##     1     2     3     4     5     6 
## 0.180 0.150 0.195 0.160 0.165 0.150
prop.table(table(z))                           # tabulka relativních četností
## z
##     1     2     3     4     5     6 
## 0.180 0.150 0.195 0.160 0.165 0.150
w <- sample(0:1, 200, replace = TRUE)          # nezávislé hody mincí
table(z, w)                                    # dvourozměrná tabulka pro každou kombinaci znaků
##    w
## z    0  1
##   1 16 20
##   2 11 19
##   3 19 20
##   4 16 16
##   5 14 19
##   6 16 14
prop.table(table(z, w))                        # tabulka relativních četností pro každou kombinaci znaků
##    w
## z       0     1
##   1 0.080 0.100
##   2 0.055 0.095
##   3 0.095 0.100
##   4 0.080 0.080
##   5 0.070 0.095
##   6 0.080 0.070
chisq.test(table(z, w))                        # Chí-kvadrát test nezávislosti
## 
##  Pearson's Chi-squared test
## 
## data:  table(z, w)
## X-squared = 2.2286, df = 5, p-value = 0.8167

V závislosti na tom, zda se jedná o numeric či factor hodnotu se chová funkce summary odlišně:

table(z)                 # četnosti
## z
##  1  2  3  4  5  6 
## 36 30 39 32 33 30
table(factor(z))         # četnosti
## 
##  1  2  3  4  5  6 
## 36 30 39 32 33 30
summary(z)               # chová se k číslům jako numeric, tedy popisné statistiky
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    2.00    3.00    3.43    5.00    6.00
summary(factor(z))       # četnosti
##  1  2  3  4  5  6 
## 36 30 39 32 33 30

Jedna z výhod Rka je jeho přímočaré a přehledné použití statistických testů:

t.test(x, mu = 5)        # Jednovýběrový t-test
## 
##  One Sample t-test
## 
## data:  x
## t = -0.3902, df = 199, p-value = 0.6968
## alternative hypothesis: true mean is not equal to 5
## 95 percent confidence interval:
##  4.475906 5.350945
## sample estimates:
## mean of x 
##  4.913426
t.test(x, y)             # Dvouvýběrový t-test
## 
##  Welch Two Sample t-test
## 
## data:  x and y
## t = -1.501, df = 386.86, p-value = 0.1342
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.0058805  0.1349366
## sample estimates:
## mean of x mean of y 
##  4.913426  5.348898
var.test(x, y)           # Test o shodě rozptylů
## 
##  F test to compare two variances
## 
## data:  x and y
## F = 1.4088, num df = 199, denom df = 199, p-value = 0.01602
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  1.066147 1.861530
## sample estimates:
## ratio of variances 
##           1.408781
wilcox.test(x, y)        # Wilcoxonův dvouvýběrový test
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  x and y
## W = 18185, p-value = 0.1165
## alternative hypothesis: true location shift is not equal to 0
cor.test(x, y)           # Korelační test
## 
##  Pearson's product-moment correlation
## 
## data:  x and y
## t = 0.10245, df = 198, p-value = 0.9185
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.1315932  0.1458744
## sample estimates:
##         cor 
## 0.007280715
chisq.test(table(z, w))  # Chí-kvadrát test nezávislosti
## 
##  Pearson's Chi-squared test
## 
## data:  table(z, w)
## X-squared = 2.2286, df = 5, p-value = 0.8167
lm(x ~ z)                # Lineární regrese
## 
## Call:
## lm(formula = x ~ z)
## 
## Coefficients:
## (Intercept)            z  
##     5.06962     -0.04554
anova(lm(x ~ z))         # ANOVA
## Analysis of Variance Table
## 
## Response: x
##            Df  Sum Sq Mean Sq F value Pr(>F)
## z           1    1.18  1.1841  0.1197 0.7297
## Residuals 198 1958.04  9.8891

Zde si o detailech testů a jejich správném použití nebudeme nic vykládat. K tomu jsou určeny příslušné statistické kurzy.

Úložky na procvičení

Vyřešte si to sami, aniž byste se dívali do řešení (úplně dole vespod skriptu).

  1. Předpokládejte, že máte k dispozici jen funkci runif pro generování z rovnoměrného rozdělení na (0,1). Naprogramujte si svou vlastní verzi funkce sample(, replace = TRUE, prob), tedy generování z diskrétního rozdělení na daných hodnotách s danými pravděpodobnostmi. Zkuste i pro nějaké spojité rozdělení, třeba normální rozdělení (využijte vhodné transformace).

  2. Byli jste loterijní společností požádáni, abyste vylosovali 1 tah čísel loterie na tento týden. Losuje se 6 z 49 čísel.

  3. Uvažme pravděpodobnostní rozdělení na množině \(\{0, 1, ..., n\}\) definované tak, že \(\mathsf{P}(X = 0) = p \in (0,1)\) a \(\mathsf{P}(X = i) = \mathsf{P}(X = j)\) pro každé \(i, j \in \{1, ..., n\}\). Nagenerujte náhodný výběr z tohoto rozdělení o rozsahu 5000 a napočtěte relativní četnosti.

  4. Nagenerujte 100 výběrů o rozsahu 50 z diskrétního rozdělení na množině \(\{1,2,3\}\) s pravděpodobnostmi \(p_1 = p_2 = 0.2\) a \(p_3 = 0.6\). Spočtěte průměrné relativní četnosti napříč všemi výběry.

  5. Čerstvý absolvent vysoké školy se stěhuje do Houstonu v Texasu, aby nastoupil do nového zaměstnání, a hledá si dům ke koupi. Vzhledem k tomu, že metropolitní oblast Greater Houston zahrnuje relativně velké území s téměř 7 000 000 obyvateli, je zde mnoho domů, z nichž si lze vybrat. Při prohlížení realitních webových stránek je možné vybrat cenové rozpětí nemovitostí, o které má člověk největší zájem. Předpokládejme, že potenciální kupující zadá cenu 200 000 až 250 000 dolarů a výsledkem je 105 domů s cenami rovnoměrně rozloženými v tomto rozmezí.

  1. Předpokládejme, že výsledky testů na vysoké škole odpovídají normálnímu rozložení. Průměrný výsledek testu je 72 a směrodatná odchylka je 15,2. Určete procentuální podíl studentů, kteří v testu dosáhli 84 nebo více bodů.

  2. Předpokládejme, že IQ má normální rozložení s průměrem 100 a směrodatnou odchylkou 15.

  1. Podle britských meteorologů je průměrný měsíční úhrn srážek v Londýně v měsíci červnu µ = 2,09 palce. Předpokládejme, že měsíční úhrn srážek je normálně rozložená náhodná veličina se směrodatnou odchylkou σ = 0,48 palce.
  1. Čas potřebný studentům zapsaným do předmedicínského programu k dokončení závěrečné zkoušky z organické chemie je normálně rozložen s průměrem µ = 200 minut a směrodatnou odchylkou σ = 20 minut.

  1. Předpokládejme, že průměrná doba odbavení pokladníkem v supermarketu je 3 minuty. Určete pravděpodobnost, že pokladník odbaví zákazníka za méně než 2 minuty. (Použijte exponenciální rozdělení, dbejte na to, jak je definováno v R.)

  2. Předpokládejme, že v testu z angličtiny je 12 otázek a každá otázka má 5 možných odpovědí, z nichž pouze jedna je správná. Určete:

  1. Vytvořte vektor s 10 nezávislými realizacemi (10 hodnotami) náhodné veličiny, která představuje počet úspěchů v 5 (nezávislých) pokusech s 80% pravděpodobností úspěchu.

  1. Vytvořte náhodný vektor 100 náhodných čísel z rovnoměrného rozdělení v intervalu (100, 150). Předpokládejme, že tento vektor symbolizuje nějaká naměřená data, ale s 10% pravděpodobností obsahují nějakou velkou systematickou chybu měření. Předpokládejme, že tato systematická chyba měření je nějaká náhodná proměnná z normálního rozdělení s průměrem 1000 a směrodatnou odchylkou 200. Přičtěte tyto chyby měření příslušným pozorováním a zakreslete do grafu (plot, hist, boxplot).

  2. Na základě známé studie bylo zjištěno, že 90 % populace si čistí zuby jednou denně. Odpovězte na následující otázky pro vzorek 20 osob:

  1. Je známo, že 5 % všech daňových přiznání obsahuje alespoň jednu chybu. Jaká je pravděpodobnost, že z náhodného vzorku 10 daňových přiznání budou chyby obsahovat nejvýše 2 z nich?

  2. Pokud v průměru za minutu přejede most 12 aut, určete následující:

  1. DVD má v průměru jednu vadu na každé 2 palce podél své dráhy. Jaká je pravděpodobnost, že v úseku o délce 5 palců bude méně než 3 vady?

  2. Najděte 2.5% a 97.5% kvantily Studentova t-rozdělení o 5 stupních volnosti. Srovnejte se stejnými kvantily standardního normálního rozdělení.

  3. Počet zaměstnanců pro přijímání hovorů ve společnosti je založen na předpokladu, že bude přijato 180 telefonních hovorů za hodinu, které budou náhodně rozloženy. Pokud je v období 5 minut přijato 20 nebo více hovorů, kapacita je překročena a dojde k nežádoucí čekací době, proto je kapacita stanovena na 19 hovorů za 5 minut. Jaká je pravděpodobnost, že bude kapacita překročena v náhodně zvoleném období 5 minut?

  4. Intervalové odhady. Uvažte náhodný výběr \(X_1\), …, \(X_n\) z normálního rozdělení se střední hodnotou \(\pi\) a směrodatnou odchylkou 1. Zkonstruujte 95% interval spolehlivosti pro střední hodnotu následujícího tvaru: \[ \mathsf{P}\left(\overline{X}_n - t_{n-1}(0.975) \frac{\widehat{\sigma}_n}{\sqrt{n}} < \mu < \overline{X}_n + t_{n-1}(0.975) \frac{\widehat{\sigma}_n}{\sqrt{n}} \right) = 0.95, \] kde \(\overline{X}_n\) je výběrový průměr, \(\widehat{\sigma}_n\) je výběrová směrodatná odchylka a \(t_{m}(\alpha)\) značí \(\alpha\)-kvantil Studentova t-rozdělení o \(m\) stupních volnosti.