Příklad 4
Je dána kružnice \(k\) a bod \(X\) ležící v její vnitřní oblasti. Sestrojte všechny rovnoramenné lichoběžníky \(ABCD\) vepsané kružnici \(k\) tak, aby střed \(S\) kružnice \(k\) ležel na základně \(AB\), bod \(X\) ležel na základně \(CD\) a aby platilo \(|DX|:|CX|=1:3\).
Rozbor
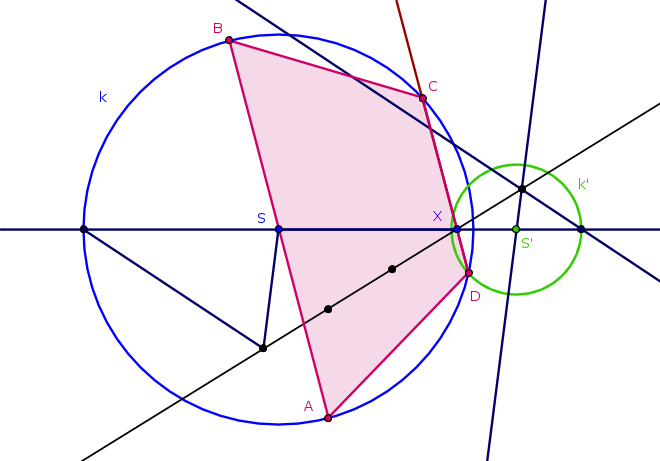
Obr. 4.1.3 - Náčrtek příkladu 4
- Nejprve zkonstruujeme základnu \(CD\). Pro ni má platit \(|DX|=\frac{1}{3}|CX|\), přitom bod \(D\) má ležet na polopřímce opačné k polopřímce \(XC\). Proto je bod \(D\) obrazem bodu \(C\) ve stejnolehlosti se středem v bodě \(X\) a koeficientem \(-\frac{1}{3}\).
- Bod \(C\) leží na kružnici \(k\), bod \(D\) proto leží na obrazu \(k'\) kružnice \(k\) ve stejné stejnolehlosti.
Pro ty z vás, kdo si nejste jistí, jak se zjistí střed kružnice \(k'\) a její poloměr, jsou hlavní myšlenky konstrukce připomenuty zde: 
Applet 4.1.8
- Bod \(D\) je průsečík kružnic \(k\), \(k'\), bod \(C\) je průsečík kružnice \(k\) a polopřímky \(DX\).
- Body \(A\), \(B\) pak získáme z rovnoběžnosti základen lichoběžníka.
Konstrukce a zápis konstrukce
Applet 4.1.6 - Příklad 4
Diskuse
- Úloha nemá řešení, pokud bod \(X\) leží ve vnější oblasti kružnice \(l\), která je soustředná s kružnicí \(k\) a má poloviční poloměr.
- Úloha má jinak 2 řešení.
Další příklady
| Příklad 1 | Příklad 2 | Příklad 3 | Příklad 4 | Příklad 5 |
