Příklad 2
Je dán čtverec \(ABCD\). Sestrojte čtverec \(A'B'C'D'\) tak, aby pro obsahy čtverců platilo \(S_{ABCD}:S_{A'B'C'D'}=4:9\), aby bod \(A'=A\) a bod \(C\) ležel na úhlopříčce \(A'C'\).
Rozbor
Označme si \(a\) stranu čtverce \(ABCD\), \(b\) stranu čtverce \(A'B'C'D'\).
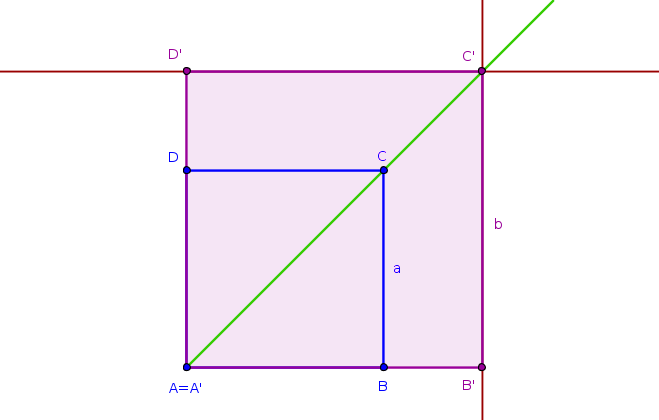
Obr. 4.1.1 - Náčrtek příkladu 2
- Má platit \(S_{ABCD}:S_{A'B'C'D'}=4:9\) neboli \(S_{ABCD}= \frac{4}{9}S_{A'B'C'D'}\). Tedy pro strany čtverců má platit vztah \(a^2=\frac{4}{9}b^2\), tj. \(b=\frac{3}{2}a\).
- Víme, že bod \(A'=A\) a že bod \(C\) leží na úhlopříčce \(A'C'=AC'\). Proto musí bod \(C'\) ležet na polopřímce \(AC\).
- Protože jsou čtverce \(ABCD\), \(A'B'C'D'\) podobné, bude platit \(|AB|:|A'B'|=|AC|:|A'C'|=2:3\). Body \(B'\), \(C'\), \(D'\) jsou tedy obrazy bodů \(B\), \(C\), \(D\) ve stejnolehlosti určené středem \(A\) a koeficientem \(\frac{3}{2}\).
- Body \(B'\), \(D'\) jsou obrazy bodů \(B\), \(D\) v dané stejnolehlosti a z vlastností stejnolehlosti plyne, že bod \(C'\) leží na příslušných rovnoběžkách se stranami čtverce \(ABCD\) (obr. 4.1.1).
- Platí: \(\frac{3}{2}|AD| = |AD|+\frac{1}{2}|AD|\), polovinu délky strany \(AD\) získáme tak, že najdeme její střed. Chceme-li získat bod \(D'\) jako obraz bodu \(D\) ve stejnolehlosti se středem \(A\) a koeficientem \(\frac{3}{2}\), stačí na polopřímku opačnou k \(DA\) vynést polovinu strany \(AD\).
Konstrukce a zápis konstrukce
Applet 4.1.4 - Příklad 2
Závěr
Úloha má jedno řešení.
Další příklady
| Příklad 1 | Příklad 2 | Příklad 3 | Příklad 4 | Příklad 5 |
