We investigate certain envelopes of open sets in dual Banach spaces which are related to extending holomorphic functions. We give a variety of examples of absolutely convex sets showing that the extension is in many cases not possible. We also establish connections to the study of iterated weak* sequential closures of convex sets in the duals of separable spaces.
We provide a corrected proof of Theorem 9 in [D.A. Edwards, Systèmes projectifs d'ensembles convexes compacts, Bulletin de la S.M.F. 103 (1975), 225-240] stating that any metrizable infinite-dimensional simplex is affinely homeomorphic to the intersection of a decreasing sequence of Bauer simplices.
We study linearly ordered spaces which are Valdivia compact in their order topology. We find an internal characterization of these spaces and we present a counterexample disproving a conjecture posed earlier by the first author. The conjecture asserted that a compact line is Valdivia compact if its weight does not exceed
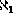 ,
every point of uncountable character is isolated from one side and every closed
first countable subspace is metrizable. It turns out that the
last condition is not sufficient. On the other hand, we show that
the conjecture is valid if the closure of the set of points of
uncountable character is scattered. This improves an earlier
result of the first author.
,
every point of uncountable character is isolated from one side and every closed
first countable subspace is metrizable. It turns out that the
last condition is not sufficient. On the other hand, we show that
the conjecture is valid if the closure of the set of points of
uncountable character is scattered. This improves an earlier
result of the first author.
If X is a compact convex set in a real locally convex space, a subset B of X is said to be its boundary if every affine continuous function on X attains its maximum at some point of B. We study relations between fragmentability of B and the whole set X and a connection of this question to the boundary problem. As a byproduct we obtain a characterization of separable Asplund spaces. We further prove the positive answer to the boundary problem under some topological assumptions on the boundary. We also study the possibility of finding the Haar system in a boundary of a metrizable compact convex set.
We collect examples of Valdivia compact spaces, their continuous images and associated classes of Banach spaces which appear naturally in various branches of mathematics. We focus on topological constructions generating Valdivia compact spaces, linearly ordered compact spaces, compact groups, L1 spaces, Banach lattices and non-commutative L1 spaces.
On each nonreflexive Banach space X there exists a positive continuous convex function f such that 1/f is not a d.c. function (i.e., a difference of two continuous convex functions). This result together with known ones implies that X is reflexive if and only if each everywhere defined quotient of two continuous convex functions is a d.c. function. Our construction gives also a stronger version of Klee's result concerning renormings of nonreflexive spaces and non-norm-attaining functionals.
We investigate the question which compact convex sets are homeomorphic to their product with the unit interval. We prove it in particular for the space of probability measures on any infinite scattered compact space and for the half-ball of a nonseparable Hilbert space equipped with the weak topology. We also show examples of compact spaces for which it is not the case.
We study an order relation on the fibers of a continuous map and its application to the study of the structure of compact spaces of uncountable weight.
We study the (I)-envelopes of the unit balls of Banach spaces. We show, in particular, that any nonreflexive space can be renormed such that the (I)-envelope of the unit ball is not the whole bidual unit ball. Further, we give a simpler proof of the James' characterization of reflexivity in nonseparable case. We also study the spaces in which the (I)-envelope of the unit ball adds nothing.
A convergence structure generalizing the order convergence structure on the set of Hausdorff continuous interval functions is defined on the set of minimal usco maps. The properties of the obtained convergence space are investigated and essential links with the pointwise convergence and the order convergence are revealed. The convergence structure can be extended to a uniform convergence structure so that the convergence space is complete. The important issue of the denseness of the subset of all continuous functions is also addressed.
We investigate Baire-one functions whose graph is contained in a graph of usco mapping. We prove in particular that such a function defined on a metric space with values in Rd is the pointwise limit of a sequence of continuous functions with graphs contained in the graph of a common usco map.
We study the notion of (I)-generating introduced by V. Fonf and J. Lindendstrauss and a related notion of (I)-envelope. As a consequence of our results we get an easy proof of the James characterization of weak compactness in Banach spaces with weak* angelic dual unit ball and an easy proof of the James characterization of reflexivity within a large class of spaces. We also show by an example that the general James theorem cannot be proved by this method.
We show that a complex Banach space is weakly Lindelöf determined if and only if the dual unit ball of any equivalent norm is weak* Valdivia compactum. We deduce that a complex Banach space X is weakly Lindelöf determined if and only if any nonseparable Banach space isomorphic to a complemented subspace of X admits a projectional resolution of the identity. These results complete the previous ones on real spaces.
We study the classes of complex Banach spaces with Valdivia dual unit ball. We give complex analogues of several theorems of real spaces. Further we study relationship of these complex Banach spaces with their real versions and that of real Banach spaces and their complexification. We also formulate several open problems.
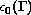
We give two examples of scattered compact spaces K such that C(K) is not uniformly homeomorphic to any subset of
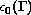 for any set
for any set
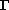 .
The first one is
.
The first one is
![$[0,\omega_1]$](obr/0om1.gif) and hence it has the smallest
possible cardinality,
the other one has the smallest possible height
and hence it has the smallest
possible cardinality,
the other one has the smallest possible height
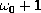 .
.
(Foreword:We present two results of Jan Pelant. He presented them at seminars in the Mathematical Institute of Czech Academy of Sciences during last two years. The example described in Theorem 4.1 below is quite recent. Unfortunately, Jan Pelant died before the results were prepared for publication. We decided to reconstruct them using his hand-written notes. )
Let X be a compact convex subset of a locally convex space. We show that any bounded Baire-one function defined on ext X can be extended to an affine Baire-one function on X if and only if X is a Choquet simplex and ext X satisfies a certain topological property.
We study the possibility of extending any bounded Baire-one function on the set of extreme points of a compact convex set to an affine Baire-one function and related questions. We give complete solutions to these questions within a class of Choquet simplicies introduced by P.J.Stacey (1979). In particular we get an example of a Choquet simplex such that its set of extreme points is not Borel but any bounded Baire-one function on the set of extreme points can be extended to an affine Baire-one function. We also study the analogous questions for functions of higher Baire classes.
We investigate the possibility of extension of Baire-one functions from subspaces of topological spaces. In particular we prove that any Baire-one function on a Lindelöf hereditarily Baire completely regular space can be extended to a Baire-one function on any completely regular superspace.
We show that a compact space K has a dense set of
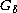 points if it can be covered by countably many Corson countably
compact spaces. If these Corson countably compact spaces may be
chosen to be dense in K, then K is even Corson.
points if it can be covered by countably many Corson countably
compact spaces. If these Corson countably compact spaces may be
chosen to be dense in K, then K is even Corson.
Topological spaces of signed Radon measures on a Tychonoff space X inherit some descriptive properties of the space X. We show in particular that the space of signed Radon measures on an absolute Borel (Cech-analytic) space is again absolute Borel (Cech-analytic). Main tool in proving such results is study of measurability of evaluation functions.
If X is an infinite-dimensional Banach space, with separable dual, and
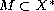 is an analytic set such that any point
is an analytic set such that any point
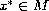 can be reached from 0 by a continuous path contained
(except for the point x*) in the interior of
M, then M is the
range of the derivative of a C1-smooth function on
X with bounded nonempty support.
can be reached from 0 by a continuous path contained
(except for the point x*) in the interior of
M, then M is the
range of the derivative of a C1-smooth function on
X with bounded nonempty support.
We study properties of the class of continuous images of Valdivia compact spaces. We introduce its subclass (weakly Corson compact spaces) which is closed to taking subspaces. Further we investigate Banach spaces with dual unit ball being a continuous image of a Valdivia compactum or weakly Corson and establish several stability and non-stability properties.
Assuming the consistency of the existence of a measurable cardinal, it is consistent to have two Banach spaces, X,Y, where X is a weak Asplund space such that X* (in the weak* topology) in not in Stegall's class, whereas Y* is in Stegall's class but is not weak* fragmentable.
We show that, under some additional set-theoretical assumptions which are equiconsistent with the existence of a measurable cardinal, there is a weak Asplund space whose dual equipped with the weak* topology is not in the Stegall class. This completes a result by Kenderov, Moors and Sciffer.
We prove in particular that the space
![$C[0,\omega_2]$](obr/c0om2.gif) has no countably norming Markushevich basis. This answers a question asked by
G.Alexandrov and A.Plichko.
has no countably norming Markushevich basis. This answers a question asked by
G.Alexandrov and A.Plichko.
We give an example of a Banach space which admits no projectional resolution of the identity but whose dual unit ball in weak* topology is a Valdivia compact. This answers a question asked by M.Fabian, G.Godefroy and V.Zizler.
Let us call a Banach space Plichko (1-Plichko) if it admits a countably norming (countably 1-norming) Markushevich basis. We introduce a subclass of Plichko spaces strictly containing weakly Lindelöf determined spaces which is stable to isomorphisms, subspaces and quotients. Further we prove that each quotient of the space
![$C[0,\omega_1]$](obr/com1.gif) is 1-Plichko.
is 1-Plichko.
We prove that a Banach space X is weakly Lindelöf determined if (and only if) each non-separable Banach space isomorphic to a complemented subspace of X has a projectional resolution of the identity. This answers a question posed by S.Mercourakis and S.Negrepontis and yields a converse of Amir-Lindenstrauss'theorem. We also prove that a Banach space of the form C(K)where K is a continuous image of a Valdivia compactum is weakly Lindelöf determined if (and only if) each non-separable Banach space isometric to a subspace of C(K) has a projectional resolution of the identity.
We characterize topological spaces which have a subset with non-closed double-derived set. As a corollary we obtain that the double-derived set of an arbitrary subset of a
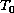 topological space is closed.
This answers in the negative a question asked by A.Lelek in
Houston Problem Book (1995).
topological space is closed.
This answers in the negative a question asked by A.Lelek in
Houston Problem Book (1995).
We give an example of an Asplund space -
![$C[0,\omega_2]$](obr/c0om2.gif) with an
equivalent norm - whose bidual unit ball is not a Valdivia compact.
This answers in the negative a question of J.Orihuela (1992).
Further we introduce a subclass of Asplund spaces, which has nice
stability properties and each element of which has Valdivia bidual unit ball.
This class contains all Asplund spaces whose dual unit ball is
with an
equivalent norm - whose bidual unit ball is not a Valdivia compact.
This answers in the negative a question of J.Orihuela (1992).
Further we introduce a subclass of Asplund spaces, which has nice
stability properties and each element of which has Valdivia bidual unit ball.
This class contains all Asplund spaces whose dual unit ball is
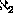 -Corson
(in particular, all Asplund spaces of density
-Corson
(in particular, all Asplund spaces of density
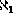 and all Asplund weakly compactly generated spaces).
and all Asplund weakly compactly generated spaces).
We prove in particular that the dual unit ball of a Banach space
X is a Corson compact provided X is of the form
C(K) where K is a continuous image of a
Valdivia compact space, and the dual unit ball of every subspace of
X is Valdivia compact. Another result is that, if
K is a non-Corson continuous image of a Valdivia compact,
there is a continuous image L ofK
such that the dual unit ball of C(L) is not Valdivia.
![$[0,\omega_1]$](obr/0om1.gif) into Continuous Images of Valdivia Compacta
into Continuous Images of Valdivia Compacta
We prove in particular that a continuous image of a Valdivia
compact space is Corson provided it contains no homeomorphic copy
of the ordinal segment ![$[0,\omega_1]$](obr/0om1.gif) .
This generalizes a result of R.Deville and G.Godefroy who proved it
for Valdivia compact spaces. We give also a refinement of their result
which yields a pointwise version of retractions on a Valdivia compact space.
.
This generalizes a result of R.Deville and G.Godefroy who proved it
for Valdivia compact spaces. We give also a refinement of their result
which yields a pointwise version of retractions on a Valdivia compact space.
We prove that the dual unit ball of a Banach space Xis a
Corson compact provided that the dual unit ball with respect to every
equivalent norm on X is a Valdivia compact. As a corollary we
get that the dual unit ball of a Banach space X of density
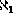 is Corson if
X has projectional resolution of the identity with respect to
every equivalent norm. These results answer questions posed by M.Fabian,
G.Godefroy and V.Zizler.
is Corson if
X has projectional resolution of the identity with respect to
every equivalent norm. These results answer questions posed by M.Fabian,
G.Godefroy and V.Zizler.
We characterize Valdivia compact spaces K in terms of
C(K) endowed with a topology introduced by M.Valdivia (1991).
This generalizes R.Pol's characterization of Corson compact spaces.
Further we study duality, products and open continuous images of Valdivia
compact spaces. We prove in particular that the dual unit ball of
C(K) is Valdivia wheneverK is Valdivia and that
the converse holds whenever K has a dense set of
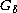 points. Another result is that
any open continuous image of a Valdivia compact space with a dense set of
points. Another result is that
any open continuous image of a Valdivia compact space with a dense set of
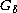 points is again Valdivia.
points is again Valdivia.
We study topological properties of Valdivia compact spaces. We prove in
particular that a compact Hausdorff space K is Corson
provided each continuous image of K is a Valdivia compact.
This answers a question of M.Valdivia (1997). Another results are that the
class of Valdivia compacta is stable with respect to arbitrary products and
a generalization of the fact that Corson compacta are angelic.
We prove that the dual unit ball of the space
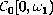 endowed with the weak* topology is not a Valdivia compact. This answers a
question posed to the author by V.Zizler and has several consequences.
Namely, it yields an example of an affine continuous image of a convex
Valdivia compact (in the weak* topology of a dual Banach space) which is not
Valdivia, and shows that the property of the dual unit ball being
Valdivia is not an isomorphic property. Another consequence is that the space
endowed with the weak* topology is not a Valdivia compact. This answers a
question posed to the author by V.Zizler and has several consequences.
Namely, it yields an example of an affine continuous image of a convex
Valdivia compact (in the weak* topology of a dual Banach space) which is not
Valdivia, and shows that the property of the dual unit ball being
Valdivia is not an isomorphic property. Another consequence is that the space
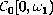 has no countably 1-norming Markusevic basis.
has no countably 1-norming Markusevic basis.
The spaces of Borel probabilities on a topological space X
inherit a number of topological properties of X.
We show in particular that the space of tight probabilities on a Cech-analytic
space is Cech-analytic. Analogical results are shown for several other
classes of generalized analytic and complete topological spaces.
Using modifications of the well-known construction of "double-arrow" space
we give consistent examples of nonfragmentable compact Hausdorff spaces which
belong to Stegall's class . Namely the following
is proved.
(1) If 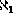 is less than the least inaccessible cardinal in
and
is less than the least inaccessible cardinal in
and
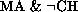 hold then there is a nonfragmentable compact Hausdorff space K
such that every minimal usco mapping of a Baire space intoK
is singlevalued at points of a residual set.
hold then there is a nonfragmentable compact Hausdorff space K
such that every minimal usco mapping of a Baire space intoK
is singlevalued at points of a residual set.
(2) If V=L then there is a nonfragmentable compact Hausdorff
space K such that every minimal usco mapping of a completely
regular Baire space intoK
is singlevalued at points of a residual set.
We introduce a new class of hereditarily t-Baire spaces
(defined by G.Koumoullis (1993)) which need not to have the restricted Baire
property in a compactification - as an example serves the space
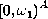 for A uncountable. We use this and a modification of a
construction of D.Fremlin (1987) to get, under the assumption that there is a
measurable cardinal, an example of a first class function of a hereditarily
t-Baire space into a metric space which has no point of continuity, which shows,
in answer to a question of G.Koumoullis (1993), that the cardinality
restriction in his Theorem 4.1 cannot be dropped.
for A uncountable. We use this and a modification of a
construction of D.Fremlin (1987) to get, under the assumption that there is a
measurable cardinal, an example of a first class function of a hereditarily
t-Baire space into a metric space which has no point of continuity, which shows,
in answer to a question of G.Koumoullis (1993), that the cardinality
restriction in his Theorem 4.1 cannot be dropped.
It is shown in particular that the question whether every extended Borel
class one (e.g.
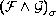 -measurable)
map of any hereditarily Baire space into a metric space has the point of
continuity property is equivalent to the Kuratowski question whether the
function with the Baire property of any topological space into a metric
space is continuous apart from a meager set. The method of the proof
enables us to get, under the assumption that it is consistent to suppose
that there is a measurable cardinal, examples of ordinary Borel class one maps
(i.e.
-measurable)
map of any hereditarily Baire space into a metric space has the point of
continuity property is equivalent to the Kuratowski question whether the
function with the Baire property of any topological space into a metric
space is continuous apart from a meager set. The method of the proof
enables us to get, under the assumption that it is consistent to suppose
that there is a measurable cardinal, examples of ordinary Borel class one maps
(i.e. 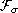 -measurable)
of a hereditarily Baire space intoa metric space which have not the point
of continuity property.These examples complete and strengthen an example of
G.Koumoullis, who constructed (under the assumption that there is a
real-valued measurable cardinal
-measurable)
of a hereditarily Baire space intoa metric space which have not the point
of continuity property.These examples complete and strengthen an example of
G.Koumoullis, who constructed (under the assumption that there is a
real-valued measurable cardinal
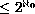 an extended Borel class one function (even
an extended Borel class one function (even
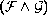 -measurable)
of a hereditarily Baire space into a metric space with no continuity
point but it is not clear whether this map is
-measurable)
of a hereditarily Baire space into a metric space with no continuity
point but it is not clear whether this map is
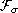 -measurable.
-measurable.
We prove in particular that if X is a hereditarily Baire
space which has the tightness less than the least weakly inaccessible cardinal
and each (closed) subspace of Xhas the countable chain condition,
then every Borel class one map of X into a metric space
M has the point of continuity property. In the case of
countable tightness the assumption that every closed subspace has the
countable chain condition is not needed and we get a result of R.W.Hansell
(1991).
 Envelopes of open sets and extending holomorphic functions on
dual Banach spaces
(with D.Garcia and M.Maestre; Preprint no.
MATH-KMA-2009/306, see
KMA
Preprint
Series; http://arxiv.org/abs/0905.2531)
Envelopes of open sets and extending holomorphic functions on
dual Banach spaces
(with D.Garcia and M.Maestre; Preprint no.
MATH-KMA-2009/306, see
KMA
Preprint
Series; http://arxiv.org/abs/0905.2531)
 Descriptive hierarchy of complex Banach spaces,
Spring 2005, unpublished manuscript - pdf file (237 kB); Preprint no.
MATH-KMA-2005/169, see
KMA Preprint Series
Descriptive hierarchy of complex Banach spaces,
Spring 2005, unpublished manuscript - pdf file (237 kB); Preprint no.
MATH-KMA-2005/169, see
KMA Preprint Series