The goal of this exercise is to demonstrate the use of packages JM and JMbayes for fitting joint models pursued by JAGS in Exercise 3c. No report is required, just admire the simplicity of the solution (compared to JAGS).

Data and model description

We once again analyze the aids data from library(JM), see help(aids) for more details.

set.seed(123456789)
library(JM)
head(aids[,c("patient", "Time", "death", "CD4", "obstime", "drug", "start", "stop", "event")], 15)
##    patient  Time death       CD4 obstime drug start  stop event
## 1        1 16.97     0 10.677078       0  ddC     0  6.00     0
## 2        1 16.97     0  8.426150       6  ddC     6 12.00     0
## 3        1 16.97     0  9.433981      12  ddC    12 16.97     0
## 4        2 19.00     0  6.324555       0  ddI     0  6.00     0
## 5        2 19.00     0  8.124038       6  ddI     6 12.00     0
## 6        2 19.00     0  4.582576      12  ddI    12 18.00     0
## 7        2 19.00     0  5.000000      18  ddI    18 19.00     0
## 8        3 18.53     1  3.464102       0  ddI     0  2.00     0
## 9        3 18.53     1  3.605551       2  ddI     2  6.00     0
## 10       3 18.53     1  6.164414       6  ddI     6 18.53     1
## 11       4 12.70     0  3.872983       0  ddC     0  2.00     0
## 12       4 12.70     0  4.582576       2  ddC     2  6.00     0
## 13       4 12.70     0  2.645751       6  ddC     6 12.00     0
## 14       4 12.70     0  1.732051      12  ddC    12 12.70     0
## 15       5 15.13     0  7.280110       0  ddI     0  2.00     0

Let us recall the model we were able to fit with JAGS in Exercise 3c. For CD4 variable, we assume LME model with random intercept and slope:

According to this model, the expected CD4 cell count \(m_i(t)\) evolves linearly with time for each patient differently \(m_i(t) = B_{1i} + B_{2i} t\). This will monotonously project into the survival probability of each patient.

Many patients leave the study prior their death, which leads to right-censored data. The observed data are event times \(E_i = \min\{T_i, C_i\}\) and \(\delta_i = \mathbf{1} (T_i \leq C_i)\) where \(C_i\) is assumed to be time of censoring, independent of \(T_i\).
The distribution of time to death \(T_i\) for patient \(i\) is modelled through the hazard function: \[\begin{align*} h_i(t) &= h_0(t) \, \exp\left\{ \gamma_1 D_i + \gamma_2 m_i(t) \right\} \\ &= h_0(t) \, \exp\left\{ \gamma_1 D_i + \gamma_2 B_{1i} + t \cdot \gamma_2 B_{2i} \right\}, \end{align*}\] where we were able to implement only constant \(h_0(t) = \xi\) or piecewise constant baseline hazard function \(h_0(t) = \prod\limits_{k=1}^{K} \xi_k^{\mathbf{1}(t_k < t \leq t_{k+1})}\). The constant baseline hazard yields Gompertz distribution with monotonous hazard function in time. The piecewise constant baseline can adjust the monotonous exponential trend, but cannot fully reverse the monotonicity for an interval.

According to smoothed derivative of Breslow estimator of cumulative hazard function from classical semi-parametric Cox proportional hazards model, the shape should resemble the following shape: Such a shape calls for an even more flexible baseline hazard parametrizations such as B-splines on log-scale. However, we will no longer be able to find the closed formula for cumulative hazard \(H_i(t)\).

The likelihood function for observed data (in the general notation defined below) is of the following form: \[ p(\mathbb{Y}, \mathbf{E}, \boldsymbol{\delta} \,|\, \boldsymbol{\beta}, \sigma^2, \mathbb{D}, \boldsymbol{\gamma}, \alpha, \boldsymbol{\xi} \text{ or } \boldsymbol{\gamma}_{h_0}) = \\ = \prod\limits_{i=1}^n \int p(\mathbf{Y}_i | \mathbf{B}_i; \boldsymbol{\beta}, \sigma^2) \, \left[h_i(E_i | \mathbf{B}_i; \boldsymbol{\gamma}, \alpha, \boldsymbol{\xi} \text{ or } \boldsymbol{\gamma}_{h_0})\right]^{\delta_i} \, \exp\{-H_i(E_i | \mathbf{B}_i; \boldsymbol{\gamma}, \alpha, \boldsymbol{\xi} \text{ or } \boldsymbol{\gamma}_{h_0})\} \, p(\mathbf{B}_i | \mathbb{D}) \, \mathrm{d} \mathbf{B}_i \] where the individual contribution to log-likelihood is very complicated integral wrt random effects. For example, when B-spline basis is chosen for the log-baseline hazard, we obtain: \[ \ell(\mathbf{Y}_i, E_i, \delta_i \,|\, \boldsymbol{\beta}, \sigma^2, \mathbb{D}, \boldsymbol{\gamma}, \alpha, \boldsymbol{\gamma}_{h_0} ) = \\ = \log \left\langle\int \exp\left\{ \sum\limits_{j=1}^{n_i} \log p(Y_{ij} \mathbf{B}_i; \boldsymbol{\beta}, \sigma^2) + \delta_i \log h_i(E_i | \mathbf{B}_i; \boldsymbol{\gamma}, \alpha, \boldsymbol{\gamma}_{h_0}) - H_i(E_i | \mathbf{B}_i; \boldsymbol{\gamma}, \alpha, \boldsymbol{\gamma}_{h_0}) + \log p(\mathbf{B}_i | \mathbb{D}) \right\} \, \mathrm{d} \mathbf{B}_i \right\rangle = \\ = \log \left\langle \int \exp\left\{ -\frac{n_i}{2} \log (2\pi\sigma^2) - \frac{1}{2\sigma^2} \sum\limits_{j=1}^{n_i} \left[Y_{ij} - \mathbf{X}_i(t_{ij})^\top \boldsymbol{\beta} - \mathbf{Z}_i(t_{ij})^\top \mathbf{B}_i\right]^2 + \right. \right.\\ \left. + \delta_i \left[ \sum\limits_{q=1}^Q \gamma_{h_0,q} B_q^{\mathsf{spl}}(E_i;\mathbf{v}) + \mathbb{W}_i^\top \boldsymbol{\gamma} + \alpha \left( \mathbf{X}_i(E_i)^\top \boldsymbol{\beta} + \mathbf{Z}_i(E_i)^\top \mathbf{B}_i \right) \right] - \right. \\ \left. - \int\limits_0^{E_i} \exp \left[ \sum\limits_{q=1}^Q \gamma_{h_0,q} B_q^{\mathsf{spl}}(s;\mathbf{v}) + \mathbb{W}_i^\top \boldsymbol{\gamma} + \alpha \left( \mathbf{X}_i(s)^\top \boldsymbol{\beta} + \mathbf{Z}_i(s)^\top \mathbf{B}_i \right) \right] \, \mathrm{d} s - \right. \\ \left. \left. - \frac{1}{2} \log|\mathbb{D}| - \frac{1}{2} \mathbf{B}_i^{\top} \mathbb{D}^{-1} \mathbf{B}_i \right\} \, \mathrm{d} \mathbf{B}_i \right\rangle \] Hence, we need to resort to different R package(s) built for this exact purpose.

Joint model using libraries JM and JMbayes

JM in the name of these packages stands for Joint Models. The two packages estimate the joint models in two different approaches:

The usage of these two packages is straightforward combination of nlme and coxph objects.

The longitudinal outcome of patient \(i\) at time \(t\) is in general assumed to follow traditional LME structure: \[ Y_i(t) = m_i(t) + \varepsilon_i(t) = \mathbf{X}_i(t)^\top \boldsymbol{\beta} + \mathbf{Z}_i(t)^\top \mathbf{B}_i + \varepsilon_i(t), \] where \(\mathbf{B}_i \sim \mathsf{N}_d(\mathbf{0}, \mathbb{D})\) are random effects and \(\varepsilon_i(t) \sim \mathsf{N}(0, \sigma^2)\) is the error term. The data is expected to be given in long format (each visit on separate row). In particular, for aids data set we fit:

lmeFit <- lme(CD4 ~ obstime + obstime:drug,
              random = ~ obstime | patient, data = aids)

The relative risk model for survival model has the shape of \[ h_i(t; \mathcal{M}_i(t)) = h_0(t) \exp \left\{ \mathbf{W}_i^\top \boldsymbol{\gamma} + \alpha m_i(t) \right\}, \] where \(\mathbf{W}_i\) are covariates with fixed values in time, \(\mathcal{M}_i(t) = \left\{m_i(s), 0 \leq s < t \right\}\) is the longitudinal history and \(\alpha\) quantifies the strength of the association between the marker and the risk for an event. For defining the coxph object you have to be aware of the following requirements:

For aids data there also exists the short format of the data aids.id containing only first rows:

coxFit <- coxph(Surv(Time, death) ~ drug, data = aids.id, x = TRUE)

The models are simply joined by jointModel() (from JM) or jointModelBayes() (from JMbayes). They only require the name of the time variable in the mixed effects model and specification of the parametrization and approximation method.

MLE approach

The MLE approach is specified through method argument:

jointFit <- jointModel(lmeFit, coxFit, timeVar = "obstime", method = "piecewise-PH-aGH")
jointFit
## 
## Call:
## jointModel(lmeObject = lmeFit, survObject = coxFit, timeVar = "obstime", 
##     method = "piecewise-PH-aGH")
## 
## Variance Components:
## $`Random-Effects`
##              StdDev    Corr
## (Intercept)  4.5839        
## obstime      0.1822 -0.0468
## 
## $Residual
## Longitudinal 
##       1.7377 
## 
## 
## Coefficients:
## $`Longitudinal Process`
##     (Intercept)         obstime obstime:drugddI 
##          7.2203         -0.1917          0.0116 
## 
## $`Event Process`
## drugddI  Assoct    xi.1    xi.2    xi.3    xi.4    xi.5    xi.6    xi.7 
##  0.3348 -0.2875  0.0786  0.1031  0.1415  0.0820  0.0894  0.0906  0.0886 
## 
## 
## log-Lik: -4328.261

The method syntax follows the format <baseline hazard>-<parameterization>-<numerical integration>. The implemented combinations are:

  • "piecewise-PH-GH": PH model with piecewise-constant baseline hazard: \(\prod\limits_{q=1}^{Q} \xi_q^{\mathbf{1}(v_{q-1} < t \leq v_q)}\), where \(0 = v_0 < v_1 < \cdots < v_Q\) split the time scale,
  • "spline-PH-GH": PH model with B-spline-approximated log baseline hazard: \(\log h_0(t) = \sum\limits_{q=1}^{Q} \gamma_{h_0,q} B_q^{\mathsf{spl}}(t;\mathbf{v})\), where \(B_q^{\mathsf{spl}}(t;\mathbf{v})\) denotes the q-th basis function of a B-spline with knots \(\mathbf{v}\),
  • "weibull-PH-GH": PH model with Weibull baseline hazard,
  • "weibull-AFT-GH": AFT model with Weibull baseline hazard,
  • "Cox-PH-GH": PH model with unspecified baseline hazard,

GH stands for standard Gauss-Hermite; using aGH invokes the pseudo-adaptive Gauss-Hermite rule. Hence, the presented summary should correspond to the model we tried to implement in BONUS Task of Exercise 3c. Compare your estimates with your results to confirm that your implementation yields comparable results.

The control list contains many approximation and implementation details. For example, knots is a numerical vector of the knots positions for the piecewise constant baseline hazard or B-spline log-baseline hazard. In help(jointModel) you can read about the default knot choice by ObsTimes.knots, which corresponds to

(breaks <- c(0, quantile(aids.id$Time, probs = seq(0,1,length.out = 8))[-1]))
##           14.28571% 28.57143% 42.85714% 57.14286% 71.42857% 85.71429%      100% 
##  0.000000  6.227143 11.078571 12.530000 13.930000 15.970000 17.800000 21.400000
jointFit$control$knots
## [1]  6.227144 11.078572 12.530001 13.930001 15.970001 17.800001

The resulting object responds to many familiar functions:

summary(jointFit)                   # classical summary table with p-values
## 
## Call:
## jointModel(lmeObject = lmeFit, survObject = coxFit, timeVar = "obstime", 
##     method = "piecewise-PH-aGH")
## 
## Data Descriptives:
## Longitudinal Process     Event Process
## Number of Observations: 1405 Number of Events: 188 (40.3%)
## Number of Groups: 467
## 
## Joint Model Summary:
## Longitudinal Process: Linear mixed-effects model
## Event Process: Relative risk model with piecewise-constant
##      baseline risk function
## Parameterization: Time-dependent 
## 
##    log.Lik      AIC      BIC
##  -4328.261 8688.523 8754.864
## 
## Variance Components:
##              StdDev    Corr
## (Intercept)  4.5839  (Intr)
## obstime      0.1822 -0.0468
## Residual     1.7377        
## 
## Coefficients:
## Longitudinal Process
##                   Value Std.Err z-value p-value
## (Intercept)      7.2203  0.2218 32.5537 <0.0001
## obstime         -0.1917  0.0217 -8.8374 <0.0001
## obstime:drugddI  0.0116  0.0302  0.3834  0.7014
## 
## Event Process
##             Value Std.Err  z-value p-value
## drugddI    0.3348  0.1565   2.1397  0.0324
## Assoct    -0.2875  0.0359  -8.0141 <0.0001
## log(xi.1) -2.5438  0.1913 -13.2953        
## log(xi.2) -2.2722  0.1784 -12.7328        
## log(xi.3) -1.9554  0.2403  -8.1357        
## log(xi.4) -2.5011  0.3412  -7.3297        
## log(xi.5) -2.4152  0.3156  -7.6531        
## log(xi.6) -2.4018  0.4007  -5.9941        
## log(xi.7) -2.4239  0.5301  -4.5725        
## 
## Integration:
## method: (pseudo) adaptive Gauss-Hermite
## quadrature points: 5 
## 
## Optimization:
## Convergence: 0
fixef(jointFit)                     # fixed effects for LME part
##     (Intercept)         obstime obstime:drugddI 
##      7.22033224     -0.19173550      0.01159239
head(coef(jointFit))                # subject-specific coefficients, process = "Longitudinal"
##   (Intercept)    obstime obstime:drugddI
## 1   10.224905 -0.1370855      0.01159239
## 2    7.362973 -0.1515984      0.01159239
## 3    4.874375 -0.1461400      0.01159239
## 4    4.454885 -0.2057119      0.01159239
## 5    8.421907 -0.1346744      0.01159239
## 6    4.197586 -0.2037221      0.01159239
coef(jointFit, "Event")             # survival model coefficients
##    drugddI     Assoct 
##  0.3348287 -0.2874956
confint(jointFit)                   # confidence intervals for regression coefficients
##                         2.5 %        est.      97.5 %
## Y.(Intercept)      6.78561690  7.22033224  7.65504758
## Y.obstime         -0.23425870 -0.19173550 -0.14921231
## Y.obstime:drugddI -0.04766918  0.01159239  0.07085396
## T.drugddI          0.02813014  0.33482873  0.64152731
## T.Assoct          -0.35780698 -0.28749557 -0.21718415
anova(jointFit)                     # also for two models of the same survival parametrizations
## 
## Marginal Wald Tests Table
## 
## Longitudinal Process
##                 Chisq df Pr(>|Chi|)
## obstime      126.3887  2     <1e-04
## drug           0.1470  1     0.7014
## obstime:drug   0.1470  1     0.7014
## 
## Event Process
##          Chisq df Pr(>|Chi|)
## drug    4.5784  1     0.0324
## Assoct 64.2254  1     <1e-04

The plot method for this object returns the following plots

layout(matrix(c(1,1,1,2,2,2,
                3,3,4,4,5,5,
                6,6,7,7,8,8), nrow = 3, byrow = T))
par(mar = c(4,4,2,0.5))
plot(jointFit, which = c(1:5, 8:10))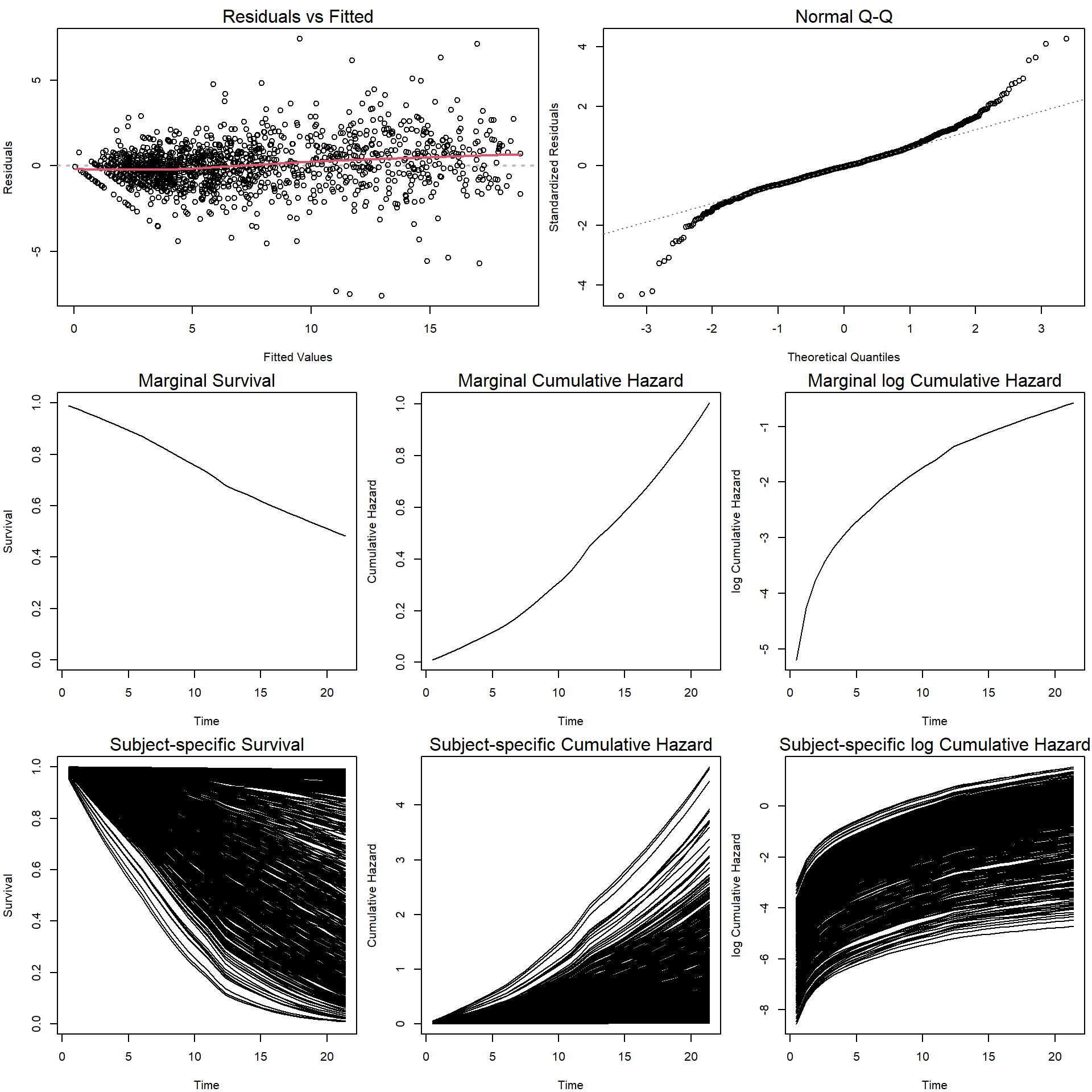

Options which = 6:7 should produce (cumulative) baseline hazard, but they only work with method = "Cox-PH-GH".

par(mfrow = c(1,2))
plot(jointFit, which = 6:7)

But we can plot the estimated baseline hazard on our own. The result should be a piecewise constant function, estimates for which are contained inside jointFit$coefficients$xi.

par(mfrow = c(1,2), mar = c(4,4.1,2,0.5))

# Baseline hazard
plot(0, 0, type = "n", main = "Baseline hazard", 
     xlab = "Time", ylab = expression(Hazard*" "*xi[k]),
     xlim = range(breaks), ylim = c(0, max(jointFit$coefficients$xi)))
segments(x0 = breaks[-length(breaks)], x1 = breaks[-1],
         y0 = jointFit$coefficients$xi, col = "saddlebrown", lwd = 2)

# Cumulative baseline hazard
cumxi <- cumsum(jointFit$coefficients$xi * diff(breaks))
plot(0, 0, type = "n", main = "Cumulative baseline hazard", 
     xlab = "Time", ylab = "Cumulative Hazard",
     xlim = range(breaks), ylim = c(0, max(cumxi)))
abline(v = breaks, col = "grey", lty = 2, lwd = 0.5)
lines(breaks, c(0, cumxi), col = "saddlebrown", lwd = 2)

Function predict predicts values for the longitudinal part of a joint model. By default it predicts the value for 25 equally spaced time points after the last available measurement provided in newdata.

pats <- c(1, 6, 141, 189)
(newdata <- aids[aids$patient %in% pats, ])
##     patient  Time death       CD4 obstime drug gender prevOI         AZT start  stop event
## 1         1 16.97     0 10.677078       0  ddC   male   AIDS intolerance     0  6.00     0
## 2         1 16.97     0  8.426150       6  ddC   male   AIDS intolerance     6 12.00     0
## 3         1 16.97     0  9.433981      12  ddC   male   AIDS intolerance    12 16.97     0
## 19        6  1.90     1  4.582576       0  ddC female   AIDS     failure     0  1.90     1
## 410     141 10.93     1  3.162278       0  ddI   male   AIDS intolerance     0  2.00     0
## 411     141 10.93     1  0.000000       2  ddI   male   AIDS intolerance     2  6.00     0
## 412     141 10.93     1  2.236068       6  ddI   male   AIDS intolerance     6 10.93     1
## 571     189  1.83     0 19.235384       0  ddI   male   AIDS intolerance     0  1.83     0
pred <- predict(jointFit, newdata = newdata, type = "Subject", interval = "prediction", idVar = "patient")
par(mfrow = c(1,length(pats)), mar = c(4,4,2,0.5))
for(i in 1:length(pats)){
  subnd <- newdata[newdata$patient == pats[i],]
  plot(CD4 ~ obstime, data = subnd,  
       xlab = "Time", ylab = "CD4", main = paste("Patient", pats[i]),
       xlim = range(breaks), ylim = c(0, max(pred$upp)),
       col = "royalblue", bg = "skyblue", pch = 21, cex = 1.5)
  lines(attr(pred,"time.to.pred")[[i]], pred$pred[1:25 + (i-1)*25], col = "red", lwd = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$low[1:25 + (i-1)*25], col = "orange", lty = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$upp[1:25 + (i-1)*25], col = "orange", lty = 2)
}

Function survfitJM using Monte Carlo predicts the conditional probability of surviving later times than the last observed time for which a longitudinal measurement was available:

surv <- JM::survfitJM(jointFit, newdata = newdata, idVar = "patient")
par(mfrow = c(1,length(pats)), mar = c(4,4,2,0.5))
plot(surv)

Survival prediction for two patients newly incoming to the study, two different drugs given:

ND <- data.frame(patient = c(1001,1002),
                 obstime = c(0,0),
                 CD4 = c(7,7),                # average CD4 count at obstime == 0
                 drug = factor(c("ddC", "ddI")))
pred <- predict(jointFit, newdata = ND, type = "Subject", interval = "prediction", idVar = "patient")
surv <- JM::survfitJM(jointFit, newdata = ND, idVar = "patient")

par(mfrow = c(1,2), mar = c(4,4,2.5,0.5))
COL <- c("goldenrod", "royalblue")
COLlight <- c("gold", "lightblue")

# Prediction of CD4 evolution
plot(0, 0, type = "n",
     xlim = range(breaks), ylim = c(0, max(pred$upp)),
     xlab = "Time", ylab = "CD4", main = "Longitudinal prediction")
points(0, 7, col = "black", bg = "grey", pch = 21, cex = 1.5)
for(i in 1:2){
  lines(attr(pred,"time.to.pred")[[i]], pred$pred[1:25 + (i-1)*25], col = COL[i], lwd = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$low[1:25 + (i-1)*25], col = COLlight[i], lty = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$upp[1:25 + (i-1)*25], col = COLlight[i], lty = 2)
}
legend("right", levels(ND$drug), bty = "n", title = "Drug", col = COL, lty = 1, lwd = 2)

# Prediction of survival
plot(0, 0, type = "n",
     xlim = range(breaks), ylim = c(0, 1),
     xlab = "Time", ylab = "Survival probability", main = "Survival prediction")
points(0, 1, col = "black", bg = "grey", pch = 21, cex = 1.5)
for(i in 1:2){
  lines(Mean ~ times, data = surv$summaries[[i]], col = COL[i], lwd = 2)
  lines(Lower ~ times, data = surv$summaries[[i]], col = COLlight[i], lty = 2)
  lines(Upper ~ times, data = surv$summaries[[i]], col = COLlight[i], lty = 2)
}
legend("bottomleft", levels(ND$drug), bty = "n", title = "Drug", col = COL, lty = 1, lwd = 2)

Bayesian approach

The Bayesian approach is fitted in a similar way. However, it differs in the parametrization and specification of the baseline hazard. See Details of help(jointModelBayes) to learn what different parametrizations of the effect of the modelled longitudinal outcome are on the hazard with option param. The default choice corresponds to our parametrization above. The log-baseline hazard is modelled only by B-splines (penalized version by prior), see baseHaz option. The knots and order of the spline (ordSpline) are set up in the list control. It also contains adapt, n.iter, n.burnin, n.thin and n.adapt to define the length of Markov chains. The list priors specifies the hyperparameters for prior distributions. The list init contains the initial values for starting the Markov chains.

library(JMbayes)
library(HDInterval)
jointFitB <- jointModelBayes(lmeFit, coxFit, timeVar = "obstime")

Now we examine the contents of this object:

jointFitB
## 
## Call:
## jointModelBayes(lmeObject = lmeFit, survObject = coxFit, timeVar = "obstime")
## 
## Variance Components:
## $`Random-Effects`
##              StdDev    Corr
## (Intercept)  4.5939        
## obstime      0.5741 -0.0289
## 
## $`Residual Std. Err.`
##  sigma 
## 1.7188 
## 
## 
## Coefficients:
## $`Longitudinal Process`
##     (Intercept)         obstime obstime:drugddI 
##          7.1903         -0.2317          0.0088 
## 
## $`Event Process`
##     drugddI      Assoct  Bs.gammas1  Bs.gammas2  Bs.gammas3  Bs.gammas4  Bs.gammas5  Bs.gammas6 
##      0.3296     -0.2965     -2.8036     -2.7127     -2.6391     -2.5823     -2.5386     -2.4965 
##  Bs.gammas7  Bs.gammas8  Bs.gammas9 Bs.gammas10 Bs.gammas11 Bs.gammas12 Bs.gammas13 Bs.gammas14 
##     -2.4516     -2.4133     -2.3871     -2.3891     -2.4101     -2.4401     -2.4748     -2.5083 
## Bs.gammas15 Bs.gammas16 Bs.gammas17 
##     -2.5427     -2.5777     -2.6123 
## 
## 
## DIC: 474139.7
class(jointFitB)                          # JMbayes
## [1] "JMbayes"
jointFitB$priors$priorMean.betas          # hyperparameters of prior distributions
## [1] 0 0 0
jointFitB$control$n.iter                  # total number of iterations sampled
## [1] 20000
jointFitB$control$n.burnin                # the length of the burn-in phase
## [1] 3000
jointFitB$control$n.thin                  # thinning
## [1] 10
jointFitB$control$knots                   # knots for the spline basis 
##  [1]  0.002007988  0.002007988  0.002007988  0.002007988  3.771214286  4.963428571  6.155642857
##  [8]  7.347857143  8.540071429  9.732285714 10.924500000 12.116714286 13.308928571 14.501142857
## [15] 15.693357143 16.885571429 18.077785714 21.400000000 21.400000000 21.400000000 21.400000000
jointFitB$control$ordSpline               # order of the spline basis for baseline hazard
## [1] 4
jointFitB$control$seed                    # this is where you set up the seed
## [1] 1
jointFitB$postMeans$betas                 # posterior Mean estimates
##     (Intercept)         obstime obstime:drugddI 
##     7.190337630    -0.231668241     0.008831915
jointFitB$postModes$gammas                # posterior Mode estimates
##   drugddI 
## 0.3490291
jointFitB$StErr$Bs.gammas                 # Standard Errors estimates 
##  Bs.gammas1  Bs.gammas2  Bs.gammas3  Bs.gammas4  Bs.gammas5  Bs.gammas6  Bs.gammas7  Bs.gammas8 
##  0.01829073  0.01476564  0.01306868  0.01217552  0.01160458  0.01218013  0.01204375  0.01228668 
##  Bs.gammas9 Bs.gammas10 Bs.gammas11 Bs.gammas12 Bs.gammas13 Bs.gammas14 Bs.gammas15 Bs.gammas16 
##  0.01251894  0.01312726  0.01445770  0.01588205  0.01666955  0.02161833  0.02635513  0.03316437 
## Bs.gammas17 
##  0.04105986
jointFitB$CIs$alphas                      # ET credible intervals (95 % by default)
##           Assoct
## 2.5%  -0.3833265
## 97.5% -0.2188212
jointFitB$Pvalues                         # Bayesian analogy of p-value through ET CI
## $betas
## [1] 0.000 0.000 0.877
## 
## $sigma
## [1] 0
## 
## $D
## [1] 0.000 0.604 0.604 0.000
## 
## $gammas
## [1] 0.095
## 
## $Bs.gammas
##  [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## 
## $tauBs
## [1] 0
## 
## $alphas
## [1] 0
# jointFitB$vcov                          # Variance-covariance matrix among all model parameters 
head(jointFitB$mcmc$D)                    # sampled chains
##       D[1, 1]     D[2, 1]     D[1, 2]   D[2, 2]
## [1,] 19.87876  0.03836447  0.03836447 0.2996788
## [2,] 22.13644 -0.09128929 -0.09128929 0.3209435
## [3,] 20.74985  0.04069021  0.04069021 0.2889551
## [4,] 22.49089 -0.13321169 -0.13321169 0.3710575
## [5,] 20.36252 -0.10407358 -0.10407358 0.2866503
## [6,] 20.43969 -0.02503158 -0.02503158 0.2987289
lapply(jointFitB$mcmc, hdi)               # Highest Posterior Density Credible Intervals, library(HDInterval)
## $betas
##       (Intercept)    obstime obstime:drugddI
## lower    6.762409 -0.3142609      -0.1111266
## upper    7.613233 -0.1419485       0.1348963
## attr(,"credMass")
## [1] 0.95
## 
## $sigma
##          sigma
## lower 1.619126
## upper 1.819198
## attr(,"credMass")
## [1] 0.95
## 
## $b
##     lower     upper 
## -6.381354  8.131627 
## attr(,"credMass")
## [1] 0.95
## 
## $D
##        D[1, 1]    D[2, 1]    D[1, 2]   D[2, 2]
## lower 18.20064 -0.3793769 -0.3793769 0.2726199
## upper 24.13217  0.2300917  0.2300917 0.3861688
## attr(,"credMass")
## [1] 0.95
## 
## $gammas
##           drugddI
## lower -0.03787297
## upper  0.70092450
## attr(,"credMass")
## [1] 0.95
## 
## $Bs.gammas
##       Bs.gammas1 Bs.gammas2 Bs.gammas3 Bs.gammas4 Bs.gammas5 Bs.gammas6 Bs.gammas7 Bs.gammas8
## lower  -3.338865  -3.135212  -3.021408  -2.900799  -2.845472  -2.832086  -2.776659  -2.753314
## upper  -2.268921  -2.292135  -2.279775  -2.225913  -2.190104  -2.169244  -2.129408  -2.085837
##       Bs.gammas9 Bs.gammas10 Bs.gammas11 Bs.gammas12 Bs.gammas13 Bs.gammas14 Bs.gammas15
## lower  -2.718079   -2.733021   -2.778234   -2.793933   -2.942410   -3.020425   -3.201066
## upper  -2.043946   -2.040454   -2.021664   -1.980983   -2.008022   -1.950891   -1.878983
##       Bs.gammas16 Bs.gammas17
## lower   -3.444652   -3.764131
## upper   -1.762172   -1.616662
## attr(,"credMass")
## [1] 0.95
## 
## $tauBs
##          tauBs
## lower  38.3158
## upper 846.4514
## attr(,"credMass")
## [1] 0.95
## 
## $alphas
##           Assoct
## lower -0.3806329
## upper -0.2180476
## attr(,"credMass")
## [1] 0.95
jointFitB$DIC                             # Deviance Information Criterion
## [1] 474139.7

The outputs of traditional functions resemble the outputs for MLE approach:

summary(jointFitB)
## 
## Call:
## jointModelBayes(lmeObject = lmeFit, survObject = coxFit, timeVar = "obstime")
## 
## Data Descriptives:
## Longitudinal Process     Event Process
## Number of Observations: 1405 Number of Events: 188 (40.3%)
## Number of subjects: 467
## 
## Joint Model Summary:
## Longitudinal Process: Linear mixed-effects model
## Event Process: Relative risk model with penalized-spline-approximated 
##      baseline risk function
## Parameterization: Time-dependent value 
## 
##  LPML      DIC       pD
##  -Inf 474139.7 232406.1
## 
## Variance Components:
##              StdDev    Corr
## (Intercept)  4.5939  (Intr)
## obstime      0.5741 -0.0289
## Residual     1.7188        
## 
## Coefficients:
## Longitudinal Process
##                   Value Std.Err Std.Dev    2.5%   97.5%      P
## (Intercept)      7.1903  0.0054  0.2200  6.7519  7.6088 <0.001
## obstime         -0.2317  0.0012  0.0444 -0.3204 -0.1469 <0.001
## obstime:drugddI  0.0088  0.0018  0.0629 -0.1111  0.1349  0.877
## 
## Event Process
##            Value Std.Err  Std.Dev    2.5%     97.5%      P
## drugddI   0.3296  0.0102   0.1978 -0.0726    0.6783  0.095
## Assoct   -0.2965  0.0021   0.0426 -0.3833   -0.2188 <0.001
## tauBs   381.6132 18.8686 252.9150 67.6810 1011.4651     NA
## 
## MCMC summary:
## iterations: 20000 
## adapt: 3000 
## burn-in: 3000 
## thinning: 10 
## time: 1.1 min
fixef(jointFitB)
##     (Intercept)         obstime obstime:drugddI 
##     7.190337630    -0.231668241     0.008831915
head(coef(jointFitB, "Longitudinal"))
##      (Intercept)    obstime obstime:drugddI
## [1,]    9.871951 -0.1420444     0.008831915
## [2,]    7.091661 -0.2092840     0.008831915
## [3,]    4.598255 -0.1455689     0.008831915
## [4,]    4.445164 -0.2804179     0.008831915
## [5,]    8.219124 -0.1739527     0.008831915
## [6,]    4.150560 -0.4316105     0.008831915
coef(jointFitB, "Event")
##    drugddI     Assoct 
##  0.3295682 -0.2964958
confint(jointFitB)
##                         2.5 %         est.     97.5 %
## Y.(Intercept)      6.75194914  7.190337630  7.6087813
## Y.obstime         -0.32039245 -0.231668241 -0.1469199
## Y.obstime:drugddI -0.11112864  0.008831915  0.1348872
## T.drugddI         -0.07262605  0.329568205  0.6783042
## T.Assoct          -0.38332653 -0.296495759 -0.2188212
# anova(jointFitB)                       # only works for two models
# logLik(jointFitB)                      # why error?

The residual plots by plot are now in plot.JMbayes replaced with traceplots, autocorrelation functions and density estimates (in a window \(2\times 2\)).

plot(jointFitB, which = "trace", param = c("betas", "gammas"))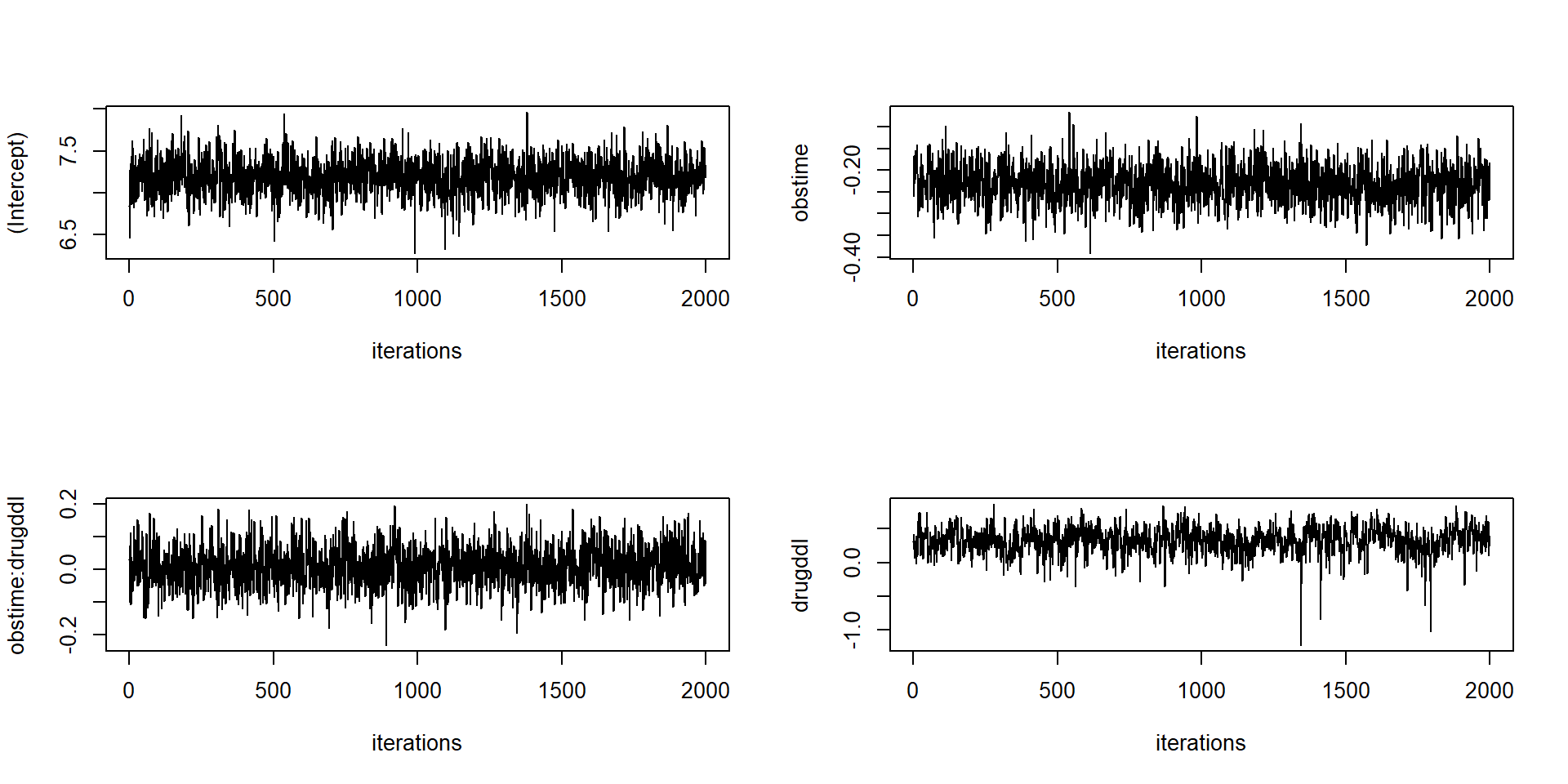

plot(jointFitB, which = "autocorr", param = c("sigma", "D"))

plot(jointFitB, which = "density", param = c("alphas", "betas"))

There is no function for plotting the posterior distribution of the baseline hazard function estimated by splines. We have to explore it on our own:

library(splines)
jointFitB$baseHaz                               # only information about type of splines
## [1] "P-splines"
tgrid <- seq(0, 20, length.out = 101)[-1]
ncoefs <- dim(jointFitB$mcmc$Bs.gammas)[2]
ord <- jointFitB$control$ordSpline
knots <- unique(jointFitB$control$knots)
BSB <- bs(tgrid, degree = ord,
          knots = knots[-c(1,length(knots))], 
          Boundary.knots = knots[c(1,length(knots))])
ncoefs == dim(BSB)[2]                           # great, the number of coefficients matches!
## [1] TRUE
basehaz <- exp(jointFitB$mcmc$Bs.gammas %*% t(BSB))
basehaz_post <- t(apply(basehaz, 2, function(x){
  c(quantile(x, probs = 0.025), mean(x), quantile(x, probs = 0.975))
}))

cumbasehaz <- t(apply(basehaz, 1, function(h){
  # we need cumulative approximation of the integral
  # integral between t1 < t2 with values h(t1) and h(t2) is approximated by
  # (h(t1) + h(t2))/2 * (t2 - t1)
  avg_neighbours <- zoo::rollmean(c(0,h), 2)
  diff_time <- diff(c(0, tgrid))
  ret <- cumsum(avg_neighbours * diff_time)
  return(ret)
}))

cumbasehaz_post <- t(apply(cumbasehaz, 2, function(x){
  c(quantile(x, probs = 0.025), mean(x), quantile(x, probs = 0.975))
}))

par(mfrow = c(1,2), mar = c(4,4,2.5,1))
# Baseline hazard
plot(tgrid, basehaz_post[,2], xlim = c(0, max(breaks)), ylim = c(0.05, 0.15),
     type = "l", col = "saddlebrown", lwd = 2,
     xlab = "Time", ylab = "Hazard", main = "Baseline hazard")
lines(tgrid, basehaz_post[,1], col = "goldenrod", lty = 2)
lines(tgrid, basehaz_post[,3], col = "goldenrod", lty = 2)
legend("top", c("Posterior Mean", "ET CI 95 %"), bty = "n", ncol = 2,
       col = c("saddlebrown", "goldenrod"), lwd = c(2,1), lty = c(1,2))

# Cumulative baseline hazard
plot(c(0,tgrid), c(0, cumbasehaz_post[,2]), xlim = c(0, max(breaks)), ylim = c(0, 2),
     type = "l", col = "saddlebrown", lwd = 2,
     xlab = "Time", ylab = "Hazard", main = "Cumulative baseline hazard")
lines(c(0,tgrid), c(0, cumbasehaz_post[,1]), col = "goldenrod", lty = 2)
lines(c(0,tgrid), c(0, cumbasehaz_post[,3]), col = "goldenrod", lty = 2)
legend("topleft", c("Posterior Mean", "ET CI 95 %"), bty = "n",
       col = c("saddlebrown", "goldenrod"), lwd = c(2,1), lty = c(1,2))

The high baseline hazard for low values of time is probably due to much higher proportion of deaths occurring within the first 2 months:

aids[aids$Time <= 2, ]       # almost all have event = death = 1
##      patient Time death       CD4 obstime drug gender prevOI         AZT start stop event
## 19         6 1.90     1  4.582576       0  ddC female   AIDS     failure     0 1.90     1
## 134       49 2.00     1  1.000000       0  ddI   male noAIDS intolerance     0 2.00     1
## 190       69 0.77     1  2.236068       0  ddC   male   AIDS     failure     0 0.77     1
## 200       73 1.30     1  1.000000       0  ddI   male   AIDS intolerance     0 1.30     1
## 318      108 1.07     1  1.414214       0  ddC   male   AIDS     failure     0 1.07     1
## 571      189 1.83     0 19.235384       0  ddI   male   AIDS intolerance     0 1.83     0
## 594      196 1.70     1  4.472136       0  ddI   male   AIDS intolerance     0 1.70     1
## 889      292 1.43     1  1.732051       0  ddC female   AIDS intolerance     0 1.43     1
## 1030     337 1.13     1  3.464102       0  ddI female   AIDS     failure     0 1.13     1
## 1054     344 1.07     1  2.236068       0  ddC   male   AIDS intolerance     0 1.07     1
## 1086     355 0.47     1 18.466185       0  ddI female noAIDS intolerance     0 0.47     1
## 1141     376 1.63     1  0.000000       0  ddI   male   AIDS     failure     0 1.63     1
## 1251     415 1.03     1  2.000000       0  ddC   male   AIDS intolerance     0 1.03     1
## 1282     427 1.43     1  6.000000       0  ddC   male   AIDS     failure     0 1.43     1
## 1367     453 0.90     1  6.324555       0  ddI female   AIDS     failure     0 0.90     1
## 1401     464 2.00     1  4.898979       0  ddC   male   AIDS intolerance     0 2.00     1

Function predict predicts values for the longitudinal part of a joint model. Its syntax is analogical to the one in MLE approach.

pats <- c(1, 6, 141, 189)
(newdata <- aids[aids$patient %in% pats, ])
##     patient  Time death       CD4 obstime drug gender prevOI         AZT start  stop event
## 1         1 16.97     0 10.677078       0  ddC   male   AIDS intolerance     0  6.00     0
## 2         1 16.97     0  8.426150       6  ddC   male   AIDS intolerance     6 12.00     0
## 3         1 16.97     0  9.433981      12  ddC   male   AIDS intolerance    12 16.97     0
## 19        6  1.90     1  4.582576       0  ddC female   AIDS     failure     0  1.90     1
## 410     141 10.93     1  3.162278       0  ddI   male   AIDS intolerance     0  2.00     0
## 411     141 10.93     1  0.000000       2  ddI   male   AIDS intolerance     2  6.00     0
## 412     141 10.93     1  2.236068       6  ddI   male   AIDS intolerance     6 10.93     1
## 571     189  1.83     0 19.235384       0  ddI   male   AIDS intolerance     0  1.83     0
pred <- predict(jointFitB, newdata = newdata, type = "Subject", interval = "confidence", idVar = "patient")
par(mfrow = c(1,length(pats)), mar = c(4,4,2,0.5))
for(i in 1:length(pats)){
  subnd <- newdata[newdata$patient == pats[i],]
  plot(CD4 ~ obstime, data = subnd,  
       xlab = "Time", ylab = "CD4", main = paste("Patient", pats[i]),
       xlim = range(breaks), ylim = c(0, max(aids$CD4)),
       col = "royalblue", bg = "skyblue", pch = 21, cex = 1.5)
  lines(attr(pred,"time.to.pred")[[i]], pred$pred[1:25 + (i-1)*25], col = "red", lwd = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$low[1:25 + (i-1)*25], col = "orange", lty = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$upp[1:25 + (i-1)*25], col = "orange", lty = 2)
}

Function survfitJM using Monte Carlo predicts the conditional probability of surviving later times than the last observed time for which a longitudinal measurement was available:

surv <- survfitJM(jointFitB, newdata = newdata, idVar = "patient")
par(mfrow = c(1,length(pats)), mar = c(4,4,2,0.5))
plot(surv)

Survival prediction for two patients newly incoming to the study, two different drugs given:

ND <- data.frame(patient = c(1001,1002),
                 obstime = c(0,0),
                 CD4 = c(7,7),                # average CD4 count at obstime == 0
                 drug = factor(c("ddC", "ddI")))
pred <- predict(jointFitB, newdata = ND, type = "Subject", interval = "prediction", idVar = "patient")
surv <- survfitJM(jointFitB, newdata = ND, idVar = "patient")

par(mfrow = c(1,2), mar = c(4,4,2.5,0.5))
COL <- c("goldenrod", "royalblue")
COLlight <- c("gold", "lightblue")

# Prediction of CD4 evolution
plot(0, 0, type = "n",
     xlim = range(breaks), ylim = c(0, max(pred$upp)),
     xlab = "Time", ylab = "CD4", main = "Longitudinal prediction")
points(0, 7, col = "black", bg = "grey", pch = 21, cex = 1.5)
for(i in 1:2){
  lines(attr(pred,"time.to.pred")[[i]], pred$pred[1:25 + (i-1)*25], col = COL[i], lwd = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$low[1:25 + (i-1)*25], col = COLlight[i], lty = 2)
  lines(attr(pred,"time.to.pred")[[i]], pred$upp[1:25 + (i-1)*25], col = COLlight[i], lty = 2)
}
legend("right", levels(ND$drug), bty = "n", title = "Drug", col = COL, lty = 1, lwd = 2)

# Prediction of survival
plot(0, 0, type = "n",
     xlim = range(breaks), ylim = c(0, 1),
     xlab = "Time", ylab = "Survival probability", main = "Survival prediction")
points(0, 1, col = "black", bg = "grey", pch = 21, cex = 1.5)
for(i in 1:2){
  lines(Mean ~ times, data = surv$summaries[[i]], col = COL[i], lwd = 2)
  lines(Lower ~ times, data = surv$summaries[[i]], col = COLlight[i], lty = 2)
  lines(Upper ~ times, data = surv$summaries[[i]], col = COLlight[i], lty = 2)
}
legend("bottomleft", levels(ND$drug), bty = "n", title = "Drug", col = COL, lty = 1, lwd = 2)