



Next: Mapping hierarchy of dendrites
Up: Dendrites
Previous: Gehman dendrite
The concept of the Gehman dendrite has been generalized in [Arévalo et al. 2001, Section 4,
p. 4-10] as follows.
- For each natural number
 there exists topologically unique
dendrite
there exists topologically unique
dendrite 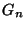 dendrite
dendrite 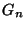 such that
such that
-
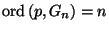 for each point
for each point
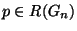 ;
;
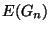 is homeomorphic to the Cantor ternary set.
is homeomorphic to the Cantor ternary set.
(Note that 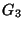 is just the Gehman dendrite
is just the Gehman dendrite 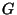 .)
.)
- There exists a
dendrite
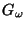 such that
such that
-
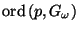 is finite for each point
is finite for each point
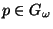 ;
;
-
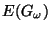 is homeomorphic to the Cantor ternary set;
is homeomorphic to the Cantor ternary set;
- for each natural number
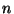 and for each maximal arc
and for each maximal arc 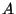 contained in
contained in
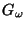 there is a point
there is a point 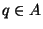 such that
such that
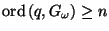 .
.
See Figure A.
Figure 1.3.19:
( A ) 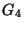
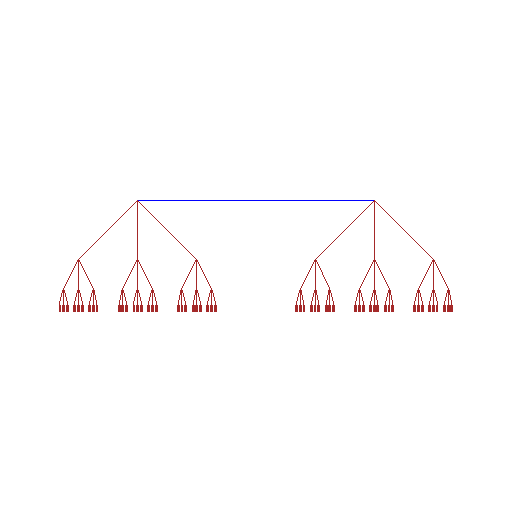 |
The dendrites 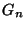 and
and
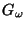 have the following
universality properties.
have the following
universality properties.
- For each natural number
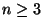 the dendrite
the dendrite 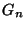 is
universal for the class of all dendrites
is
universal for the class of all dendrites 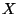 such that
such that
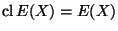 and that
and that
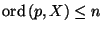 for each
point
for each
point 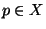 .
.
- Each dendrite
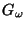 is universal for the class of all
dendrites with the closed set of end points.
is universal for the class of all
dendrites with the closed set of end points.
Here you can find source files
of this example.
Here you can check the table
of properties of individual continua.
Here you can read Notes
or
write to Notes
ies of individual continua.




Next: Mapping hierarchy of dendrites
Up: Dendrites
Previous: Gehman dendrite
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30
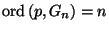 for each point
for each point
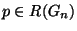 ;
;
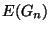 is homeomorphic to the Cantor ternary set.
is homeomorphic to the Cantor ternary set.
![]() is just the Gehman dendrite
is just the Gehman dendrite ![]() .)
.)
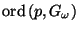 is finite for each point
is finite for each point
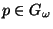 ;
;
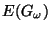 is homeomorphic to the Cantor ternary set;
is homeomorphic to the Cantor ternary set;
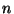 and for each maximal arc
and for each maximal arc 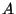 contained in
contained in
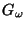 there is a point
there is a point 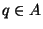 such that
such that
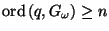 .
.
![]() and
and
![]() have the following
universality properties.
have the following
universality properties.
