Příklad 1
Jsou dány nesoustředné kružnice \(k_1\), \(k_2\). Sestrojte střed stejnolehlosti, ve které se zobrazí kružnice \(k_1\) na kružnici \(k_2\). Určete koeficient stejnolehlosti.
Rozbor
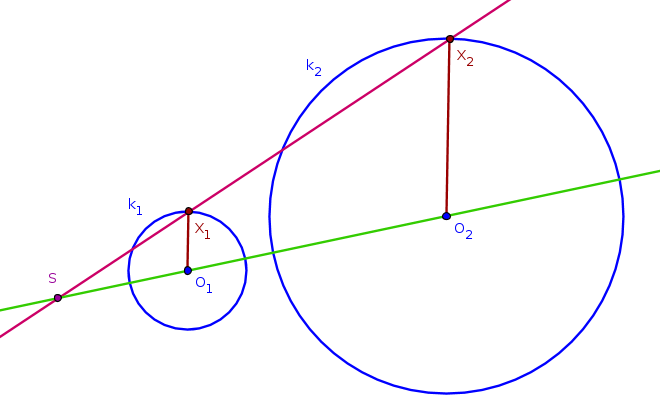
Obr. 4.1.6 - Náčrtek příkladu 1
- Z definice stejnolehlosti plyne, že libovolná úsečka \(XY\) se zobrazí na úsečku \(X'Y'\), přičemž \(XY\parallel X'Y'\) a \(|X'Y'|=|\kappa|\cdot|XY|\), kde \(\kappa\) je koeficient stejnolehlosti. Toho využijeme k získání středu stejnolehlosti.
- Střed \(O_1\) kružnice \(k_1\) se v hledané stejnolehlosti se středem \(S\) a koeficientem \(\kappa\) zobrazí na střed \(O_2\) kružnice \(k_2\). Zvolme libovolný bod \(X_1\) na kružnici \(k_1\). Pak se úsečka \(X_1O_1\) zobrazí na úsečku \(X_2O_2\) s ní rovnoběžnou.
- Protože se bod \(X_1\) má v dané stejnolehlosti zobrazit na bod \(X_2\), bude bod \(X_2\) ležet na polopřímce \(SX_1\) (nebo na polopřímce k ní opačné). Sestrojíme přímku \(X_1X_2\), průsečík přímky \(X_1X_2\) a přímky \(O_1O_2\) bude hledaný střed stejnolehlosti, ve které se kružnice \(k_1\) zobrazí na kružnici \(k_2\).
- Jelikož platí \(|O_2X_2|=|\kappa|\cdot|O_1X_1|\), bude \(|\kappa|=\frac{|O_2X_2|}{|O_1X_1|}\). Koeficient \(\kappa\) bude kladný, pokud bude bod \(X_2\) ležet na polopřímce \(SX_1\). Pokud bude ležet na polopřímce opačné k \(SX_1\), bude koeficient záporný.
Konstrukce a zápis konstrukce
Applet 4.1.9 - Příklad 1
Diskuse
- Úloha má 2 řešení, pokud mají kružnice \(k_1\) a \(k_2\) různé poloměry.
- Úloha má 1 řešení, pokud mají kružnice stejné poloměry.
Poznámka
Pokud by byly kružnice \(k_1\) a \(k_2\) soustředné, pak by střed stejnolehlosti splýval se středem kružnic.
Další příklady
| Příklad 1 | Příklad 2 |
