- RINALDO M. COLOMBO

Department of Mathematics, Brescia University, Via Branze 38, 25123 Brescia, Italy
email: Rinaldo@Ing.UniBs.It
home: http://bsing.ing.unibs.it/~rinaldo/Wave Front Tracking in Systems of Conservation Laws
Abstract:
Wave Front Tracking is a set of techniques to construct approximate solutions to hyperbolic conservation laws, i.e. to first order quasilinear systems of partial differential equations of the form
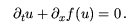
These lectures will introduce the use of Wave Front Tracking and present some recent analytical results obtained through it. Depending on the preferences of the audience, applications to ideal gas dynamics, liquid - vapor phase transitions, combustion models or traffic flow will be considered.
References
- A. Bressan: Hyperbolic Systems of Conservation Laws, Oxford Lecture Series in Mathematics and its Applications.
- A. Bressan: The semigroup approach to systems of conservation laws. Fourth Workshop on Partial Differential Equations, Part I (Rio de Janeiro, 1995). Mat. Contemp. 10 (1996), 21-74.
- H. Holden, N.H. Risebro: Front Tracking for Hyperbolic Conservation Laws, Springer Verlag.
- C. Dafermos: Polygonal approximations of solutions of the initial value problem for a conservation law. J. Math. Anal. Appl. 38 (1972), 33-41.
- C. Dafermos: Hyperbolic Conservation Laws in Continuum Physics. Springer Verlag.
- BENOIT PERTHAME

Ecole Normale Superieure, DMA, 45, rue d'Ulm, F 75230 Paris Cedex 05, France
email: Benoit.Perthame@ens.fr
home: http://www.dma.ens.fr/users/perthame/An Introduction to Mathematical Analysis of Transport equations Arising in Biology
Abstract:
Numerous transport phenomena arise in various areas of biology and related sciences. This course will give an introduction to several examples of such equations and of the corresponding mathematical theories. It will especially cover the following questions
- Structured populations dynamics (L1 methods, eigevalues, time convergence). These arise for instance in age structured models, hidden biological parameters, cell division, phytoplanctons modelling)
- Chemotaxis, angiogenesis. Macoroscopic behaviour and micro-macro scales (these arise in the description of some bacterias motions, cancer therapy)
- Front propagations in ecology. The basic models aim to describe the spread of plants or of organisms (Fisher equation, jump processes)
- A simple example for immune system: evolution and virulence
- MICHAEL RUZICKA

Institute for Applied Mathematics, Eckerstr. 1, Freiburg University, 79104 Freiburg / Brsg., Germany
email: rose@mathematik.uni-freiburg.de
home: http://www.mathematik.uni-freiburg.de/IAM/homepages/rose/Analysis of Electrorheological Fluids
Abstract:
Electrorheological fluids are special viscous fluids which can change dramatically their mechanical properties in dependence on an applied electrical field. This property can be exploited in many technological applications, e.g. clutches, actuators or rehabilition equipement to name a few. The motion of electrorheological fluids can be modelled based on general balance laws of thermodynamics and electrodynamics using the physical properties of the fluid, experimental observations and a non-dimensionalization in order to simplify the system. The resulting system
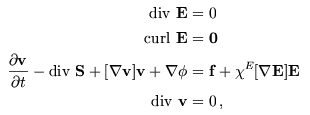
describes the complex interaction between the mechanical and electrical fields. Many experimental observations can be captured by the following constitutive equation for the extra stress tensor

In general, the power p is a function of the modulus of the electric field |E| and thus the above system possesses so called non-standard growth conditions. The canonical energy space of the above system consists of generalized Sobolev and Lebesgue spaces W k,p(.), 1 < p(.) < infty, k \in N0. In the lectures we will discuss the following points: basic properties of generalized Sobolev and Lebesgue spaces, classical linear equations in generalized Sobolev and Lebesgue spaces, mathematical modeling of electrorheological fluids, existence and uniqueness results for weak and strong solutions for large data, error estimates for a corresponding time discretization.
- MISHA VISHIK

Department of Mathematics, The University of Texas at Austin, Austin, TX 78712, U.S.A.
email: vishik@math.utexas.edu
home: http://www.ma.utexas.edu/users/vishik/Instability in Ideal Fluids
Abstract:
- Spectrum of small oscillations of an ideal fluid about a smooth equilibrium. Ray method of constructing approximate evolution operator. Boundedness theorems for pseudodifferential operators.
- Calkin's algebra and Nussbaum's formula. Description of the essential spectrum; essential spectral radius. Examples of flows with a nontrivial discrete spectrum.
- Fluid instabilities and Lyapunov-Oseledets exponents. "Dynamical systems" proofs of instability.
- The growth bound and the spectral bound in L2.
- Linear instability and nonlinear (Lyapunov) instability: analogues of Lyapunov's theorem for 2D incompressible flows.
Every lecturer gave a series of four lectures of the length of 70 minutes each, including discussion. See the general layout of the conference for more details.
The participants of the conference presented their results in the form of short communications (15 minutes) and/or they can exhibited their papers, preprints and books (the number of these was not limited, and they were be related to other scientific areas; the idea is that there was an exhibition place located within the hotel, on which the papers and preprints were exhibited during the whole school).