Theory

The Kaplan-Meier [KM] estimator of the survival function is \[ \widehat{S}(t)=\prod_{\{i: t_i\leq t\}}\biggl[1-\frac{\Delta\overline{N}(t_i)}{\overline{Y}(t_i)}\biggr]. \] A uniformly consistent estimator of the variance of \(\sqrt{n}[\widehat{S}(t)-S(t)]\) is \[ \widehat{V}(t)=\widehat{S}^2(t)\widehat{\sigma}(t)= \widehat{S}^2(t)\int_0^t \frac{n \,\mathrm{d}\overline{N}(u)}{\overline{Y}(u)[\overline{Y}(u)-\Delta\overline{N}(u)]} = \widehat{S}^2(t) \cdot n \cdot \sum \limits_{\{j:t_j \leq t\}} \dfrac{\Delta \overline{N}(t_j)}{\overline{Y}(t_j)[\overline{Y}(t_j)-\Delta\overline{N}(t_j)]} \] (Greenwood formula).

An asymptotic pointwise \(100(1-\alpha)\)% confidence interval for \(S(t)\) at a fixed \(t\) is \[ \biggl( \widehat{S}(t)\Bigl[1-u_{1-\alpha/2}\sqrt{\widehat{\sigma}(t)/n}\Bigr],\, \widehat{S}(t)\Bigl[1+u_{1-\alpha/2}\sqrt{\widehat{\sigma}(t)/n}\Bigr] \biggr). \] Asymptotic simultaneous \(100(1-\alpha)\)% Hall-Wellner confidence bands for \(S(t)\) over \(t\in\langle 0,\tau\rangle\) (for some pre-specified \(\tau\)) are \[ \biggl( \widehat{S}(t)\Bigl\{1-k_{1-\alpha}(\widehat{K}(\tau))\bigl[1+\widehat{\sigma}(t)\bigr]/\sqrt{n}\Bigr\},\, \widehat{S}(t)\Bigl\{1+k_{1-\alpha}(\widehat{K}(\tau))\bigl[1+\widehat{\sigma}(t)\bigr]/\sqrt{n}\Bigr\} \biggr), \] where \(\widehat{K}(t)=\widehat{\sigma}(t)/[1+\widehat{\sigma}(t)]\) and \(k_{1-\alpha}(t)\), \(t\in(0,1\rangle\), satisfies the equation \[ \text{P}\bigl[\sup_{u\in\langle 0,t\rangle}|B(u)|>k_{1-\alpha}(t)\bigr]=\alpha, \] where \(B\) is the Brownian bridge.

There are variations of confidence intervals and confidence bounds for \(S(t)\) based on various transformations (\(\log\), \(\log(-\log)\), \(\arcsin\), …). Formulae for these intervals can be derived by the delta method.

The use of the delta-method: pointwise CI.

Implementation in R

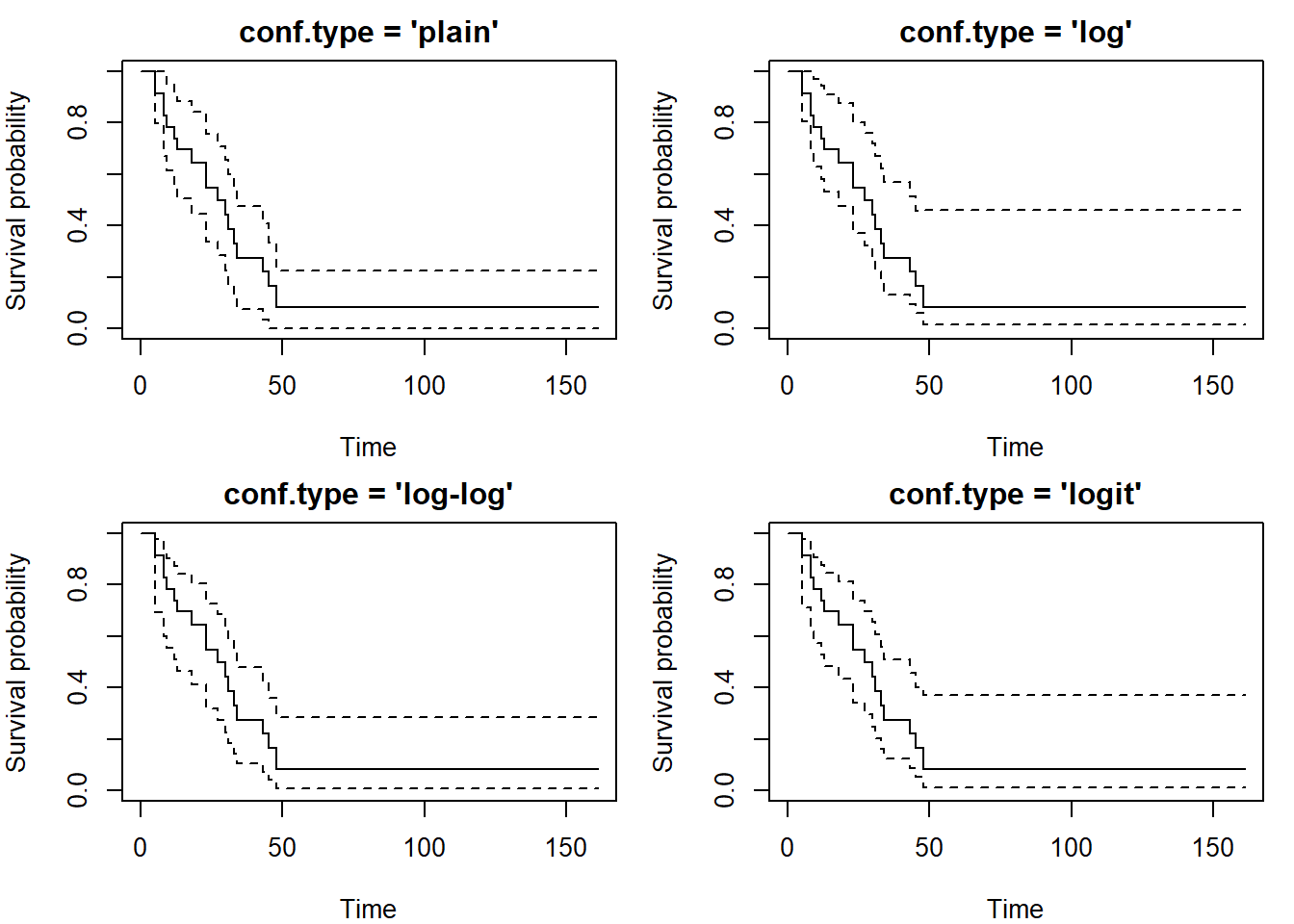
Pointwise confidence intervals

The function survfit in the library survival calculates pointwise confidence intervals. The argument conf.type specifies the transformation (conf.type="plain" means no transformation), the argument conf.int specifies the coverage probability (default 0.95). Be careful, the default value is conf.type="log"!

Regardless of selected conf.type, variable std.err always refers to \(\sqrt{ \widehat{\sigma}(t)/n}\), which can be computed as follows:

se <- sqrt(cumsum(fit$n.event/(fit$n.risk*(fit$n.risk-fit$n.event))))
summary(fit$std.err - se)

Confidence intervals are stored in the output object of the function survfit, the components are called upper and lower. The contents of survfit objects can be also displayed by the function summary.

The function plot called on survfit objects plots the confidence intervals included in the input object. The argument conf.int determines whether or not confidence intervals are plotted (NA for no plotting, otherwise coverage with default 0.95).

For demonstration we will again use aml dataset from library(survival).

library("survival")
fit <- survfit(Surv(time,status)~1, data=aml, conf.type="plain", conf.int=0.9)
summary(fit)
## Call: survfit(formula = Surv(time, status) ~ 1, data = aml, conf.type = "plain", 
##     conf.int = 0.9)
## 
##  time n.risk n.event survival std.err lower 90% CI upper 90% CI
##     5     23       2   0.9130  0.0588       0.8164        1.000
##     8     21       2   0.8261  0.0790       0.6961        0.956
##     9     19       1   0.7826  0.0860       0.6411        0.924
##    12     18       1   0.7391  0.0916       0.5885        0.890
##    13     17       1   0.6957  0.0959       0.5378        0.853
##    18     14       1   0.6460  0.1011       0.4796        0.812
##    23     13       2   0.5466  0.1073       0.3702        0.723
##    27     11       1   0.4969  0.1084       0.3186        0.675
##    30      9       1   0.4417  0.1095       0.2615        0.622
##    31      8       1   0.3865  0.1089       0.2074        0.566
##    33      7       1   0.3313  0.1064       0.1563        0.506
##    34      6       1   0.2761  0.1020       0.1083        0.444
##    43      5       1   0.2208  0.0954       0.0640        0.378
##    45      4       1   0.1656  0.0860       0.0241        0.307
##    48      2       1   0.0828  0.0727       0.0000        0.202
par(mar = c(4,4,1,1))
plot(fit, conf.int=TRUE, xlab = "Time", ylab = "Survival probability")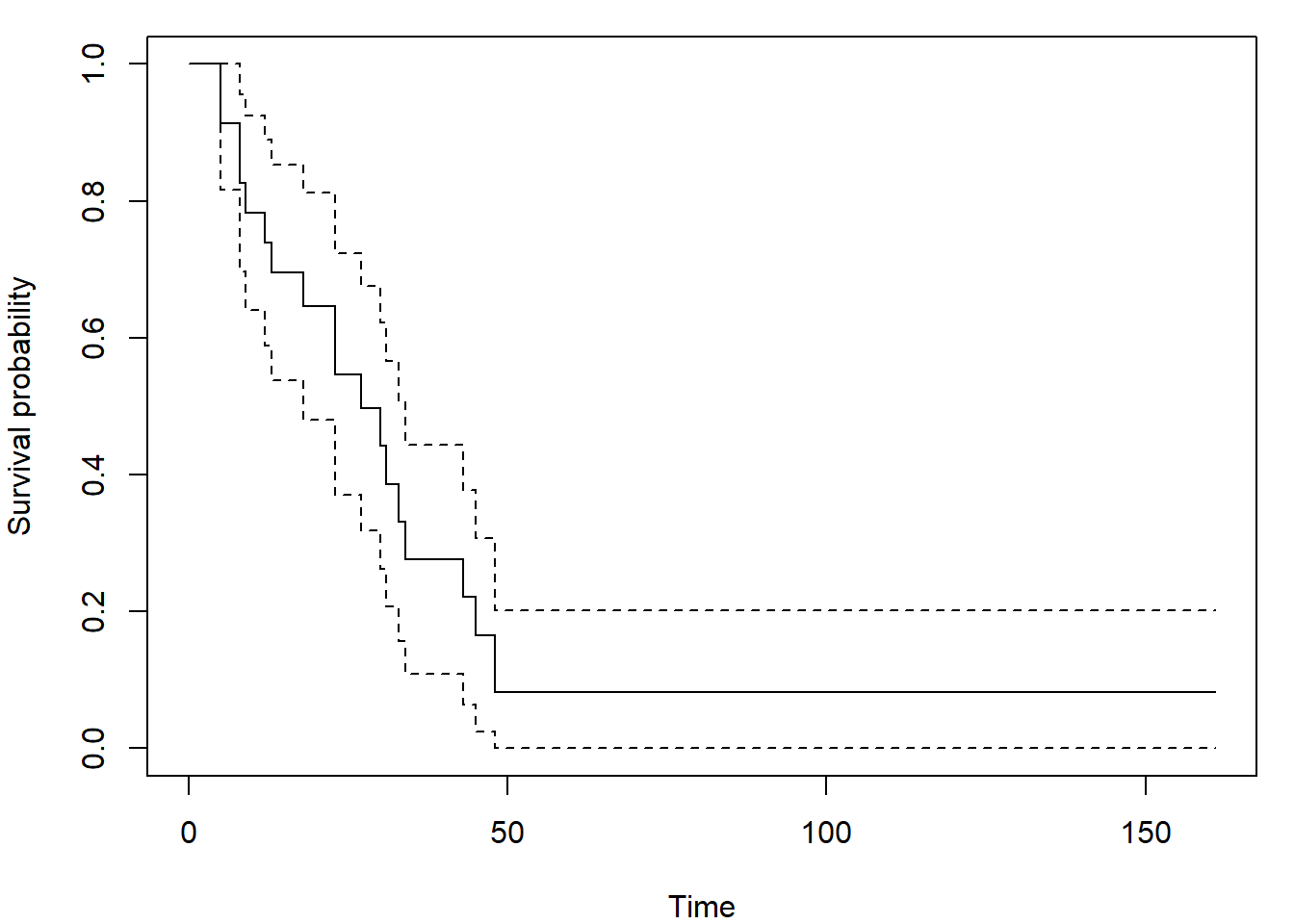


You may also compute and plot confidence intervals for several groups:

fit_grouped <- survfit(Surv(time,status)~x, data=aml, conf.type="plain", conf.int=0.9)
par(mar = c(4,4,1,1))
plot(fit_grouped[1], conf.int=TRUE, col="green", xlab = "Time", ylab = "Survival probability")
lines(fit_grouped[2], conf.int=TRUE, col="magenta")
legend("topright", levels(aml$x), col = c("green","magenta"), lty = 1, bty = "n")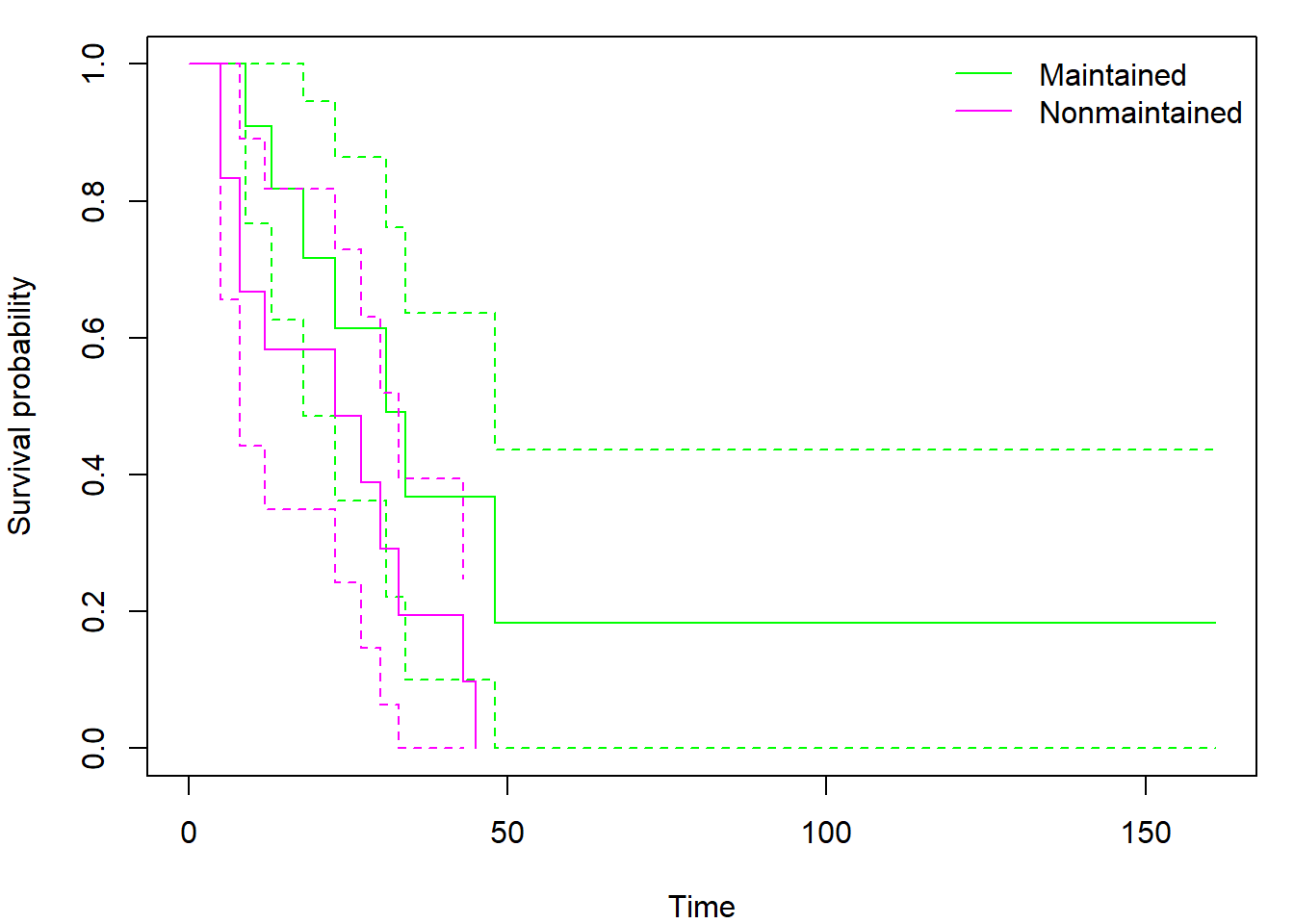

You can also use library(ggplot2) in cooperation with library(survminer) to obtain nicer plots:

library(survminer)
library(ggplot2)
ggsurvplot(fit_grouped, conf.int = 0.95, censor= F,
           ggtheme = theme_minimal())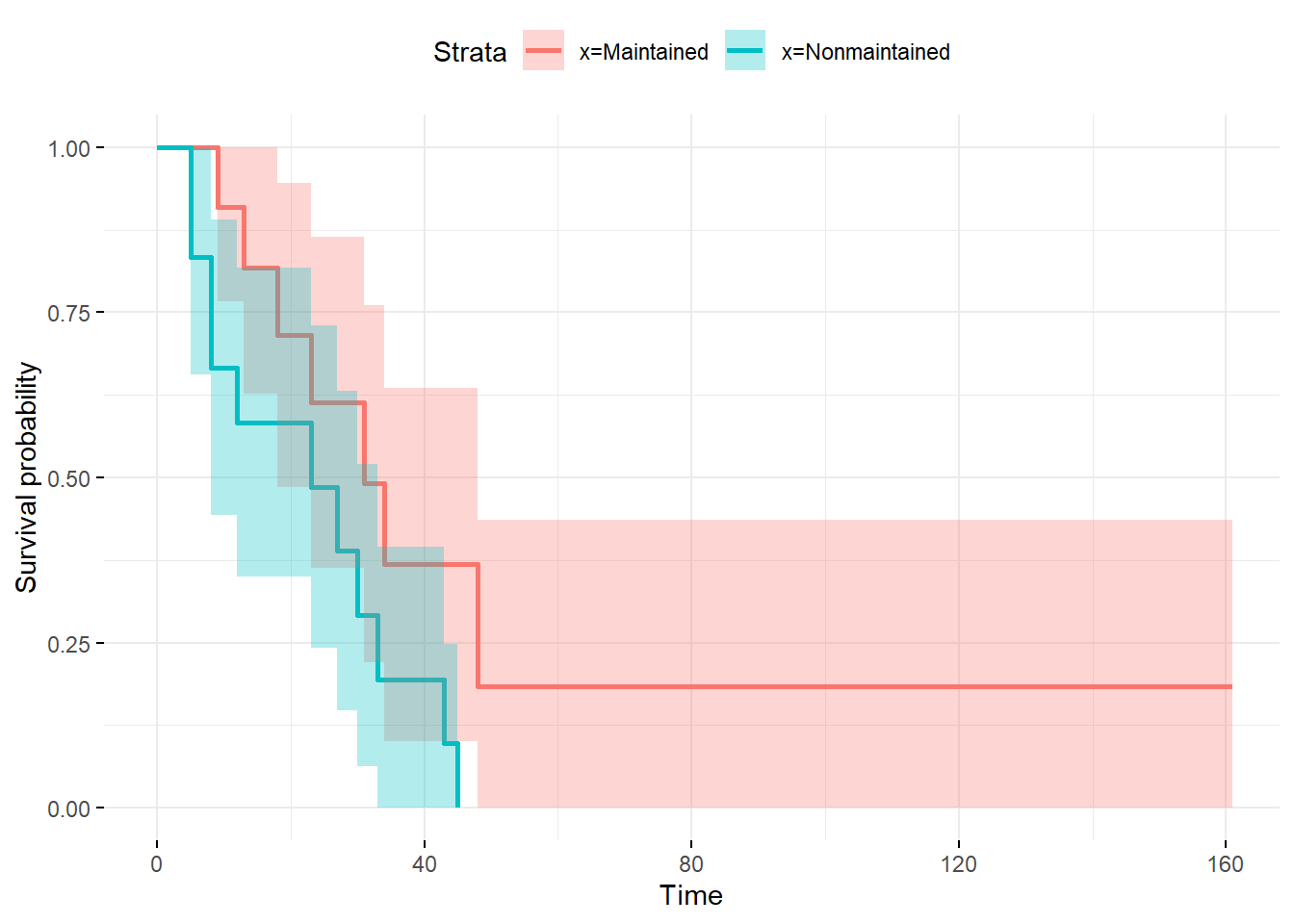

The function ggsurvplot inherits the chosen confidence interval from the survfit object.

Simultaneous confidence bands

There are two different R libraries that can calculate Hall-Wellner simultaneous confidence bands.

1) library(km.ci)

This library includes a function called km.ci, which requires a survfit object as the input and returns another survfit object with recalculated lower and upper components. The output can be processed by any function that accepts survfit objects – e.g., plot, summary, lines.

library("km.ci")
fit <- survfit(Surv(time,status)~1, data=aml, conf.type="plain", conf.int=0.95)
out <- km.ci(fit, conf.level=0.95, tl=5, tu=48, method="hall-wellner") 
par(mar = c(4,4,1,1))
plot(out, xlab = "Time", ylab = "Survival Probability")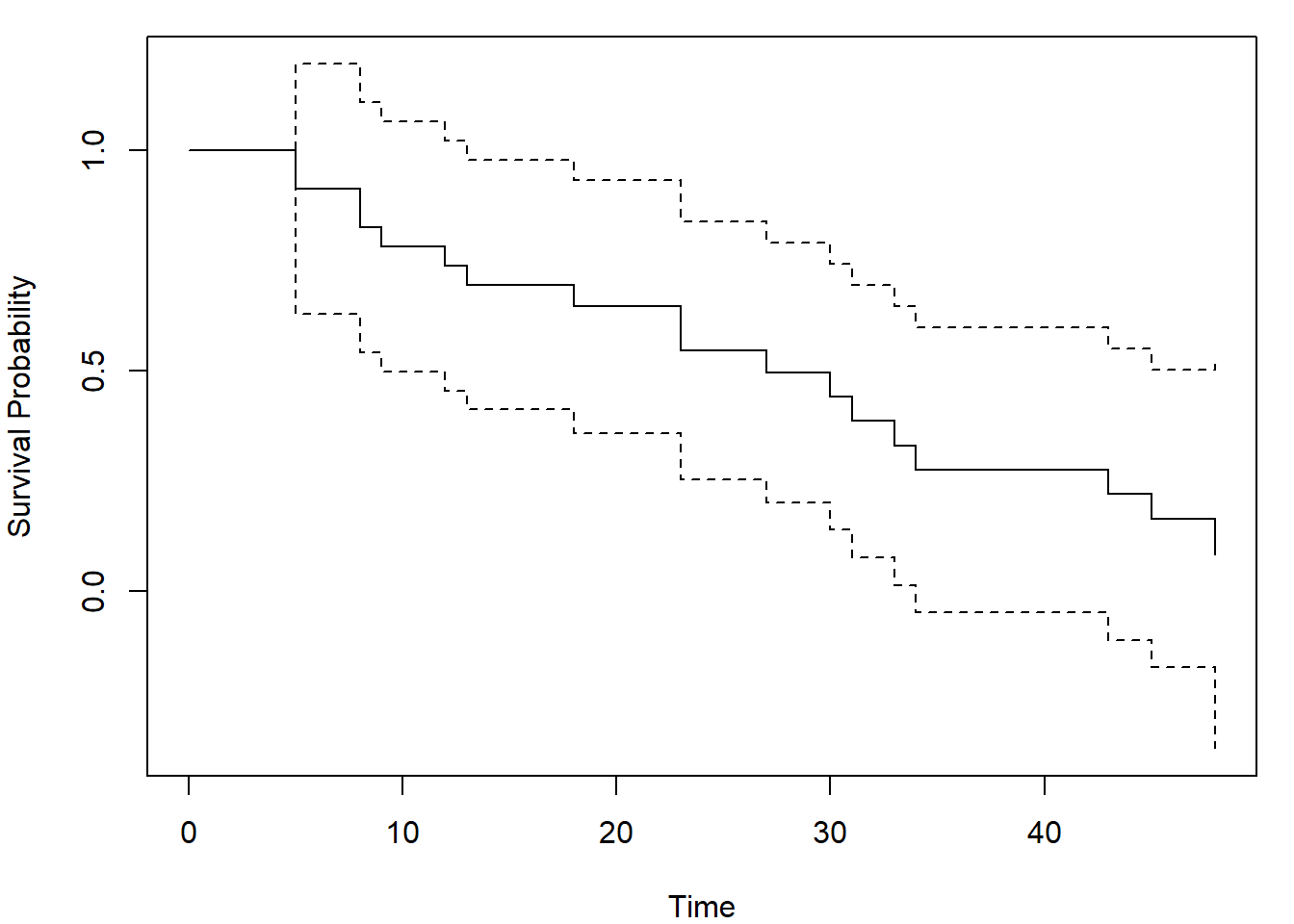

The arguments tl and tu are lower and upper limits of the interval for which the bands are calculated. Not all choises of these limits will lead to a useful result, so be careful and try different inputs. Default values are set to the smallest and largest event time (tl = min(aml$time[as.logical(aml$status)]) = 5, tu = max(aml$time[as.logical(aml$status)]) = 48).

Other methods for calculating confidence intervals are the following:

  • pointwise: peto, linear, log, loglog, rothman, grunkemeier,
  • simultaneous: hall-werner, loghall, epband, logep.

See Details of km.ci function for explanation of these abbreviations.

2) library(OIsurv)

This library includes a function called confBands, which requires a survival object (just Surv) as the input and returns a list of three vectors (time, lower, upper). There is a method for plotting lines from a confBands object, but no method for plot!

Caution

The library OIsurv has been removed from CRAN. The last version can still be installed from an archive, e.g. by the command

install.packages("http://www.karlin.mff.cuni.cz/~vavraj/cda/data/OIsurv_0.2.zip", repos =NULL)
## or from github if you use R-version 4.0.0 or higher
library("remotes")
install_github("cran/OIsurv")

Then one can obtain Hall-Wellner confidence bands as follows

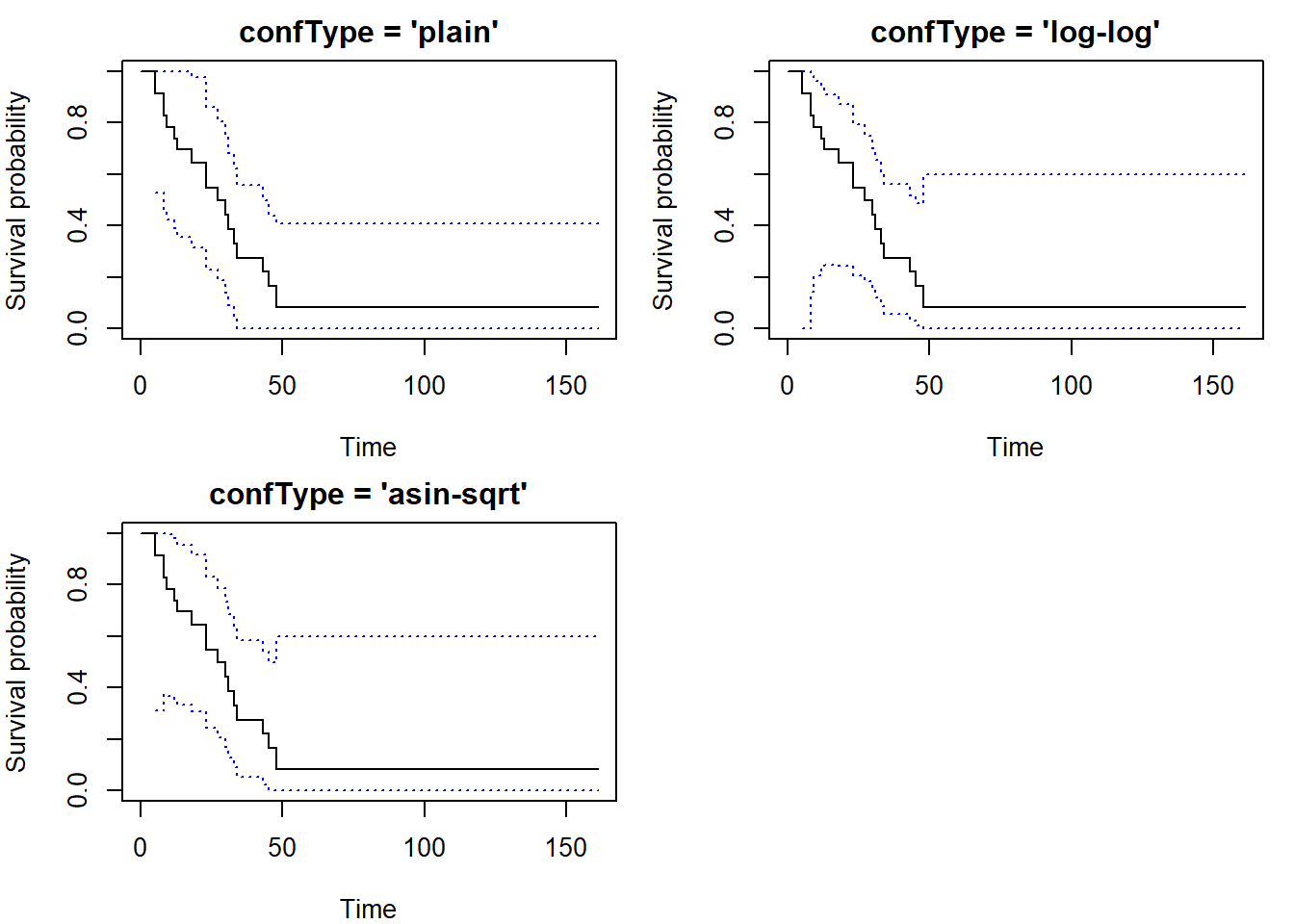
library("OIsurv")
out <- confBands(Surv(aml$time,aml$status), confType="plain", confLevel=0.95, type="hall", tU=160)
par(mar = c(4,4,1,1))
plot(fit, xlab = "Time", ylab = "Survival probability", ylim = c(0,1))
lines(out, lty = 3, col = "blue")
legend("topright", c("Kaplan-Meier", "Pointwise confidence interval", "Hall-Werner confidence bands"),
       col = c("black", "black", "blue"), lty = c(1,2,3), bty = "n")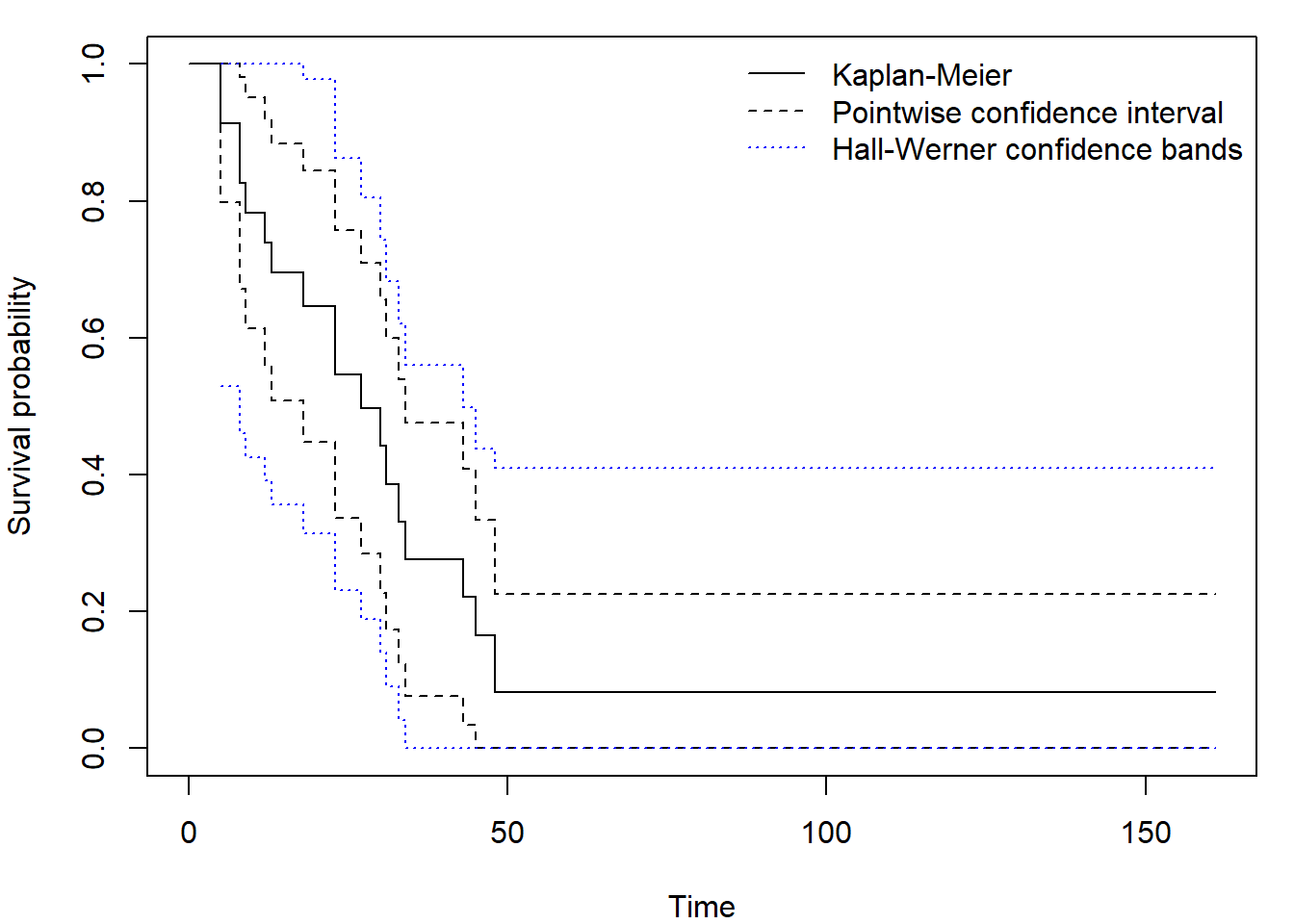

Again be careful when setting minimum tL and maximum tU time value, the defaults are

  • tL = min(aml$time) = 5 = first observed or censored time,
  • tU = max(aml$time) = 161 = last observed time.

Only confidence levels confLevel = c(0.9, 0.95, 0.99) are accepted - default is 0.9!

Argument type differentiates between Equal precision bands ("ep") and Hall-Werner ("hall" or just "h"). You can also use different versions obtained by application of Delta theorem: confType = c("plain", "log-log", "asin-sqrt").


Task 1

Download the dataset km_all.RData.

The dataframe inside is called all. It includes 101 observations and three variables. The observations are acute lymphatic leukemia [ALL] patients who had undergone bone marrow transplant. The variable time contains time (in months) since transplantation to either death/relapse or end of follow up, whichever occured first. The outcome of interest is time to death or relapse of ALL (relapse-free survival). The variable delta includes the event indicator (1 = death or relapse, 0 = censoring). The variable type distinguishes two different types of transplant (1 = allogeneic, 2 = autologous).

Calculate and plot the Kaplan-Meier estimate, 95% pointwise confidence intervals and 95% Hall-Wellner confidence bounds for all patients together, for patients with allogeneic transplants, and for patients with autologous transplants.


Task 2

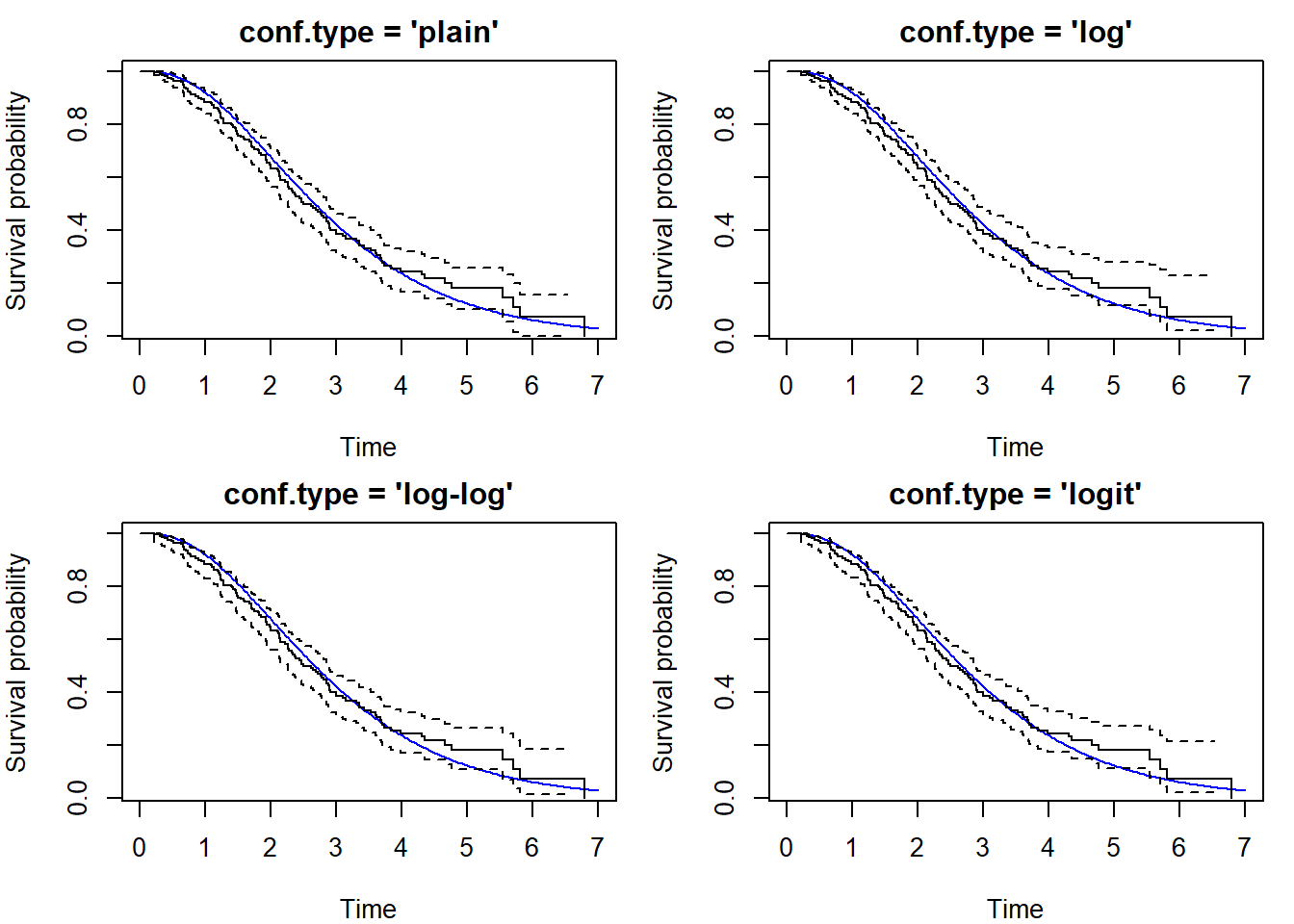
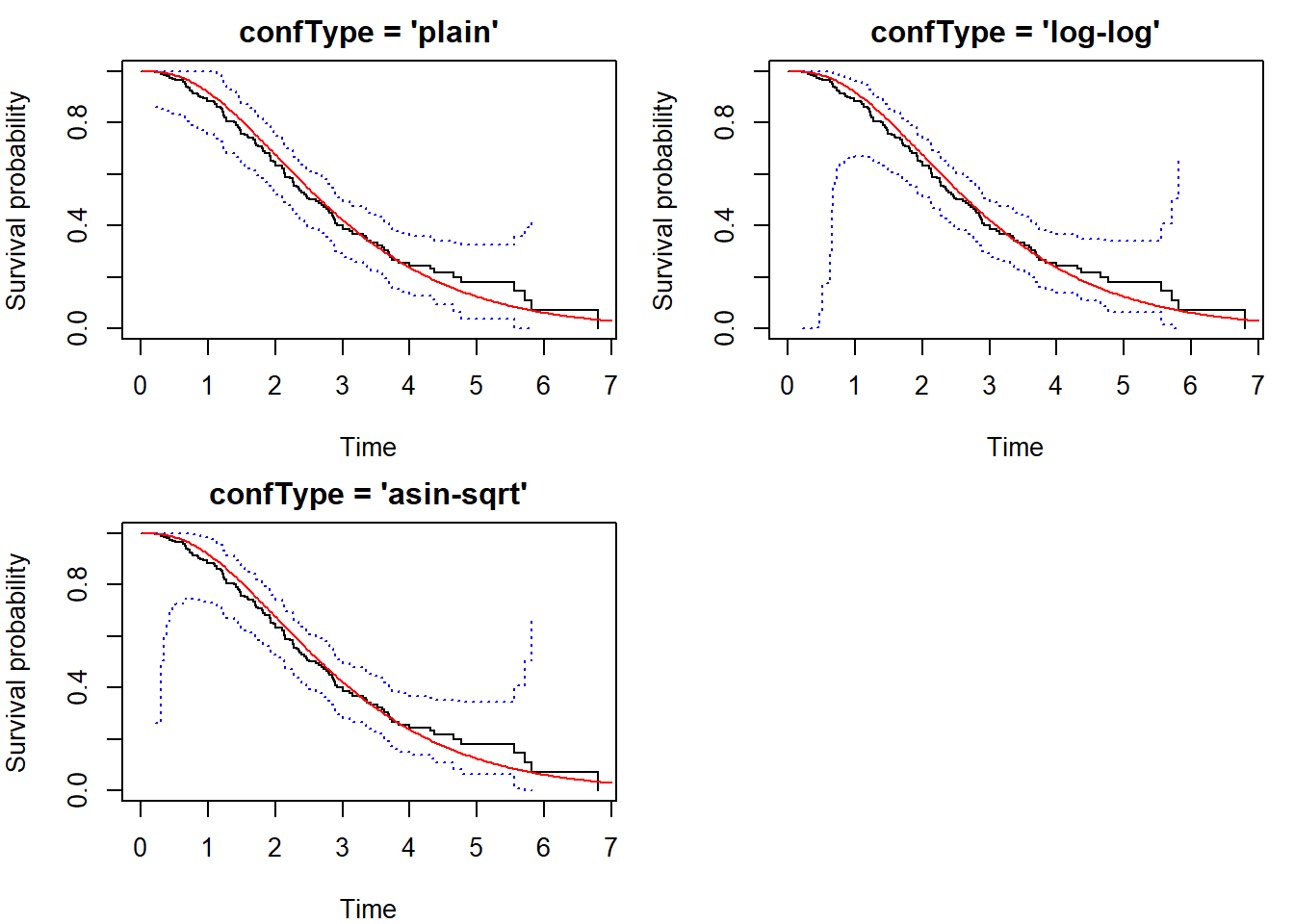
Generate \(n=50\) censored observations as follows: the survival distribution is Weibull with shape parameter \(\alpha=0.7\) and scale parameter \(1/\lambda=2\). Its expectation is \(\Gamma(1+1/\alpha)/\lambda=2\Gamma(17/7)\doteq 2.53\). The censoring distribution is exponential with rate \(\lambda=0.2\) (the expectation is \(1/\lambda=5\)), independent of survival.

Calculate and plot the Kaplan-Meier estimator of \(S(t)\) together with 95% pointwise confidence intervals and 95% Hall-Wellner confidence bounds. Include the true survival function in the plot (use a different color). Include a legend explaining which curve is which and comment on the coverage.

  • Deadline for report: Monday 5th December at 9:00


Task 3 (voluntary)

Conduct a simulation study with data created according to Task 2 assignment. Generate such datasets repeatedly and estimate the probability that the true survival curve is wholly covered by the 95% pointwise confidence intervals and 95% Hall-Wellner confidence bounds (restrict the task to a reasonable finite interval).