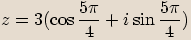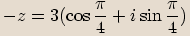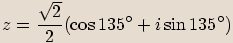Rovnost komplexních čísel v goniometrickém tvaru
Definice
Dvě komplexní čísla v goniometrickém tvaru se rovnají, pokud se rovnají jejich absolutní hodnoty a jejich
argumenty se liší o 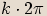 , kde
, kde 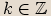 .
.
Číslo komplexně sdružené
Definice
Komplexně sdružená čísla
Komplexně sdruženým číslem ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 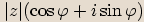 nazveme číslo
nazveme číslo 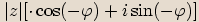 .
Toto komplexně sdružené číslo označujeme
.
Toto komplexně sdružené číslo označujeme  .
.

 a
a nazveme navzájem komplexně sdružená,
nazveme navzájem komplexně sdružená,pokud se rovnají jejich
absolutní hodnoty a jejich argumenty se liší
pouze znaménkem, tj.  a
a  .
.
Poznámka
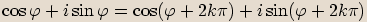 , a tedy čísla
, a tedy čísla 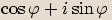 a
a 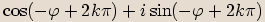 jsou komplexně sdružená.
jsou komplexně sdružená.
Poznámka
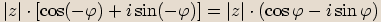 , a proto čísla
, a proto čísla 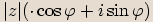 a
a 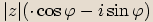 jsou komplexně sdružená.
jsou komplexně sdružená.
Poznámka
Argumenty komplexně sdružených čísel jsou opačné. Protože sinus je lichá funkce
a zároveň kosinus funkce sudá,
projeví se toto při zápisu čísel v algebraickém tvaru pouze u
imaginárních částí. To znamená, že
znaménka u 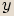 -
ových souřadnic budou opačná, zatímco znaménka u
-
ových souřadnic budou opačná, zatímco znaménka u 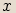 -
ových souřadnic zůstanou
nezměněna.
-
ových souřadnic zůstanou
nezměněna.
Příklady
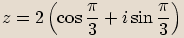

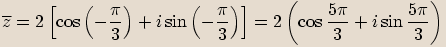



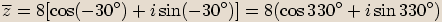

Opačné číslo
Definice
Opačná čísla
Opačným číslem ke komplexnímu číslu  vyjádřenému ve tvaru
vyjádřenému ve tvaru 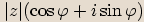 nazveme číslo
nazveme číslo 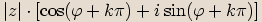 , kde
, kde 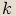 je liché celé číslo.
Toto opačné číslo označujeme
je liché celé číslo.
Toto opačné číslo označujeme 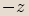 .
.

absolutní hodnoty a jejich argumenty se liší o lichý násobek
 .
.
Poznámka
Argumenty se liší o 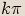 , kde
, kde 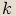 je liché celé číslo, protože obrazy musí být středově
souměrné podle počátku soustavy souřadnic, tj. musí se změnit
je liché celé číslo, protože obrazy musí být středově
souměrné podle počátku soustavy souřadnic, tj. musí se změnit 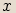 -ová i
-ová i 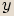 -ová souřadnice.
-ová souřadnice.
Příklady