Cantor organ and accordion

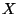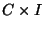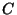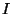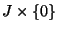The Cantor organ is the union of the product of the Cantor ternary set and the unit interval and all segments of the form or 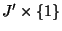, where 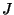(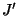, resp.) is the closure of a component of 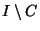of length 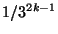( 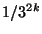), 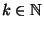[Kuratowski 1968, p. 191]. See Figure A.

Figure 4.1.2: ( A ) Cantor organ

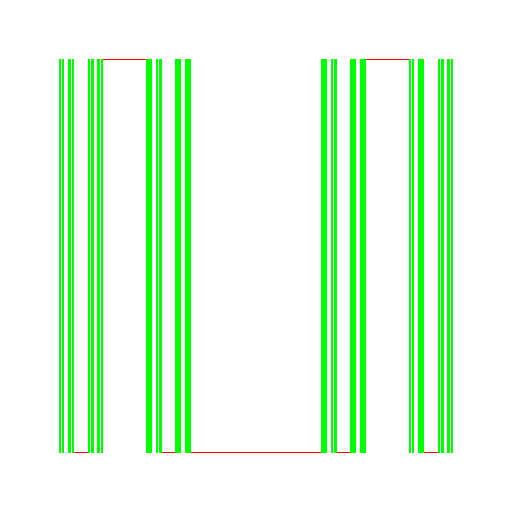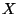1. is an arc-like continuum which is irreducible between points 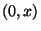and 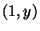, where 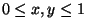, and has exactly four end points.
2. It has uncountably many arc components.

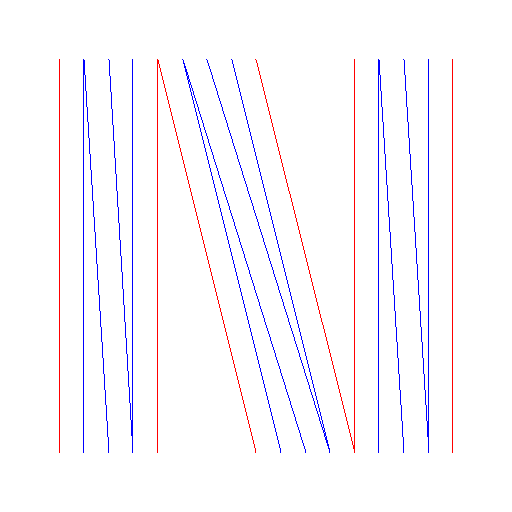
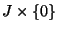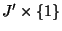A variation of the Cantor organ is the Cantor accordion which is defined as the monotone image of under a map that shrinks horizontal bars and to points [Kuratowski 1968, p. 191]. See Figure B.

Figure 4.1.2: ( B ) Cantor accordion

Besides the above properties,

• has an upper semi-continuous monotone decomposition into arcs with the quotient space an arc.

Here you can find source files of this example.

Here you can check the table of properties of individual continua.

Here you can read Notes or write to Notes ies of individual continua.