



Next: locally
Up: Definitions
Previous: light
If 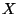 is a metric space, a mapping
is a metric space, a mapping 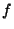 from
from 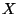 to a space
to a space
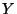 is an
is an
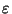 -map if, for each point
-map if, for each point 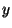 of
of 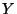 ,
,
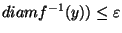 . If
. If 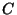 is a
collection of continua, a continuum
is a
collection of continua, a continuum 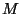 is
is
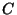 -like if, for every positive number
-like if, for every positive number
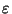 , there
exists an
, there
exists an
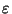 -map of
-map of 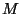 onto an element of
onto an element of 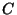 .
In particular, a continuum is tree-like if, for some
collection
.
In particular, a continuum is tree-like if, for some
collection 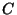 of trees,
of trees, 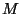 is
is 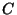 -like.
A concept of a tree-like continuum can be defined in several
(equivalent) ways. One of them is the following. A continuum
-like.
A concept of a tree-like continuum can be defined in several
(equivalent) ways. One of them is the following. A continuum 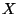 is said to be tree-like
provided that for each
is said to be tree-like
provided that for each
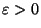 there is a tree
there is a tree 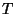 and a surjective
mapping
and a surjective
mapping
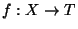 such that
such that 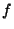 is an
is an
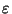 -mapping (i.e.,
-mapping (i.e.,
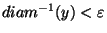 for each
for each 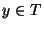 ). Let us mention that a continuum
). Let us mention that a continuum 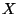 is
tree-like if and only if it is the inverse limit of an inverse
sequence of trees with surjective bonding mappings. Compare e.g.
[Nadler 1992, p. 24].
Using a concept of a nerve of a covering, one can reformulate the above
definition saying that a continuum
is
tree-like if and only if it is the inverse limit of an inverse
sequence of trees with surjective bonding mappings. Compare e.g.
[Nadler 1992, p. 24].
Using a concept of a nerve of a covering, one can reformulate the above
definition saying that a continuum 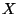 is be tree-like provided that for each
is be tree-like provided that for each
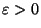 there is an
there is an
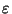 -covering of
-covering of 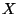 whose nerve is a tree.
whose nerve is a tree.
Finally, the original definition using tree-chains can be found e.g. in
Bing's paper [Bing 1951, p. 653].




Next: locally
Up: Definitions
Previous: light
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-11-30