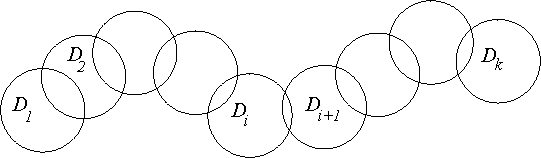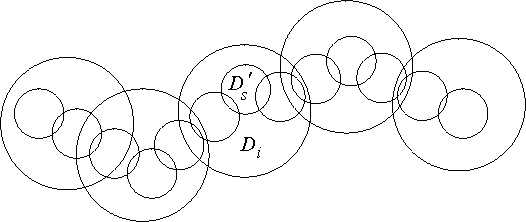The first hereditarily indecomposable
continuum has been constructed by B. Knaster in 1922. This
continuum K, discovered by Knaster, is just named the pseudo-arc or Knaster's continuum. The pseudo-arc K
is obtained as the common part of a decreasing sequence of
continua in the plane, every of which is the union of
finitely many discs, forming a chain of sets.
We
will consider chains
Let two
chains of discs ![]() and
and ![]() be given. We say that
the chain
be given. We say that
the chain ![]() refines the chain
refines the chain ![]() if each
link D's of the chain
if each
link D's of the chain ![]() is contained in the
interior of at least one link Di of the chain
is contained in the
interior of at least one link Di of the chain ![]() ,
i.e., if for every
,
i.e., if for every
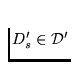 there exists a link
there exists a link
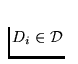 such that
such that
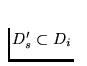 and that the
disc D's has no common points with the boundary of the
disc Di (Figure B).
and that the
disc D's has no common points with the boundary of the
disc Di (Figure B).
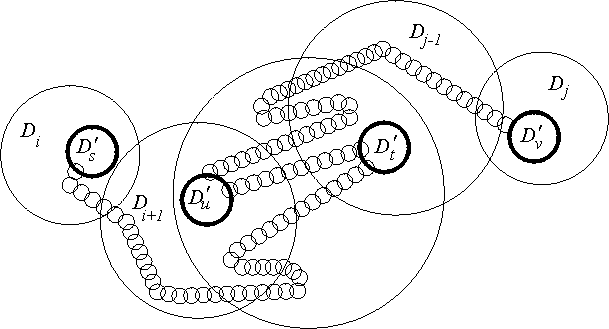
We say that the chain ![]() is crooked in the chain
is crooked in the chain ![]() if it refines
if it refines ![]() and if, for every pair of links Di and Dj of the
chain
and if, for every pair of links Di and Dj of the
chain ![]() such that
such that
| i + 2 < j, | (1) |
| (2) |
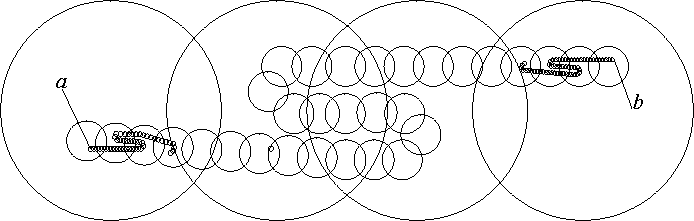
Now, let there be given
in the plane two points a and b, and an infinite
sequence
 , the
following conditions:
, the
following conditions:
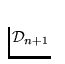 is crooked in the chain
is crooked in the chain
Thus, for example, the chain ![]() is crooked in the chain
is crooked in the chain
![]() , and the chain
, and the chain ![]() is crooked in the chain
is crooked in the chain ![]() (on
Figure D only a part of the chain
(on
Figure D only a part of the chain ![]() is presented). The foldings are
more and more condensed and they overlapped themselves.
is presented). The foldings are
more and more condensed and they overlapped themselves.
Denote by Kn the union of all links of the chain Dn. From condition
3o it follows in particular that the each next chain refines the previous
one, and therefore the continua Kn form a decreasing sequence
The Pseudo-arc K is defined as the common part of all continua
Kn, i.e.,
Let 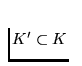 be an arbitrary continuum. To prove that the continuum
K is indecomposable it is enough to show that every continuum
be an arbitrary continuum. To prove that the continuum
K is indecomposable it is enough to show that every continuum 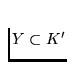 distinct from K' is nowhere dense in K'. Consider an
arbitrary point
distinct from K' is nowhere dense in K'. Consider an
arbitrary point 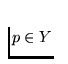 and number
and number
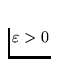 .
.
Since 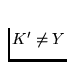 , hence there is a point
, hence there is a point
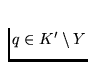 which
therefore is at a distance at least
which
therefore is at a distance at least 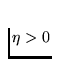 from each point
from each point 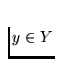 ,
where
,
where ![]() is a fixed number, independent from y. In fact, if not, then
some points of the set would be arbitrarily close to the point q, and so
the point q would belong to the closure of the set Y, which is
impossible, because the set Y is closed, and it does not contain the point
q. Let us take a natural number n so large that the inequalities are
satisfied
is a fixed number, independent from y. In fact, if not, then
some points of the set would be arbitrarily close to the point q, and so
the point q would belong to the closure of the set Y, which is
impossible, because the set Y is closed, and it does not contain the point
q. Let us take a natural number n so large that the inequalities are
satisfied
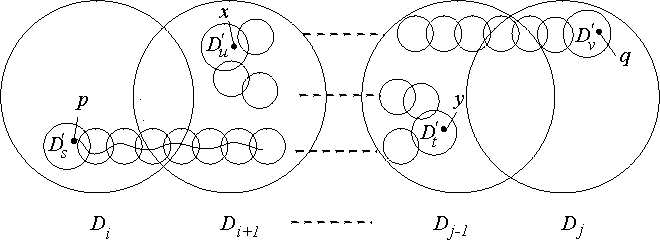
Denote by Di and Dj (with 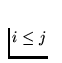 ) the links of the chain
) the links of the chain ![]() whose union contains the points p and q. Since
whose union contains the points p and q. Since 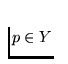 , hence
, hence
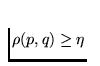 , (here
, (here ![]() means the metric in the plane) and thus
it follows that between the links Di and Dj there are at least two
links of the chain
means the metric in the plane) and thus
it follows that between the links Di and Dj there are at least two
links of the chain ![]() . Indeed, in the opposite case the links Di
and Dj would have a neighbor common link, and choosing suitable points
p' and q' in the intersections of this link with the links Di and
Dj we would have
. Indeed, in the opposite case the links Di
and Dj would have a neighbor common link, and choosing suitable points
p' and q' in the intersections of this link with the links Di and
Dj we would have
Denote by D's and D'v the links of the chain
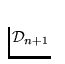 which
contain points p and q, respectively. Additionally we assume that
which
contain points p and q, respectively. Additionally we assume that
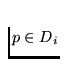 . In the opposite case, i.e. if
. In the opposite case, i.e. if 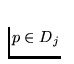 , the further part of
the proof runs in the same way (with changing of the roles of the links
Di and Dj as well as Di+1 and Dj-1).
, the further part of
the proof runs in the same way (with changing of the roles of the links
Di and Dj as well as Di+1 and Dj-1).
So,
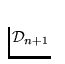 which lie between the links D's and D'v in the same order and
which satisfy the inclusions (2). The union of the links of the chain
which lie between the links D's and D'v in the same order and
which satisfy the inclusions (2). The union of the links of the chain
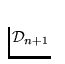 distinct from the link D'u is a not connected set (see
above) containing the point p in one component, and the point q in the
other. Since the continuum K' joins the points p and q and is
contained in the union Kn+1 of all links of the chain
distinct from the link D'u is a not connected set (see
above) containing the point p in one component, and the point q in the
other. Since the continuum K' joins the points p and q and is
contained in the union Kn+1 of all links of the chain
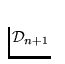 ,
hence K' must pass thru the link D'u. Thus there is a point
,
hence K' must pass thru the link D'u. Thus there is a point
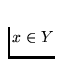 , then by the same reason as
previously for the continuum K' the continuum Y would have to pass thru
the link D't. Then there would exist a point
, then by the same reason as
previously for the continuum K' the continuum Y would have to pass thru
the link D't. Then there would exist a point
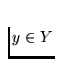 .
.
So, the point
x belongs to the set
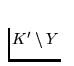 and to the link
Di+1 simultaneously. The neighbor links Di and
Di+1 have diameters less than
and to the link
Di+1 simultaneously. The neighbor links Di and
Di+1 have diameters less than ![]() , whence it
follows that
, whence it
follows that
Since ![]() was an arbitrary positive number, hence, in
this way we have proved in that there are points of the set
was an arbitrary positive number, hence, in
this way we have proved in that there are points of the set
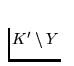 which lie arbitrarily closely to the point
p. The point p was an arbitrary point of the continuum
Y. Thus we have proved that the continuum Y is nowhere
dense in K', and the proof of hereditary indecomposability
of the continuum K is finished.
which lie arbitrarily closely to the point
p. The point p was an arbitrary point of the continuum
Y. Thus we have proved that the continuum Y is nowhere
dense in K', and the proof of hereditary indecomposability
of the continuum K is finished.
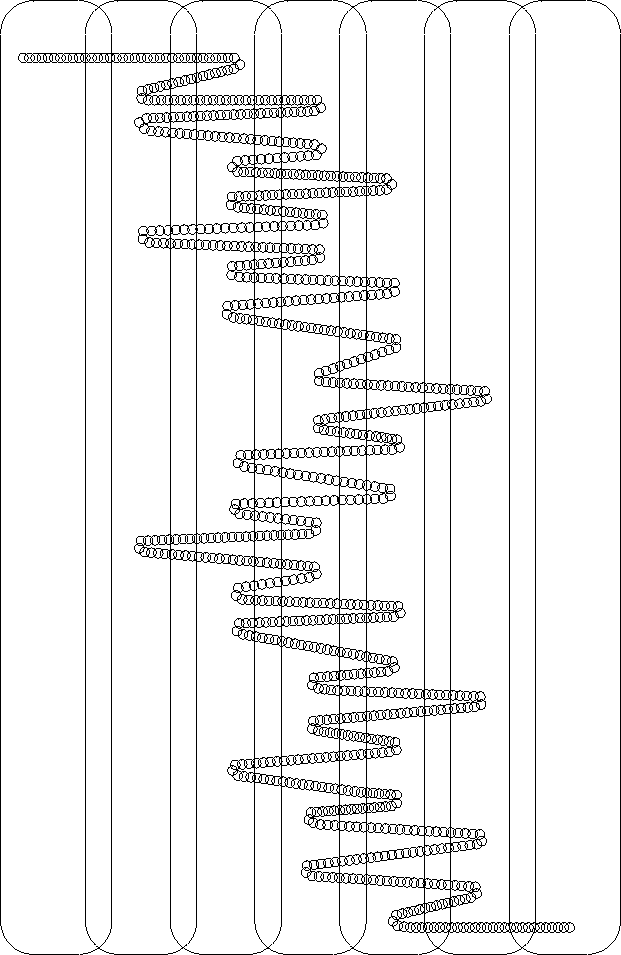
An example of a chain crooked in a chain with 7 links is on
Figure F.