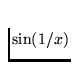 -curve
-curve
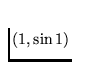 also is
a cutting. But both these continua contain arcs, which
certainly do not cut the plane. So, one can ask a question
if there exists such a cutting
also is
a cutting. But both these continua contain arcs, which
certainly do not cut the plane. So, one can ask a question
if there exists such a cutting
 that
each nondegenerate subcontinuum of X also cuts
that
each nondegenerate subcontinuum of X also cuts 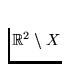 . A continuum
X is a cutting of
. A continuum
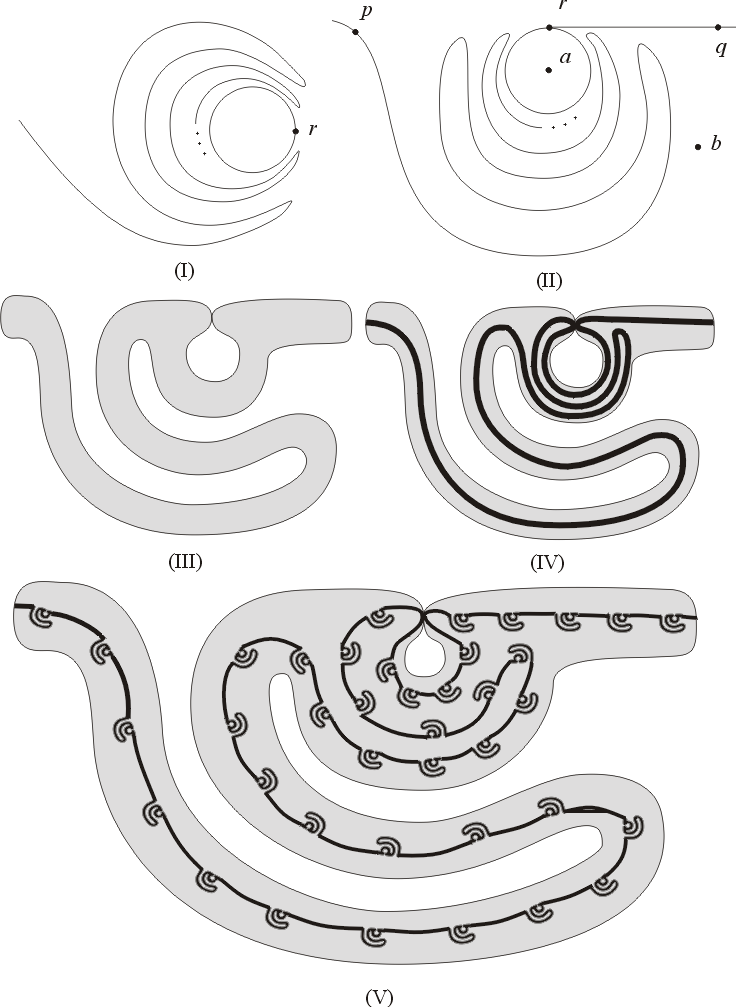
X is a cutting of 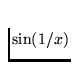 curve S and identify points (0,1) and
(0,-1) into one point r. The obtained curve (still
considered as a subset of the plane) consists of a circle
C and a sinusoidal curve approximating the circle, so it
is a cutting of the plane. If we add to the curve an arc
starting at r and having only this point in common with
the curve, we get a continuum Y being also a cutting of
the plane (namely it cuts the plane between a point a
inside the circle C and a point b lying in
curve S and identify points (0,1) and
(0,-1) into one point r. The obtained curve (still
considered as a subset of the plane) consists of a circle
C and a sinusoidal curve approximating the circle, so it
is a cutting of the plane. If we add to the curve an arc
starting at r and having only this point in common with
the curve, we get a continuum Y being also a cutting of
the plane (namely it cuts the plane between a point a
inside the circle C and a point b lying in
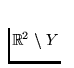 outside C) and having the property that every
subcontinuum of Y containing a point p of the sinusoidal
part of Y and a point q lying on the added arc, also
cuts the plane between a and b (see Figure A (I)-(II).).
outside C) and having the property that every
subcontinuum of Y containing a point p of the sinusoidal
part of Y and a point q lying on the added arc, also
cuts the plane between a and b (see Figure A (I)-(II).).
The same curve Y can also be obtained as the intersection of a nested sequence of plane continua. Each continuum of the sequence has the form of a long strip with one loop and finitely many zig-zags. Consecutive strips are thinner and thinner, more and more narrow, each next being inscribed in the previous one in such a way that the next loop is contained in the previous loop which also contains one more zig-zag of the next strip (see Figure A (III)-(IV)). Consequently, the number of zig-zags in the next approximation is greater than that in the previous one, so these numbers tend to infinity. The common part of the all strips is just the curve Y, while the common part of the loops is the circle C contained in Y.
The Whyburn's curve W can be obtained in a similar way, as the intersection of a nested sequence of strips in the plane, using the method called "condensation of singularities". Namely the singularity appearing in each neighborhood of C in Y is copied more and more times both in the loops as well as in the zig-zag parts of the consecutive strips. A little bit more precisely speaking, the strips are modified so that each next strip, magnifying the number of zig-zags in the loops and preserving previous loops, contains also new, smaller loops, distributed in a more and more dense manner inside the previous strip (see Figure A (V)) so that the diameters of the loops tend to zero as the number of steps of the construction tends to infinity. As a consequence of this property, for every two points p and q of the curve W one can find, in a sufficiently far approximating strip, a loop lying between these points. Roughly speaking, behavior of the curve W between p and q is such as that of the curve Y, i.e., each subcontinuum of W containing p and q cuts the plane between some points a and b determined by the mentioned loop.
The continuum W constructed is this
way has, among others, the following properties (see [1]).
1) each subcontinuum of W is a cutting of the plane, and
therefore W contains no arc; 2) each subcontinuum of W
contains a homeomorphic copy of W; 3) W is hereditarily
decomposable; and 4) W is a continuous image of the
pseudo-arc ![]() . Since neither the pseudo-arc
. Since neither the pseudo-arc ![]() nor any subcontinuum of
nor any subcontinuum of ![]() cuts the plane, this last
property shows that a hereditary anti-cutting of
cuts the plane, this last
property shows that a hereditary anti-cutting of ![]() can be continuously mapped onto a hereditary cutting.
can be continuously mapped onto a hereditary cutting.
[1] A. Lelek : On weakly chainable continua, Fund. Math. 51 (1962), 271-282.
[2] A. Lelek : Zbiory, PZWS, Warszawa 1966.
[3] G. T. Whyburn : A continuum every subcontinuum of which
separates the plane, Amer. J. Math. 52 (1930), 319-330.