



Next: Boxes Continuum
Up: New examples
Previous: Pseudo-circle
Semicircle Continuum is a nice continuum.
Let
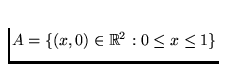 ;
;
for each 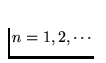 and each
and each
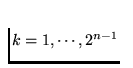 , let
, let
for each 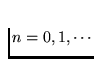 and each
and each
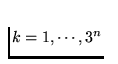 , let
, let
let
1) X is an example of an hlc continuum which is
not regular.
2) X is the union of two regular continua.
See Nadler 10.59, p.193.
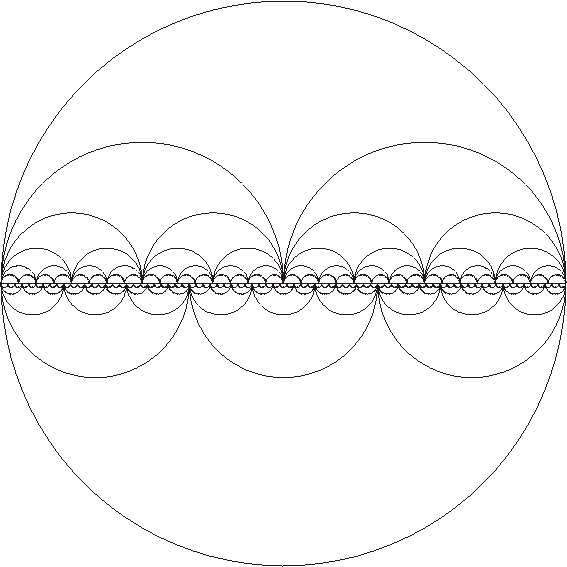
Figure (
A
)
Semicircle Continuum
Source files:
a.eps .
a.gif .
a.mws .
latex.tex .
title.txt .
Here you can
read Notes or
write to Notes.
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
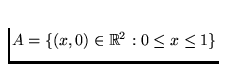 ;
;
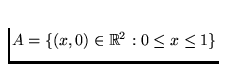 ;
;
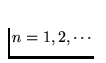 and each
and each
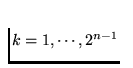 , let
, let
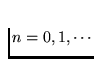 and each
and each
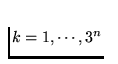 , let
, let
![\begin{displaymath}
X = A \cup \left [\bigcup_{n=1}^\infty \left (
\bigcup_{k=1}...
...}^\infty \left ( \bigcup_{k=1}^{3^{n}} C_{n,k}\right
)\right ]
\end{displaymath}](img100.gif)
