Quételetova - Dandelinova věta
Řez rotačního válce rovinou
Tato kapitola je doplněním předchozí kapitoly. Budeme se tentokrát zabývat řezy rotační válcové plochy rovinou.
Stejně jako tomu bylo u řezů rotační kuželové plochy, i v případě rotační válcové plochy dostáváme kuželosečky. Označme válcovou plochu V, její osu o a rovinu řezu \rho. Pokud je \rho tzv. směrová rovina - rovnoběžná se směrem površek plochy V, řezem budou singulární kuželosečky, a to: přímka nebo dvě navzájem rovnoběžné přímky (v obou případech se jedná o povrchové přímky válcové plochy V, viz obrázek V5.1 a), b)). Přímku dostáváme v případě, když rovina \rho je tečnou rovinou plochy V.
Obrázek V5.1: Klasifikace rovinných řezů rotační válcové plochy. Řezem je: a)jedna povrchová přímka, b) dvě rovnoběžky (povrchové přímky), c) kružnice, d) elipsa
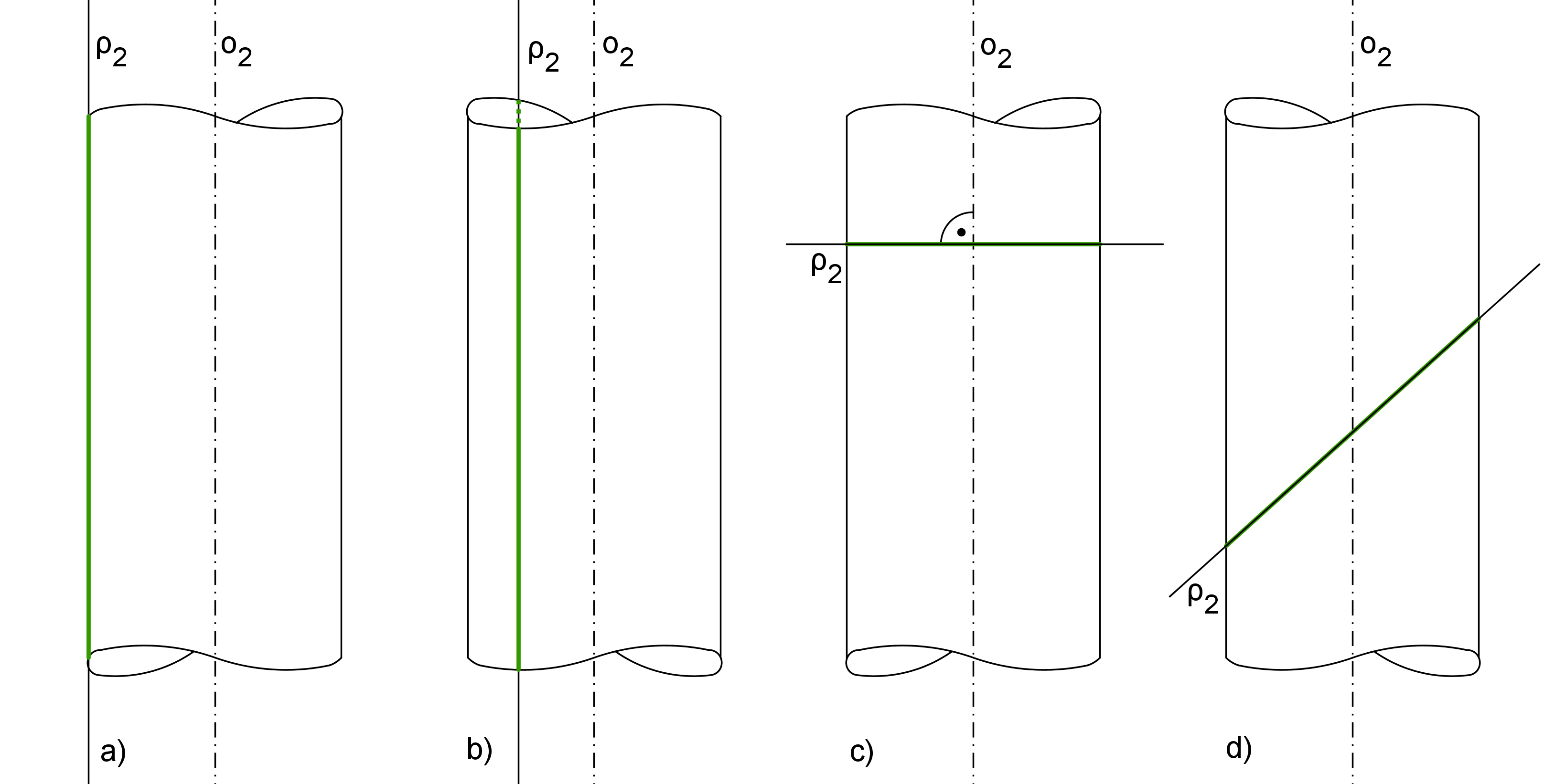
Pozn. k obrázku V5.1: Dané válcové plochy volíme tak, že mají osy o v průmětně (nárysně), rovina řezu \rho je k průmětně kolmá, zobrazuje se jako přímka. Řezy jsou částmi této přímky. Libovolná povrchová kružnice válcové plochy se zobrazuje jako úsečka kolmá k její ose. Tento způsob zobrazení bude použit i v ostatních obrázcích této kapitoly, ovšem objekty budou pro jednoduchost popisovány bez 2 v dolním indexu (což značí, že se jedná o nárys).
Pokud rovina řezu \rho není směrová, potom je řezem regulární kuželosečka a to buď kružnice nebo elipsa, viz obrázek V5.1 c), d). Vlastnosti elipsy, která je řezem rotační válcové plochy popisuje Quételetova - Dandelinova věta. (citace z: Pomykalová [11] str. 264)
Věta V5.1 (Quételet, Dandelin): Řezem rotační válcové plochy rovinou, která je kosá k ose plochy, je elipsa. Jejími ohnisky jsou dotykové body kulových ploch vepsaných válcové ploše tak, že se dotýkají roviny řezu. Střed elipsy leží na ose válcové plochy, délka její vedlejší poloosy je rovna poloměru válcové plochy.
Věta V5.1 hovoří o rovině, která je kosá k ose plochy. Poznamenejme jen, že pokud by rovina řezu \rho byla kolmá k ose plochy, potom by řezem byla kružnice. Kružnici můžeme brát jako speciální případ elipsy. Vepsané sféry by se v tomto případě dotýkaly roviny \rho ve stejném bodě - středu kružnice.
V Apletu V5.1 níže je nárys části rotační válcové plochy. Je zde zobrazena rovina \rho, jejíž polohu můžete měnit pomocí bodů A', \, B'. Změnou polohy roviny \rho se budou měnit vepsané sféry a tedy i dotykové body - ohniska elipsy řezu. Vpravo je potom skutečná velikost řezu - elipsy. Všimněte si, že "výška" = vedlejší poloosa elipsy je i přes změnu polohy roviny stejná. To proto, že je rovna poloměru válcové plochy, jak říká věta V5.1.
Aplet V5.1: Eliptický řez rotační válcové plochy; skutečný obraz řezu.
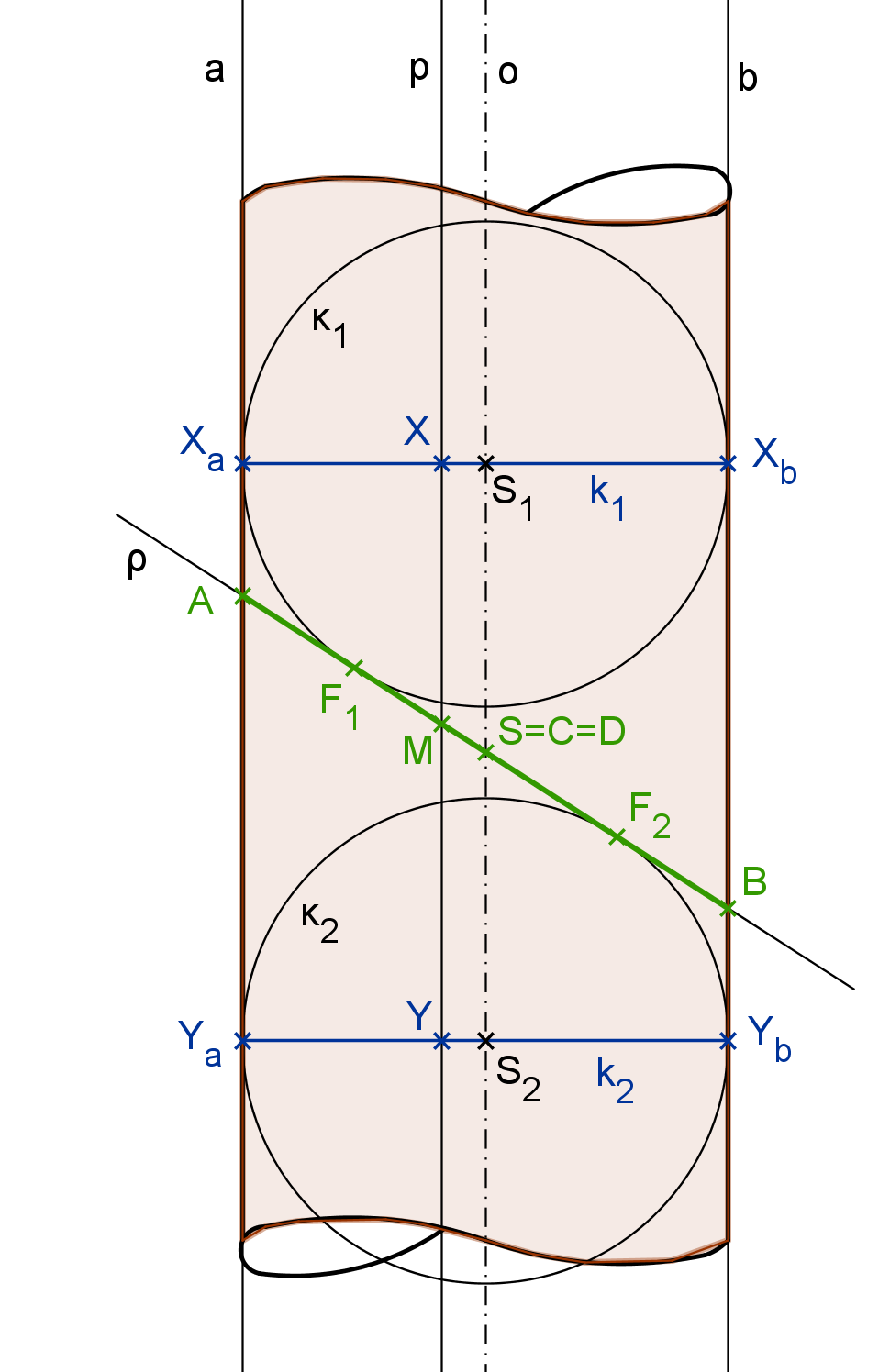
Důkaz Věty V5.1 (Quételet, Dandelin): (obrázek V5.2)
Důkaz budeme provádět obdobně jako důkaz pro eliptický řez rotační kuželové plochy.
Nechť je dána rotační válcová plocha V a rovina \rho je rovinou řezu. \rho není směrová rovina a je kosá k ose plochy o. Vepišme (podle věty V5.1) do válcové plochy V sféry \kappa_1, \, \kappa_2 tak, aby se dotýkaly i roviny \rho. Středy S_1, \, S_2 těchto sfér leží na ose válcové plochy a dotýkají se plochy V podél kružnic k_1, \, k_2. Dále označme F_1, \, F_2 body dotyku kulových ploch \kappa_1, \, \kappa_2 s rovinou \rho.
Naším úkolem je nyní dokázat, že řezem je elipsa s ohnisky F_1, \, F_2. Zvolme tedy libovolně bod řezu M a veďme jím povrchovou přímku p válcové plochy V (M \in p \, || \, o). Přímka p se dotýká sféry \kappa_1 v bodě X (X \in k_1) a druhé sféry \kappa_2 v bodě Y (Y \in k_2).
Platí: |MF_1| = |MX|, protože MF_1 i MX jsou tečny sféry \kappa_1, body F_1 a X jí náleží, tudíž jsou stejně vzdálené od bodu M. Stejně tak: |MF_2| = |MY|.
Z toho plyne: |MF_1| + |MF_2| = |MX| + |MY| = |XY| = |S_1S_2|.
Též body A, \, B jsou body řezu, a proto: |AF_1| + |AF_2| = |AX_a| + |AY_a| = |X_aY_a| = |S_1S_2|, resp. |BF_1| + |BF_2| = |BX_b| + |BY_b| = |X_bY_b| = |S_1S_2|. A protože |AF_1| = |BF_2|, dostáváme |S_1S_2| = |BF_2| + |AF_2| = |AB|.
Tímto jsme dokázali, že libovolný bod řezu má od bodů F_1, \, F_2 konstantní vzdálenost |AB| > |F_1F_2|, tudíž průnikovou křivkou je elipsa. Body A, \, B jsou hlavními vrcholy elipsy, střed S úsečky AB je jejím středem (S \in o). Vedlejší vrcholy C, \, D elipsy jsou průsečíky válcové plochy V a kolmice k úsečce AB procházející středem S a ležící v rovině \rho. Délka vedlejší poloosy je tedy rovna poloměru válcové plochy V.
Snadno zjistíme, že obráceně každý bod elipsy je také bodem řezu a tím je věta dokázána.
Obrázek V5.2: Důkaz eliptického řezu