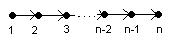
10.11.

1. Nechť G je grupa a H její podgrupa řádu 70 a K její podgrupa řádu 16. Určete počet prvků grupy G, vite-li, že |G| < 1000.
   

Podle Lagrangeovy věty musí řád podgrup H i K dělit řád grupy G, proto 70/|G| a 16/|G| a tudíž 560=nsn(70,16)/|G|. Protože |G| < 1000, máme |G| = 560.



2. Nechť G je grupa a H její podgrupa řádu 70 a K její podgrupa řádu 16. Rozhodněte, zda je G průnik H a K nutně komutativní grupa.
   

Opět použijeme Lagrangeovu větu, tentokrít pro HnK jako podgrupu grupy H i K. Velikost průniku HnK, proto musí dělit řád grupy H i K, tedy |HnK| dělí i NSD(70,16)=2. Proto je průnik HnK jednoprvková nebo dvouprvková, tedy v obou případech cyklická grupa. Protože je každá cyklická grupa komutativní, je průnik H a K nutně komutativní grupa.



3. Najděte nějakou grupu, která by měla 560 prvků a obsahovala podgrupy řádu 70 a 16.
   

Stačí, abychom vzali grupu Z₅₆₀. Její podgrupou řádu 70 je cyklická grupa < 8 > a podgrupou řádu 16 cyklická grupa < 35 >.



4. Nechť G je konečná cyklická grupa, |G|=n, a nechť k dělí n. Ukažte, že existuje právě jedna podgrupa grupy G, která má k prvků.
   

K důkazu opět využijeme charakterizace cyklických grup a tvrzení dokážeme pro (izomorfní) grupu Z_n.

Pokud k=1, je tvrzení triviální, předpokládejme, že k > 1. Položme a = n/k. Potom zřejmě

< a > = {0, a, 2a, ..., (k-1).a},

tedy |< a >| = k. Mějme nyní nějakou k-prvkovou podgrupu H. Podle Lagrangeovy věty řád grupy < h > dělí k pro každý prvek h z H, proto (k.h)mod n=0. Tudíž k.h=c.n pro vhodné celé číslo c, tedy h=c.n/k=c.a. Tím jsme ověřili, že H je částí podgrupy < a >. Protože se jedná ovšem o dvě konečné stejně velké množiny dostáváme, že H=< a >, čímž jsme ověřili jednoznačnost volby.

24.11.

5. Kolik podgrup obsahuje cyklická grupa řádu 98?
   

Využikeme předcázející úlohu: každému děliteli řádu cyklické grupy odpovídá právě jedna její podgrupa. Potřebujeme tedy jen spočítat dělitele číslo 98, kterých je 6 (tj. 1, 2, 7, 14, 49, 98).



6. Popište strukturu grupy automorfismů Aut(Z_n) grupy (Z_n, +, - ,0) pro libovolné přirozené číslo n.
   

Snadno nahlédneme, že je každý endomorfismus grupy (Z_n, +, - ,0) (tj. homomorfismus grupy do sebe) určen obrazem prvku 1 (nebo jiného generátoru), označme ho tedy k. Pro libovolné i z Z_n máme:

F_k(i) = (k.i)mod n.

Všimněme si, že každé takové zobrazení F_k je endomorfismem grupy (Z_n, +, - ,0). Zbývá nahlédnout, že F_k je automorfismus, právě když je k nesoudělné s n (tj. NSD(k,n)=1).

Je-li nejprve d = NSD(k,n) > 1, potom c=n/d je nenulový prvek Z_n a F_k(c) = (n.(k/d))mod n = 0, tedy F_k není bijekce. Předpokládejme, že NSD(k,n)=1. Pokud F_k(i)=0, potom n dělí součin i.k, to ovšem znamená, že n dělí i (neboť k a n jsou nesoudělná), tedy i=0. F_k je prosté zobrazení konečné množiny Z_n do sebe, tedy jde o bijekci.




7. Určete počet prvků grupy automorfismů Aut(G), kde G je cyklická grupa řádu 100.
   

Protože je grupa G izomorfní grupě (Z₁₀₀, +, - ,0), stačí podle výsledku předchozí úlohy spočítat prvky z Z₁₀₀ nesoudělné se stovkou, tedy určit hodnotu Eulerovy funkce na prvku 100. Prvočíelný rozklad čísla 100 je 2²5², proto dostáváme, že |Aut(G)| = |Aut(Z₁₀₀)|= f(100)= (2-1).5.(5-1).4= 40.



8. Ověřte, že pro každý prvek g konečné grupy G platí, že g^|G|=1.
   

Z popisu cyklických grup okasmžitě plyne, že g^{|< g >|} = 1. Nyní stčí použít Lagrangeovu větu a pozorování, že (g^a)^b = g^ab:

g^|G| = (g^{|< g >|})^{|G|/|< g >|} = 1^{|G|/|< g >|} = 1.



9. Dokažte, že pro každé a nesoudělné s n platí, že (a^f(n))mod n = 1, kde f je Eulerova funkce (Malá Fermatova věta).
   

Stačí vzít jako grupu G z předchozího příkladu grupu invertibillních prvků monoidu (Z_n, . , 1), tj. prvků nesoudělných s n.



10. Nechť p a s jsou permutace na S_n a nechť p(a)=b. Dokažte, že (sps^-1)(s(a)) = s(b).
    

Důkaz tvrzení je zcela přímočarý. Důležitým důsledkem je ovšem pozorování, že permutace p a sps^-1 mají stejný počet stejných cyklů, neboť jsme právě dokázali, že s [...(...ab...)...] s^-1 = ...(...s(a)s(b)...)... .



11. Mějme permutace p=(1346)(27)(589) a q=(16)(29)(345) dvě permutace z S₉. Spočítejte hodnoty pqp^-1 a qpq^-1.
    

Postupujeme podle předchozího pozorování:

[(1346)(27)(589)] [(16)(29)(345)] [(1346)(27)(589)]^-1 = (31)(75)(468),
[(16)(29)(345)] [(1346)(27)(589)] [(16)(29)(345)]^-1 =(6451)(97)(382).

12. Mějme permutace p₁=(126)(37)(458) a p₂=(12)(345)(678) dvě permutace z S₈. Rozhodněte, zda existuje permutace q s vlastností qp₁q^-1=p₂ a případně takovou permutaci q najděte.
    

Využijeme opačný postup k postupu v předchozím příkladu. Obě permutace jsou stejného typu (což je zřejmě nutná podmínka, aby permutace q existovala). Seřaďme stejnými n-cykly pod sebe, například:

(126)(37)(458)
(345)(12)(678)

Zřejmě potom permutace q=(13)(24657)(8) splňuje podmínku qp₁q^-1=p₂.



13. Ověřte, že alternující grupa na čtyřech prvcích A₄ neobsahuje žádnou podgrupu řádu 6.
    

Uvědomme si, že A₄ = {Id, (12)(34), (13)(24), (14)(23), (123), (132), (124), (142), (134), (143), (234), (243)}. Předpoládejme, že máme podgrupu H řádu alespoň 6. To určitě znamená, že H obsahuje alespoň dva trojcykly, tj. permutace tvaru (abc), bez újmy na obecnosti můžeme předpokládat, že A₄ obsahuje trojcyklus (123). Podle Lagrangeovy věty je index podgrupy H v grupě A₄ nejvýše 2. Tedy podle tvrzení z přednášky je H normální podgrupa A₄. To ovšem znamená, že p(123)p^-1 = (p(1)p(2)p(3)) leží v H pro každé p z A₄. Nyní snadno spočítáme, že

(214) = (12)(34) (123) ((12)(34))^-1,
(341) = (13)(24) (123) ((13)(24))^-1,
(432) = (14)(23) (123) ((14)(23))^-1.

Protože je H normální podgrupa, leží (214), (341) i (432) v H navíc v H leží i inverzní permutace (124), (143) a (243), tedy H obsahuje více než 6 prvků. Z Lagrangeovy věty už plyne, že |H|=12, proto H=A₄.

1.12.

14. Jakou má strukturu grupa všech symetrií čtverce D₈?
    

Nalezení množiny všech symetrií čtverce je geometricky velmi názorné a nevyžaduje další formální důkaz. Tato množina obsahuje identitu otočení o 90, 180 a 270 stupňů, osovou symetrii podle dvou diagonál a dvě osové symetrie podle spojnice středů dvou protilehlých stran. Tedy je osmiprvková.

Protože jde vlastně o permutaci vrcholů s jistými dodatečnými podmínkami, můžeme tuto grupu chápat jako podgrupu grupy všech permutací na 4 bodech. Přesněji řečeno můžeme definovat prostý homomorfismus naší grupy do S₄ (a to přesně tak, že nějak pevně očíslujeme vrcholy, a každé symetrii přiřadíme právě tu permutaci, jakou provede daná symetrie na vrcholech). Grupa D₈ je tedy izomorfní například s podgrupou {Id, (1234), (13)(24), (1432), (14)(23), (12)(34), (13), (24)} grupy S₄ (použili jsme cyklického zápisu permutací).



15. Ukažte, že pro H={Id, (13)} a K={Id, (13), (24), (13)(24)} podgrupy D₈ platí, že H je normální podgrupa K, K je normální podgrupa D₈ a H není normální v D₈.
    

Připomeňme, že D₈ můžeme chápat jako podgrupu {Id, (1234), (13)(24), (1432), (14)(23), (12)(34), (13), (24)} grupy S₄. Okamžitě z pozorování 20 můžeme nahlédnout, že (1234)(13)(1234)^-1 = (24), tedy H není normální v D₈.

Z Lagrangeovy věty dostáváme, že [K:H]=|K|/|H|=2 a [D₈:K]=|D₈|/|K|=2. Z Věty 1.39 potom plyne, že H je normální v K a K je normální v D₈.

Nechť X je množina a G grupa. Připomeňme, že působením grupy G na množině X rozumíme každý homomorfismus F grupy G do permutační grupy S(X). Místo F(g)(x) budeme psát g(x). Označme c_x = {g z G| g(x)=x}, O_x = {g(x)| g z G} a X_g = {x z X| g(x)=x}. Konečně definujme na X ekvivalenci ~ předpisem x~y, pokud existuje g z G tak, že g(x)=y.

16. Nechť grupa G působí na množině X. Dokažte, že |G|.|X/~| = Σ_{x z X} |C_x| = Σ_{g z G} |X_g|.
    

Stačí si uvědomit (s využitím Vět 1.54 a 1.29 z přednášky), že

|G|.|X/~| = |G|.Σ_{x z X} 1/|O_x| = Σ_{x z X} |G|/|O_x| = Σ_{x z X} |C_x| = Σ_{x z X} |C_x| = |{(x,g) z XxG| g(x)=x}| = Σ_{g z G} |X_g|.



17. Spočítejte kolika způsoby lze obarvit stěny krychle (bez ohledu na její polohu) pomocí n barev.
    

Nejprve definujme množinu X jako množinu všech obarvení krychle v pevné pozici (tj. přiřazujeme barvu 6 pozicím s ohledem na jejich polohu) a G grupu všech otočení krychle. Konečně otočení g přiřadí obarvení x příslušně otočení krychle g(x). Zřejmě jde o působení G na množině X. Všimněme si, že dvě obarvení z množiny X jsou ekvivalentní vzhledem k ekvivalenci ~, pokud lze jedno převést na druhé nějakým otočením krychle. To znamená, že počet všech obarvení krychle bez ohledu na její otočení je právě roven |X/~|. Využijeme dokázaného vztahu |X/~| = 1/|G| Σ_{g z G} |X_g|.

Uvědomme si, že grupa otočení G obsahuje právě 24 prvků (otočení můžeme reprezentovat zobrazením stěny na jednu z 6 stěn ve 4 pozicích, případně zobrazením jednoho vrcholu na 8 vrcholů s trojicí hran, které z něj vybíhají). Každé otočení můžeme reprezentovat jako permutaci stěn, které se k tomuto účelu očíslujeme čísly 1,...,6 (tedy grupu G chápeme jako podgrupu S₆). Konečně poznamenejme, že má-li zůstat při konkrétním otočení zachováno obarvení krychle, musí být obarvení všech stěn v jednom cyklu stejné. Tedy potřebujeme zjistit kolik cyklů každá z permutací odpovídající danému otočení obsahuje (je-li jich v permutaci g právě k, pak |X_g|=n^k). Probereme jednotlivé případy:

• 6 cyklů obsahuje pouze g=id - |X_g|= n⁶,
• 4 cykly obsahují 3 osové symetrie podle os procházejících středy protilehlých stěn, tj. g leží v {(13)(24), (13)(53), (24)(56)} - |X_g|= n⁴,
• 3 cykly obsahuje 6 otočení o 90 stupňů vpravo a vlevo podle os procházejících středy protilehlých stěn, tj. g leží v {(1234), (1432), (1635), (1536), (2645), (2546)} a 6 překlopení podle os procházejících středy protilehlých hran, tj. g leží v {(13)(64)(25), (13)(26)(45), (24)(16)(35), (24)(15)(36), (56)(14)(23), (56)(12)(34)} - |X_g|= n³,
• 2 cykly obsahuje 8 otočení o 120 stupňů vpravo a vlevo podle os procházejících protilehlými vrcholy, tj. g leží v {(164)(235), (146)(253), (126)(345), (162)(354), (145)(263), (154)(236), (125)(634), (125)(634)} - |X_g|= n².

Tedy zjistili jsme, že |X/~| = 1/24 (n⁶ + 3n⁴ + 12n³ + 8n²).



18. Určete kolika způsoby lze krychli obarvit (bez ohledu na její polohu) pomocí 3 barev.
    

Nyní stačí dosadit do odvozeného vzorečku: 1/24 (3⁶ + 3.3⁴ + 12.3³ + 8.3²)

8.12.

19. Kolik prvků má podgrupa G grupy permutací na sedmi prvcích S₇ generovaná permutacemi s=(12)(457) a p=(14)(72)?
    

    Použijeme vztah dokázaný na přednážce |G| = |C_x|O_x. Snadno zjistíme, že O₁={1, 2, 7, 5, 4}. Tedy |G| = |C₁||O₁| = 5|G₁|.
    Nyní m6eme tutéž větu aplikovat na stabilizátor G₁: Orbita tranzitivity prvku 2 v této grupě O₂={2, 7, 5, 4}, neboť psps=(254) a psssp=(47). Dále grupa (C₁)₂ obsahuje permutace psssp=(47) a s²=(475) a je nto nejvýše permutační grupa na třech prvcích. Tedy |(C₁)₂|=6 a

    |G| = 5|G₁| = 5|(G₁)₂||O₂| = 5 . 6 . 4 = 120.

20. Najděte nějakou věrnou reprezentaci grupy D₈ stupně 4.
    

Stačí využít prostého homomorfismu D₈ do S₄ a poté postupovat obdobně jako při konstrukci regulární reprezentce, tj. vzít prostý homomorfismus grupy S₄ na grupu permutačních matic.



21. Existuje pro každou cyklickou grupu její věrná reprezentace stupně 1?
    

Předně si uvědomme, že grupa regulárních matic stupně 1 je izomorfní grupě nenulových prvků tělesa s násobením. Nyní stačí, abychom pro nekonečnou cyklickou grupu Z uvažovali zobrazení

g(k) = c^k,

kde c je takové nenulové komplexní číslo, že |c| je různé od 1. Potom g je prostý homomorfismus. Pro konečnou cyklickou grupu Z_n položme a = 2.Pi/n a vezměme zobrazení

g_n(k) = (cos a + i.sin a)^k = cos(k.a) + i.sin(k.a).

Snadno nahlédneme, že i tentokrát se jedná o prostý grupový homomorfismus.

1. Nechť I jde podmnožina množiny celých čísel. Dokažte, že I je podgrupa grupy (Z, +, -, 0), právě když je I ideálem okruhu (Z, +, -, 0, . ,1).
   

Podle definice je každý ideál podgrupou aditivní grupy okruhu, takže stačí dokázat přímou implikaci. Nechť I je podgrupa a i leží v I. Pak i.k = i+...+i (k krát sčítáme) pro k kladné , i.0=0 a i.k = -(i+...+i) (|k| krát sčítáme) pro k záporné. Protože je podgrupa uzavřená na +, - i 0, leží i.k (= k.i) v I, tedy I je ideál.



2. Ověřte, že všechny ideály okruhu celých čísel jsou hlavní.

Plyne okamžitě z pozorování předchozí úlohy a dokázaného faktu, že všechny podgrupy grupy (Z, +, -, 0) jsou cyklické (tedy < k > = kZ).

15.12.

3. Rozhodněte, kolik obsahuje okruh (Z₅₀, +, -, 0, . ,1) (s počítáním modulo 50) ideálů.

Uvědomíme-li si podobně jako v předchozím příkladě, že každá podgrupa (cyklické) grupy (Z₅₀, +, -, 0) je ideálem okruhu (Z₅₀, +, -, 0, . ,1), pak zbývá spočítat všechny podgrupy cyklické grupy řádu 50, tedy stačí aplikovat pozorování ze 4. příkladu kapitoly Grupy. Protože je přirozených dělitelů čísla 50 celkem 6, je v okruhu (Z₅₀, +, -, 0, . ,1) právě 6 ideálů.



4. Rozhodněte, kolik podokruhů obsahují okruhy (Z, +, -, 0, . ,1) a (Z_n, +, -, 0, . ,1).

Protože podokruh musí obsahovat prvek 1 a zároveň musí být pogrupou aditivní grupy okruhu, obsahuje (Z, +, -, 0, . ,1) i (Z_n, +, -, 0, . ,1) pouze jediný podokruh (tedy celé Z, resp. Z_n).



5. Nechť V je vektorový prostor nad tělesem T konečné dimenze. Dokažte, že je okruh (M_n(T),+,-,(0),x,E) jednoduchý, tj. že obsahuje pouze triviální ideály.

Nechť I je nenulový ideál. Potom I obsahuje nějakou nenulovou čtvercovou matici A. Označme E_ij matici, která má všude nuly, kromě pozice na i-tém řádku a j-tém sloupci.
Nechť matice A má v i-tém řádku a j-tém sloupci nenulovou hodnotu a (z T). Potom

a^-1E_ki . A . E_jk = E_kk leží v I,

neboť I je oboustranný ideál (tj. je uzavřený na násobení z leva i z prava libovolným prvkem). Zároveň i součet

E₁₁ + E₂₂ + . . . + E_nn = E leží v I.

Tedy I obsahuje jednotkovou matici E, proto I=M_n(T). Ověřili jsme, že Maticový okruh obsahuje pouze dva oboustranné ideály {0} a M_n(T).



6. Nechť V vektorový prostor dimenze n nad tělesem T. Ověřte, že okruhy (End(V), +, -, 0, . , Id) a (M_n(T), +, -, 0_n, . , E_n) jsou izomorfní.

Zvolme nějakou bázi B prostoru V. Ze základních tvrzení pro matice homomorfismů z přednášky lineární algebry plyne, že zobrazení, které každému endomorfismu F přiřadí [F]_BB jeho matici vzhledem k bázi B je hledaným okruhovým izomorfismem.



7. Nechť V je konečnědimenzionální vektorový prostor nad tělesem T. Rozhodněte, zda je okruh (End(V),+,-,0, . ,,Id)) jednoduchý.

Použijeme-li tvrzení předchozích dvou příkladů, vidíme, že okruh (End(V),+,-,0, . ,,Id)) má stejné algebraické vlastnosti jako maticový okruh (M_n(T), +, -, 0_n, . , E_n) pro n=dim(V), tedy je jednoduchý.

5.1.

Označme < TA_n > algebru cest nad tělesem T grafu:

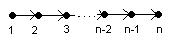
Dále označme < KT > (tzv Kronnekerovu) algebru cest nad tělesem T grafu:

8. Určete T-dimenze algebry < TA_n > a < KT >

Víme, že algebra cest je vektorový prostor s bazí danou všemi orientovanými cestami. Tedy potřebujeme spočítat orientované cesty. Snadno tedy nahlédneme (a nezapomeneme při tom na cesty délky 0, tj. všechny vrcholy grafu), že:

dim_T < TA_n > = |{(i,j)| -1 < i-1 < j < n+1}| = n.(n+1)/2,
dim_T < KT > = |{1, 2, a, b}| = 4.



9. Určete T-dimenze hlavních pravých ideálů 2< KT >, b< KT > a levých ideálů < KT >2 < KT >a algebry < KT >.

Předně si uvědomme, že každý pravý i levý ideál algebry cest je uzavřený na násobení prevkem t1, kde t je libovolný prvek tělesa T a 1 je jednička dané algebry cest (tedy v našem případě máme formální sumu t.1= t.1 + t.2+ 0.a + 0.b). To znamená, že pravé i levý ideály jsou podprostory algebry chápané jako vektorový prostor.

Zbývá abychom si uvědomili, že hlavní ideály tvaru c< KT > pro cestu c mají bázi tvořenou právě všemi cestami, kterí začínají cestou c a podbně bázi levého ideálu < KT >c tvoří cesty, které končí cestou c.

Tedy 2< KT > = < 2 >, b< KT > = < b > a < KT >2 = < 2, a, b > a < KT >a = < a >. Což znamená, že dim_T 2< KT > = dim_T b< KT > = dim_T < KT >a = 1 a dim_T < KT >2 = 3.

12.1.

10. Dokažte, že K(T) není izomorfní okruhu M₂(T).

Stačí si uvědomit, že M₂(T) je jednoduchý okruh (viz úloha 4), zatímco například podprostor < 1, 2, a> je netriviální ideál okruhu K(T), tedy K(T) jednoduchý není.



11. Ověřte, že algebra K(T) je izomorfní podokruhu maticového okruhu
    

    {

    a 0 c 0 0 a 0 d 0 0 b 0 0 0 0 b

    | a,b,c,d z T }.

Nejprve definujeme na bázi homomorfismus F vektorových prostorů, u něhož podobně jako v příkladu 15 dokážeme, že je homomorfismem algeber:

F(1) =

0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1

,   F(2) =

1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0

,   F(a) =

0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0

,   F(b) =

0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0

.

Vn bude v následujícím značit druhou odmocninu čisla n.

12. Ověřte, že Q[V2]={a+bV2; a,b ze Q} je podokruh okruhu reálných čísel.

Stačí si uvědomit, že (a+bV2).(c+dV2) = (ac+2bd) + (bc+ad)V2 (a+bV2)+(c+dV2) = (a+c) + (b+d)V2, dále, že -(a+bV2) = -a+(-b)V2 a 0 i 1 leží v Q[V2]. Tedy Q[V2] je uzavřen na všechny operace okruhu reálných čísel a je to tudíž podokruh.



13. Popište všechny ideály okruhu Q[V2] z předchozí úlohy.

Stačí si uvědomit, že v Q[V2] ke každému nenulovému prvku najdeme inverzní prvek, tedy, že Q[V2] je těleso. Vidíme, že pro každé nenulové a + bV2 je i a²-2b² nenulové a

(a + bV2).(a/(a²-2b²) + b/(2b²-a²)) = 1.

Je-li okruh tělesem potom má podle Věty 2.12 z přednášky jen triviální ideály.



14. Dokažte, že podokruh Q[V3]={a+bV3; a,b ze Q} okruhu reálných čísel a okruh Q racionálních čísel nejsou izomorfní okruhy.

Mějme libovolný prostý homomorfismus G okruhu Q do okruhu Q[V3]. Pak G(3)=G(1+1+1)=G(1)+G(1)+G(1)=3. V okruhu Q[V3] samozřejmě platí, že (V3)²=3. Nechť G je homomorfismus na. Pak by musel existovat prvek a z Q, pro nějž G(a)=V3, a proto G(a²)=G(a)²=3. Tedy jsme dostali, že a²=3 pro nějaké racionální číslo a. To je ovšem spor. Okruhy Q a Q[V3] nejsou izomorfní.



15. Dokažte, že okruhy Z[V3]={a+bV3; a,b ze Z} a Z[V5]={a+bV5; a,b ze Z} nejsou izomorfní.

Můžeme uvažovat obdobně jako v předchozí úloze. Kdyby existoval izomorfismus Z[V3] a Z[V5]. Museli bychom najít v okruhu Z[V3] odmocninu 5 a v okruhu Z[V5] odmocninu 3.



16. Popište všechny prvoideály okruhu celých čísel.

Víme, že všechny ideály okruhu Z jsou hlavní, tedy tvaru nZ, kde n je nezáporné celé číslo. Je-li n=0, zřejmě je nZ prvoideál. Je-li n prvočíslo a x.y leží v nZ, potom n/x.y, a proto n/x (tedy x leží v nZ) nebo n/y (tedy y leží v nZ). Je-li naopak n složené tj. n=a.b pro a > 1 a b > 1, pak a.b leží v nZ a a ani b v nZ neleží.

Zjistili jsme, že nZ je prvoideál právě tehdy, když je n prvočíslo nebo 0.



17. Popište všechny prvoideály okruhu reálných polynomů.

Předně poznamenejme, že každý ideál okruhu R[x] je hlavní (důkaz necháme na 2. semestr přednášky, kdy ukážete, že Eukleidův obor je nutně oborem hlavních ideálů), tedy tvaru pR[x]. Pro p=0, je zřejmě příslušný hlavní ideál prvoideálem.

Nechť a.b leží v pR[x], tedy p/a.b. Je-li st(p)=1, pak p/a (tedy a leží v pR[x]) nebo p/b (proto b leží v pR[x]). Pokud je st(p)=2 a p nemá žádný reálný kořen, má polynom p komplexní vzájemně komplexně sdružené kořeny u a v. Z předpokladu p/a.b plyne, že kořen u (a proto i v) má buď polynom a nebo polynom b, což znamená, že p/(x-2.Re(u)+|u|²)/a nebo p/(x-2.Re(u)+|u|²)/b.

Má-li p reálné kořeny r, s (buď různé nebo násobností 2) pak p=c(x-r).(x-s), kde c je nenulové reálné číslo a c(x-r) ani (x-s) neleží v pR[x], proto v takovém případě pR[x] není prvoideál. Konečně polynom stupně většího než 2, který nemá reálné kořeny má dvojici komplexně sdružených kořenů u a v, proto můžeme p napsat jako součin (x-2.Re(u)+|u|²).u, kde u je reálný polynom kladného stupně. Tedy ani tentokrát pR[x] není prvoideál.

Zjistili jsme, že pR[x]) je prvoideál právě tehdy, když je p polynom stupně 1, polynom stupně 2 bez reálných kořenů nebo polynom 0.