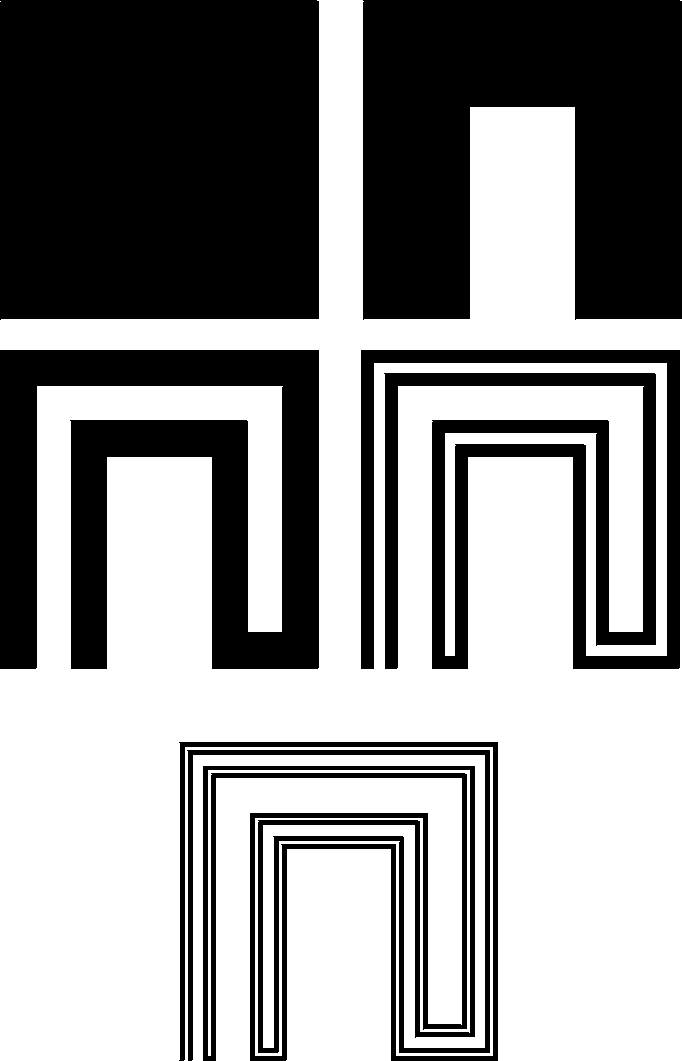



Next: Cantor Interaction
Up: New examples
Previous: M-Continuum
The Buckethandle is created from the
Cantor Ternary Set C with this procedure:
(i) we join any two points a and b in C
symmetric with respect to 1/2 with a semicircle in
the upper half plane with the centre in (1/2,0),
(ii) we join any two points of C in the interval
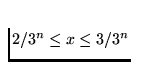 ,
, 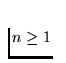 , with a semicircle
with the centre in
, with a semicircle
with the centre in
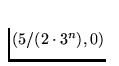 in the lower
half plane.
This continuum is often called the
Knaster's Buckethandle continuum
(see Figure (A)).
in the lower
half plane.
This continuum is often called the
Knaster's Buckethandle continuum
(see Figure (A)).
This kind of curiosities in continuum theory is connected
with common boundary of several plane regions. In 1904 A.
Schönflies started to publish a sequence of papers
[6] which became an important step in development of
continuum theory. Relying heavily on intuition, he claimed
that there do not exist three regions in the plane with
common boundary. The claim was refused by L. E. J. Brouwer
in 1910 [1] who constructed continua which are common
boundary of three regions and showed that they are
indecomposable, i.e., such continua X that there are no
nonempty proper subcontinua A and B of X with 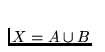 . The first example of such a continuum was given by
Brouwer in 1910 (see Figure B, where the first several steps
of his construction, simplified by Z. Janiszewski
(1888-1920) [2, p. 114] are presented). Finally in
1922 B. Knaster (1893-1980) gave a nice description of this
continuum (with the first full proof of its
indecomposability) in [3, p. 209-210]. Now the
continuum is referred to as the simplest indecomposable
continuum, or the horse-shoe continuum, or the B-J-K
continuum (for Brouwer, Janiszewski and Knaster).
. The first example of such a continuum was given by
Brouwer in 1910 (see Figure B, where the first several steps
of his construction, simplified by Z. Janiszewski
(1888-1920) [2, p. 114] are presented). Finally in
1922 B. Knaster (1893-1980) gave a nice description of this
continuum (with the first full proof of its
indecomposability) in [3, p. 209-210]. Now the
continuum is referred to as the simplest indecomposable
continuum, or the horse-shoe continuum, or the B-J-K
continuum (for Brouwer, Janiszewski and Knaster).
Finally the common boundary problem of plane domains has
been solved in 1928 by K. Kuratowski (1896-1980) who proved
in [4] and [5] that every plane continuum
which is the common boundary of n open domains either is
indecomposable or is the union of two indecomposable
continua whenever 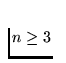 , and when n = 2 it either is "monostratic" or has a natural "cyclic
structure" in the sense that it is built up from layers naturally ordered in
the same way as the individual points of the circle.
, and when n = 2 it either is "monostratic" or has a natural "cyclic
structure" in the sense that it is built up from layers naturally ordered in
the same way as the individual points of the circle.
We can obtain a homeomorphic copy of the buckethandle
continuum using the inverse limit
where for each 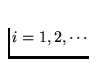 let Xi=[0,1] and
fi(t)=2t for
let Xi=[0,1] and
fi(t)=2t for
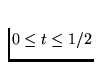 and fi(t)=-2t+2
for
and fi(t)=-2t+2
for
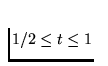 .
We can find more in [65, p.22] and
[55, p.205].
[1] L. E. J. Brouwer : Zur Analysis Situs, Math. Ann.
68(1910), 422-434.
[2] Z. Janiszewski: Sur les continus irréductibles entre deux points,
Journal de l'Ecole Polytechnique (2) 16(1912), 79-170.
[3] K. Kuratowski: Théorie des continus irréductibles entre deux points
I, Fund. Math. 3(1922), 200-231.
[4] K. Kuratowski: Sur les coupures irréductibles du
plan, Fund. Math. 6(1924), 130-145.
[5] K. Kuratowski: Sur la structure des frontières communes à deux
regions, Fund. Math. 12(1928), 20-42.
[6] A. Schönflies: Beirträge zur Theorie der Punktmengen
I, Math. Ann. 58(1904), 195-244;
II 59(1904), 129-160;
III 62(1906), 286-236.
.
We can find more in [65, p.22] and
[55, p.205].
[1] L. E. J. Brouwer : Zur Analysis Situs, Math. Ann.
68(1910), 422-434.
[2] Z. Janiszewski: Sur les continus irréductibles entre deux points,
Journal de l'Ecole Polytechnique (2) 16(1912), 79-170.
[3] K. Kuratowski: Théorie des continus irréductibles entre deux points
I, Fund. Math. 3(1922), 200-231.
[4] K. Kuratowski: Sur les coupures irréductibles du
plan, Fund. Math. 6(1924), 130-145.
[5] K. Kuratowski: Sur la structure des frontières communes à deux
regions, Fund. Math. 12(1928), 20-42.
[6] A. Schönflies: Beirträge zur Theorie der Punktmengen
I, Math. Ann. 58(1904), 195-244;
II 59(1904), 129-160;
III 62(1906), 286-236.

Figure (
A
)
Buckethandle
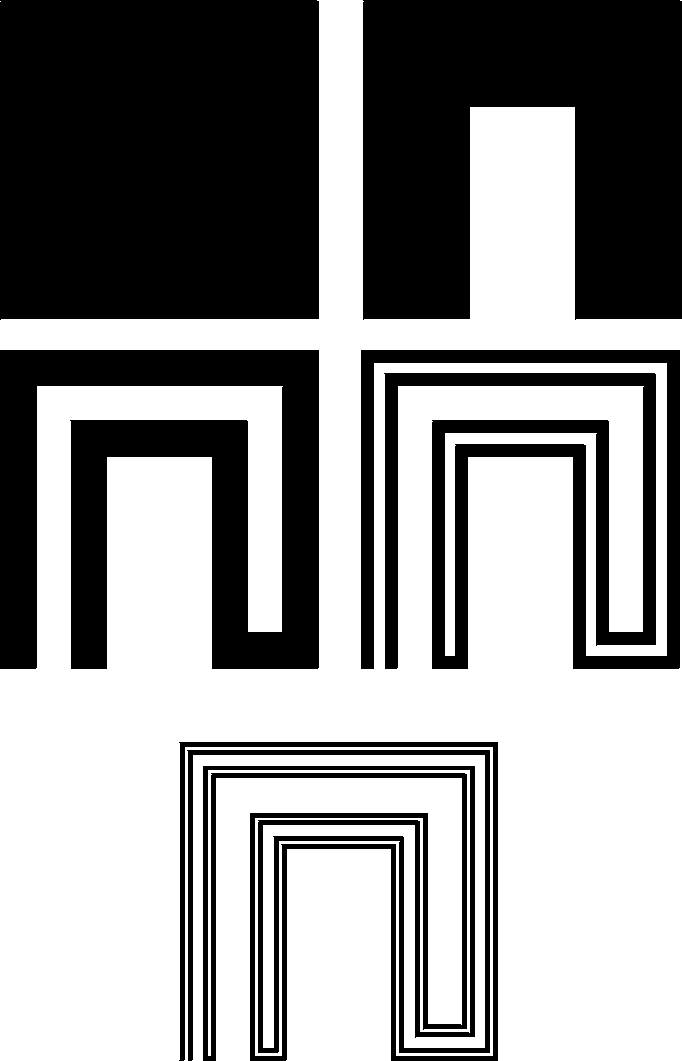
Figure (
B
)
several steps in the construction of the
Buckethandle
Source files:
a.eps .
a.gif .
b.eps .
b.gif .
b.txt .
example.htm .
figurea.mws .
figureb.cdr .
latex.tex .
title.txt .
Here you can
read Notes or
write to Notes.




Next: Cantor Interaction
Up: New examples
Previous: M-Continuum
Janusz J. Charatonik, Pawel Krupski and Pavel Pyrih
2001-02-21
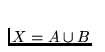 . The first example of such a continuum was given by
Brouwer in 1910 (see Figure B, where the first several steps
of his construction, simplified by Z. Janiszewski
(1888-1920) [2, p. 114] are presented). Finally in
1922 B. Knaster (1893-1980) gave a nice description of this
continuum (with the first full proof of its
indecomposability) in [3, p. 209-210]. Now the
continuum is referred to as the simplest indecomposable
continuum, or the horse-shoe continuum, or the B-J-K
continuum (for Brouwer, Janiszewski and Knaster).
. The first example of such a continuum was given by
Brouwer in 1910 (see Figure B, where the first several steps
of his construction, simplified by Z. Janiszewski
(1888-1920) [2, p. 114] are presented). Finally in
1922 B. Knaster (1893-1980) gave a nice description of this
continuum (with the first full proof of its
indecomposability) in [3, p. 209-210]. Now the
continuum is referred to as the simplest indecomposable
continuum, or the horse-shoe continuum, or the B-J-K
continuum (for Brouwer, Janiszewski and Knaster).
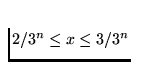 ,
, 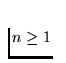 , with a semicircle
with the centre in
, with a semicircle
with the centre in
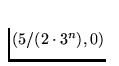 in the lower
half plane.
This continuum is often called the
Knaster's Buckethandle continuum
(see Figure (A)).
in the lower
half plane.
This continuum is often called the
Knaster's Buckethandle continuum
(see Figure (A)).
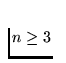 , and when n = 2 it either is "monostratic" or has a natural "cyclic
structure" in the sense that it is built up from layers naturally ordered in
the same way as the individual points of the circle.
, and when n = 2 it either is "monostratic" or has a natural "cyclic
structure" in the sense that it is built up from layers naturally ordered in
the same way as the individual points of the circle.
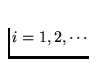 let Xi=[0,1] and
fi(t)=2t for
let Xi=[0,1] and
fi(t)=2t for
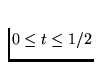 and fi(t)=-2t+2
for
and fi(t)=-2t+2
for
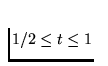 .
We can find more in [65, p.22] and
[55, p.205].
[1] L. E. J. Brouwer : Zur Analysis Situs, Math. Ann.
68(1910), 422-434.
[2] Z. Janiszewski: Sur les continus irréductibles entre deux points,
Journal de l'Ecole Polytechnique (2) 16(1912), 79-170.
[3] K. Kuratowski: Théorie des continus irréductibles entre deux points
I, Fund. Math. 3(1922), 200-231.
[4] K. Kuratowski: Sur les coupures irréductibles du
plan, Fund. Math. 6(1924), 130-145.
[5] K. Kuratowski: Sur la structure des frontières communes à deux
regions, Fund. Math. 12(1928), 20-42.
[6] A. Schönflies: Beirträge zur Theorie der Punktmengen
I, Math. Ann. 58(1904), 195-244;
II 59(1904), 129-160;
III 62(1906), 286-236.
.
We can find more in [65, p.22] and
[55, p.205].
[1] L. E. J. Brouwer : Zur Analysis Situs, Math. Ann.
68(1910), 422-434.
[2] Z. Janiszewski: Sur les continus irréductibles entre deux points,
Journal de l'Ecole Polytechnique (2) 16(1912), 79-170.
[3] K. Kuratowski: Théorie des continus irréductibles entre deux points
I, Fund. Math. 3(1922), 200-231.
[4] K. Kuratowski: Sur les coupures irréductibles du
plan, Fund. Math. 6(1924), 130-145.
[5] K. Kuratowski: Sur la structure des frontières communes à deux
regions, Fund. Math. 12(1928), 20-42.
[6] A. Schönflies: Beirträge zur Theorie der Punktmengen
I, Math. Ann. 58(1904), 195-244;
II 59(1904), 129-160;
III 62(1906), 286-236.