Derivace

Monotónnost tabulkovou metodou

V této podkapitole se naučíte nalézat intervaly monotónnosti pro různé funkce tabulkovou metodou. Platí zde předpoklady uvedené v podkapitole Předpoklady, kde je také vysvětlen pojem interval spojitosti, který se v celé této podkapitole využívá.

Nejprve je uvedena teorie a pak příklady a úlohy.

Teoretická část

Definice

Je-li funkce \(f\) definovaná v nějakém okolí bodu \(x_0\) a platí-li, že \(f^{\prime}(x_0) = 0\), pak se \(x_0\) nazývá stacionární bod funkce \(f\).

Věta

Je-li každé \(x_0\) z otevřeného intervalu \((a,b)\) stacionárním bodem funkce \(f\), potom je \(f\) na tomto intervalu konstantní.

Naopak: Je-li \(f\) na otevřeném intervalu \((a,b)\) konstantní, pak je každé \(x_0\) z tohoto intervalu stacionárním bodem funkce \(f\).

Věta

Má-li funkce \(f\) v každém bodě otevřeného intervalu \((a,b)\) kladnou derivaci, je v tomto intervalu rostoucí.

Má-li ji v každém bodě zápornou, je v tomto intervalu klesající.

Věta

Má-li funkce \(f\) v každém bodě otevřeného intervalu \((a,b)\) nenulovou derivaci, pak tam má tato derivace stále stejné znaménko. To znamená, že je funkce \(f\) na tomto intervalu monotónní.

Tabulková metoda pro určování intervalů monotónnosti:
Tisková verze je k dispozici >zde<.

Nejprve stanovíme intervaly spojitosti dané funkce. Tyto intervaly jsou vysvětleny v podkapitole Předpoklady. Mohou být otevřené, polouzavřené i uzavřené. U funkcí, které budeme zkoumat, platí, že sjednocením těchto intervalů dostaneme jejich definiční obor.
Vypočítáme derivaci funkce.
Stanovíme body z intervalů spojitosti, ve kterých není derivace definována, a stacionární body.
Pro každý interval spojitosti sestavíme samostatnou tabulku podle následujících dvou bodů.
Každý interval spojitosti dále rozdělíme pomocí krajních bodů, pokud je obsahuje, stacionárních bodů a bodů, v nichž není derivace definována, na otevřené intervaly, a tyto body a intervaly uvedeme do záhlaví příslušné tabulky.
Pro každý interval v záhlaví tabulky otestujeme v jednom libovolném bodě tohoto intervalu znaménko derivace, a podle přechozích vět stanovíme, zda je tam funkce rostoucí nebo klesající. To uvedeme v tabulce.
V závislosti na situaci případně využijeme následující větu:

Věta

Nechť je funkce spojitá na otevřeném intervalu \((a,b)\) a nechť \(c \in (a,b)\). Pokud je funkce rostoucí na intervalech \((a,c)\) a \((c,b)\), pak je rostoucí i na intervalu \((a,b)\). Pokud je funkce klesající na intervalech \((a,c)\) a \((c,b)\), pak je klesající i na intervalu \((a,b)\).

Je-li funkce monotónní na otevřeném intervalu \((a,b)\) a spojitá na intervalu \( \langle a,b)\), pak je monotónní na intervalu \( \langle a,b)\). Obdobně pro interval \((a,b \rangle \).

Je-li funkce monotónní na otevřeném intervalu \((a,b)\) a spojitá na intervalu \( \langle a,b \rangle \), pak je monotónní na intervalu \( \langle a,b \rangle \).

Příklady a úlohy

Příklad 1

Určete intervaly monotónnosti funkce \(f: y = x^2 - 4x\).

Řešení

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = 2x - 4\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(2x - 4 = 0\)): \(2\).
Tabulka:

\((-\infty, 2)\)	\(2\)	\((2, +\infty)\)
\(f^{\prime}(1) = -2 \lt 0\) klesající		\(f^{\prime}(3) = 2 \gt 0\) rostoucí

Závěr: Funkce \(f\) je klesající na intervalu \((-\infty, 2 \rangle \) a rostoucí na intervalu \( \langle 2, +\infty)\).

Úloha 1

Určete intervaly monotónnosti funkce \(f: y = x^2 + 4x + 3\).

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = 2x + 4\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Tabulka:

\((-\infty, -2)\)	\(-2\)	\((-2, +\infty)\)
		\(f^{\prime}(-1) = 2 \gt 0\) rostoucí

Závěr:

Příklad 2

Určete intervaly monotónnosti funkce \(f: y = -x^3 + 3x - 2\).

Řešení

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = -3x^2 + 3\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(-3x^2 + 3 = 0\)): \(-1; 1\).
Tabulka:

\((-\infty, -1)\)	\(-1\)	\((-1, 1)\)	\(1\)	\((1, +\infty)\)
\(f^{\prime}(-2) = -9 \lt 0\) klesající		\(f^{\prime}(0) = 3 \gt 0\) rostoucí		\(f^{\prime}(2) = -9 \lt 0\) klesající

Závěr: Funkce \(f\) je klesající na intervalu \((-\infty, -1 \rangle \) a na intervalu na intervalu \( \langle 1, +\infty)\) a rostoucí na intervalu \( \langle {-1}, 1 \rangle \).

Úloha 2

Určete intervaly monotónnosti funkce \(f: y = x^3 - 3x^2 + 2\).

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = 3x^2 - 6x\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Tabulka:

\((-\infty, 0)\)	\(0\)	\((0, 2)\)	\(2\)	\((2, +\infty)\)
\(f^{\prime}(-1) = 9 \gt 0\) rostoucí		\(f^{\prime}(1) = -3 \lt 0\) klesající		\(f^{\prime}(3) = 9 \gt 0\) rostoucí

Závěr:

Příklad 3

Určete intervaly monotónnosti funkce \(f: y = \Large\frac{3x^4-8x^3}{12}\).

Řešení

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = x^3 - 2x^2\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(x^3 - 2x^2 = 0\)): \(0; 2\).
Tabulka:

\((-\infty, 0)\)	\(0\)	\((0, 2)\)	\(2\)	\((2, +\infty)\)
\(f^{\prime}(-1) = -3 \lt 0\) klesající		\(f^{\prime}(1) = -1 \lt 0\) klesající		\(f^{\prime}(3) = 9 \gt 0\) rostoucí

Závěr: Funkce \(f\) je klesající na intervalu \((-\infty, 2 \rangle \) a rostoucí na intervalu \( \langle 2, +\infty)\).

Úloha 3

Určete intervaly monotónnosti funkce \(f: y = \Large\frac{3x^4+4x^3}{12}\).

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = x^3 + x^2\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Tabulka:

\((-\infty, -1)\)	\(-1\)	\((-1, 0)\)	\(0\)	\((0, +\infty)\)
				\(f^{\prime}(1) = 2 \gt 0\) rostoucí

Závěr:

Úloha 4

Určete intervaly monotónnosti funkce \(f: y = (x-6)^3 + 12\).

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = 3(x-6)^2\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Tabulka:

\((-\infty, 6)\)	\(6\)	\((6, +\infty)\)
\(f^{\prime}(5) = 3 \gt 0\) rostoucí		\(f^{\prime}(7) = 3 \gt 0\) rostoucí

Závěr:

Příklad 4

Určete intervaly monotónnosti funkce \(f: y = e^x(x^2-3x+1)\).

Řešení

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = e^x(x^2-x-2)\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(x^2-x-2 = 0\)): \(-1; 2\).
Tabulka:

\((-\infty, -1)\)	\(-1\)	\((1, 2)\)	\(2\)	\((2, +\infty)\)
\(f^{\prime}(-2) = 4e^{-2} \gt 0\) rostoucí		\(f^{\prime}(0) = -2 \lt 0\) klesající		\(f^{\prime}(3) = 4e^3 \gt 0\) rostoucí

Závěr: Funkce \(f\) je rostoucí na intervalu \((-\infty, -1 \rangle \) a na intervalu \( \langle 2, +\infty)\) a klesající na intervalu \( \langle {-1}, 2 \rangle \).

Úloha 5

Určete intervaly monotónnosti funkce \(f: y = e^{-x}(-x^2+2x-1)\).

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = e^{-x}(x^2-4x+3)\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Tabulka:

\((-\infty, 1)\)	\(1\)	\((1, 3)\)	\(3\)	\((3, +\infty)\)
\(f^{\prime}(0) = 3 \gt 0\) rostoucí

Závěr:

Příklad 5

Určete intervaly monotónnosti funkce \(f: y = \Large\frac{x^2-4x+4}{x+1}\).

Řešení

Čitatel v předpisu zadané funkce lze vydělit jmenovatelem. Dostaneme, že \(y = -5 + x + \Large\frac{9}{x+1}\).

Intervaly spojitosti: \((-\infty, -1)\) a \((-1, +\infty)\).
Derivace: \(f^{\prime}(x) = 1-\Large\frac{9}{(x+1)^2}\).
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(1-\Large\frac{9}{(x+1)^2}\normalsize = 0\)): \(-4; 2\).
Dvě tabulky: jedna pro interval \((-\infty, -1)\) a druhá pro interval \((-1, +\infty)\).

\((-\infty, -4)\)	\(-4\)	\((-4, -1)\)
\(f^{\prime}(-5) = \frac{7}{16} \gt 0\) rostoucí		\(f^{\prime}(-2) = -8 \lt 0\) klesající

\((-1, 2)\)	\(-2\)	\((2, +\infty)\)
\(f^{\prime}(0) = -8 \lt 0\) klesající		\(f^{\prime}(3) = \frac{7}{16} \gt 0\) rostoucí

Závěr: Funkce \(f\) je rostoucí na intervalu \((-\infty, -4 \rangle \) a na intervalu \( \langle 2, +\infty)\) a klesající na intervalu \( \langle {-4}, -1)\) a na intervalu \(({-1}, 2 \rangle \).

Úloha 6

Určete intervaly monotónnosti funkce \(f: y = \Large\frac{-x^2-4}{x}\).

Intervaly spojitosti: \((-\infty, 0)\) a \((0, +\infty)\).
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Dvě tabulky:

\((-\infty, -2)\)	\(-2\)	\((-2, 0)\)
		\(f^{\prime}(-1) = 3 \gt 0\) rostoucí

\((0, 2)\)	\(2\)	\((2, +\infty)\)
\(f^{\prime}(1) = 3 \gt 0\) rostoucí

Závěr:

Příklad 6

Určete intervaly monotónnosti funkce \(f: y = e^{-x}+\Large\frac{1}{x}\).

Řešení

Intervaly spojitosti: \((-\infty, 0)\) a \((0, +\infty)\).
Derivace: \(f^{\prime}(x) = -e^{-x}-\Large\frac{1}{x^2}\).
Poznámka: Všimněte si, že hodnoty výrazů \(e^{-x}\) a \(\Large\frac{1}{x^2}\) jsou pro \(x \neq 0\) vždy kladné.
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(-e^{-x}-\Large\frac{1}{x^2}\normalsize = 0\)): žádné.
Dvě tabulky: jedna pro interval \((-\infty, 0)\) a druhá pro interval \((0, +\infty)\).

\((-\infty, 0)\)
\(f^{\prime}(-1) = -e-1 \lt 0\) klesající

\((0, +\infty)\)
\(f^{\prime}(1) = -e^{-1}-1 \lt 0\) klesající

Závěr: Funkce \(f\) je klesající na intervalu \((-\infty, 0)\) a na intervalu \((0, +\infty)\).

Úloha 7

Určete intervaly monotónnosti funkce \(f: y = x-\Large\frac{2}{x+1}\).

Intervaly spojitosti: \((-\infty, -1)\) a \((-1, +\infty)\).
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Dvě tabulky:

\((-\infty, -1)\)
\(f^{\prime}(-2) = 3 \gt 0\) rostoucí

\((-1, +\infty)\)
\(f^{\prime}(0) = 3 \gt 0\) rostoucí

Závěr:

Příklad 7

Určete intervaly monotónnosti funkce \(f: y = 3x+\ln(x+2)\).

Řešení

Intervaly spojitosti: \((-2, +\infty)\).
Derivace: \(f^{\prime}(x) = 3+\Large\frac{1}{x+2}\), pro \(x \gt -2\).
Poznámka: Všimněte si, že \(\Large\frac{1}{x+2}\) je pro \(x \gt -2\) vždy kladné.
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti (řešení rovnice \(3+\Large\frac{1}{x+2}\normalsize = 0\) pro \(x \gt -2\)): žádné.
Tabulka:

\((-2, +\infty)\)
\(f^{\prime}(-1) = 4 \gt 0\) rostoucí

Závěr: Funkce \(f\) je rostoucí na intervalu \((-2, +\infty)\).

Úloha 8

Určete intervaly monotónnosti funkce \(f: y = 2x+e^{3x}\).

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = 2+3e^{3x}\).
Poznámka:
Body z intervalů spojitosti, v nichž není derivace definována: žádné.
Stacionární body z intervalů spojitosti
Tabulka:

\((-\infty, +\infty)\)
\(f^{\prime}(0) = 5 \gt 0\) rostoucí

Závěr:

Příklad 8

Určete intervaly monotónnosti funkce \(f: y = 4 - |x+1|\).

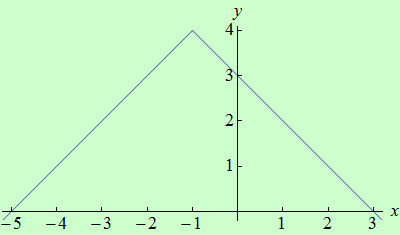graf funkce

Řešení

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace: \(f^{\prime}(x) = 1\) pro \(x \lt -1\) a \(f^{\prime}(x) = -1\) pro \(x \gt -1\).
Body z intervalů spojitosti, v nichž není derivace definována: \(-1\).
Stacionární body z intervalů spojitosti (řešení rovnice \(f^{\prime}(x) = 0\)): žádné.
Tabulka:

\((-\infty, -1)\)	\(-1\)	\((-1, +\infty)\)
\(f^{\prime}(-2) = 1 \gt 0\) rostoucí		\(f^{\prime}(0) = -1 \lt 0\) klesající

Závěr: Funkce \(f\) je rostoucí na intervalu \((-\infty, -1 \rangle \) a klesající na intervalu \( \langle {-1}, +\infty)\).

Úloha 9

Určete intervaly monotónnosti funkce \(f: y = |x-2|+3\).

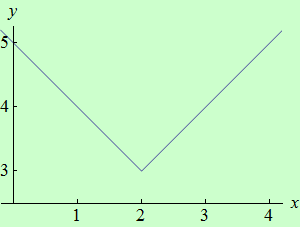graf funkce

Intervaly spojitosti: \((-\infty, +\infty)\).
Derivace:
Body z intervalů spojitosti, v nichž není derivace definována: \(2\).
Stacionární body z intervalů spojitosti
Tabulka:

\((-\infty, 2)\)	\(2\)	\((2, +\infty)\)
\(f^{\prime}(1) = -1 \lt 0\) klesající		\(f^{\prime}(3) = 1 \gt 0\) rostoucí

Závěr: