Back to homepage - zpet na domovskou stranku
Research papers and publications

Open Problems

The following problems are open, at least for me. The first person who provides me a correct complete solution (preferrably by e-mail) can be awarded by the mentioned prize. As a unit I use, according to Czech tradition, one beer. This means either one usual glass of Czech beer or one glass of Czech wine or one glass of apple juice. The prize may be received only in the Czech Republic.

Definition. A compact space K is called Valdivia if it is homeomorphic to some $K'\subset\Bbb R^\Gamma$ such that $\{x\in K' : \{\gamma\in\Gamma : x(\gamma)\ne0\}\text{ is countable}\}$ is dense in K'.

PROBLEM 1 (2 beers) Is there a scattered Valdivia compactum containing a copy of $[0,\omega_2]$?

A topological space is scattered if any its nonempty subset has a relatively isolated point.

PROBLEM 2 (Asked at 29th Winter School in Lhota nad Rohanovem, February 2001) Let $X=\ell_1([0,\pi/2])$ and $Y=\{x\in X: \sum\limits_{t\in[0,\pi/2]}x(t)\cos t=0\ \& \ \sum\limits_{t\in[0,\pi/2]}x(t)\sin t=0\}$. Is the dual unit ball of Y, in its weak* topology, a Valdivia compactum?
Possible answers:
a) No. (3 beers)
b) Yes, and the homeomorphism in the definition of a Valdivia compactum may be chosen linear. (2 beers)
c) Yes, but the homeomorphism cannot be chosen linear. (10 beers)

PROBLEM 3 (3 beers) Let K and L be nonempty compact spaces such that $K\times L$ is Valdivia. Are K and L Valdivia, too?
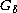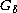Remark: Yes, if each one of them has at least one $G_\delta$-point (easy) or if at least one of them has a dense set of $G_\delta$-points (not easy).



CESKY - ISO 8859