


Next: Klasická kryptografie
Up: Kvantové algoritmy
Previous: Kvantové algoritmy
Obsah
Jak známo, Fourierova transformace mapuje funkce v časové doméně na funkce
frekvenčního spektra. Její hlavní vlastností z pohledu kvantové mechaniky je,
že mezi qubity vyvolává kvantovou interferenci, která je buď konstruktivní nebo
destruktivní. Konstruktivní interference v signálu zvýrazňuje jisté
charakteristiky (frekvence) nad charakteristikami jinými. Takovým způsobem
uvádí registr do stavu, v němž naměříme jeho hodnoty s různými
pravděpodobnostmi (tzn. ovlivňuje amplitudy pravděpodobností).
A právě tato vlastnost má zásadní vliv na praktickou
použitelnost některých algoritmů. Abychom vyhověli požadavku unitárnosti
operace definujeme kvantovou diskrétní Fourierovu transformaci (KFT) jako vývoj
registru
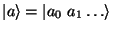 na
na
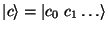 podle :
podle :
kde 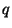 je počet stavů registru (
je počet stavů registru (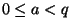 ) a
) a 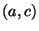 jsou souřadnice prvků
unitární matice a jsou rovny
jsou souřadnice prvků
unitární matice a jsou rovny
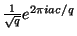 .
Tato matice (transformace) je základem faktorizačního algoritmu a nazývá se
.
Tato matice (transformace) je základem faktorizačního algoritmu a nazývá se
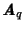 . Její sloupce a řádky jsou indexovány od nuly
jako celá čísla odpovídající binárním reprezentacím stavů.
Aby bylo možné navrhnout efektivní algoritmy založené na KFT, bylo nutné
samotnou KFT vymyslet efektivně. Shor takovou KFT navrhl pro
. Její sloupce a řádky jsou indexovány od nuly
jako celá čísla odpovídající binárním reprezentacím stavů.
Aby bylo možné navrhnout efektivní algoritmy založené na KFT, bylo nutné
samotnou KFT vymyslet efektivně. Shor takovou KFT navrhl pro 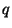 , které je
mocninou dvou (
, které je
mocninou dvou (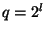 ). Pro její výpočet potřeboval jen
). Pro její výpočet potřeboval jen 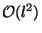 kvantových bran, kterých jsou dva typy. Jednou je Hadamardova brána definovaná
jako:
kvantových bran, kterých jsou dva typy. Jednou je Hadamardova brána definovaná
jako:
Tato brána vyvíjí stav 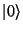 do vyvážené superpozice všech možných
do vyvážené superpozice všech možných 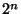 stavů (pokud je aplikována na
stavů (pokud je aplikována na 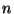 qubitů jako
qubitů jako
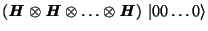 nazývá se Walsh-Hadamardova transformace W).
Hadamardovu bránu ovlivňující bit na pozici
nazývá se Walsh-Hadamardova transformace W).
Hadamardovu bránu ovlivňující bit na pozici 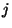 označujeme
označujeme
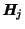 . Druhou použitou bránou je
. Druhou použitou bránou je
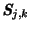 , která operuje s bity na pozicích
, která operuje s bity na pozicích 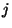 a
a 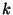 :
:
kde
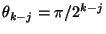 . K provedení KFT aplikujeme brány v pořadí
zleva doprava podle obecného schématu:
. K provedení KFT aplikujeme brány v pořadí
zleva doprava podle obecného schématu:
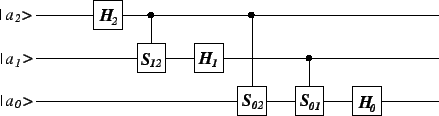
Například pro tři bity (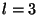 ) aplikujeme brány
) aplikujeme brány
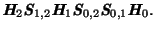 Tato operace vrací registr bitově převrácený, takže pro dokončení KFT je
zapotřebí výsledný registr bitově invertovat nebo jej číst z opačné strany,
což je již z hlediska implementace jednoduchá operace.
Tato operace vrací registr bitově převrácený, takže pro dokončení KFT je
zapotřebí výsledný registr bitově invertovat nebo jej číst z opačné strany,
což je již z hlediska implementace jednoduchá operace.
Obrázek:
Obvod kvantové Fourierovy transformace: pro 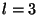 ; rekurzivně lze obvod rozšiřovat podle obecného vzorce. Jak je u kvantových obvodů zvykem, brány se provádějí zleva doprava, což odpovídá uvedenému zápisu. Lze si rovněž všimnout jak brány S
; rekurzivně lze obvod rozšiřovat podle obecného vzorce. Jak je u kvantových obvodů zvykem, brány se provádějí zleva doprava, což odpovídá uvedenému zápisu. Lze si rovněž všimnout jak brány S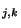 operují nad dvěma qubity.
operují nad dvěma qubity.
 |



Next: Klasická kryptografie
Up: Kvantové algoritmy
Previous: Kvantové algoritmy
Obsah
Bashar
2001-01-23
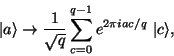
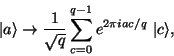

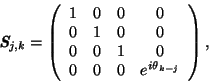

![]()
![]()
![]()
![]()