Question 5 - Collapse Example

We investigate the blow-up behaviour of the following ODE:

$\begin{array}{rl} x'(t) &= -x^{-\frac12}, \\ x(0) &= 1 \end{array}$

Contents

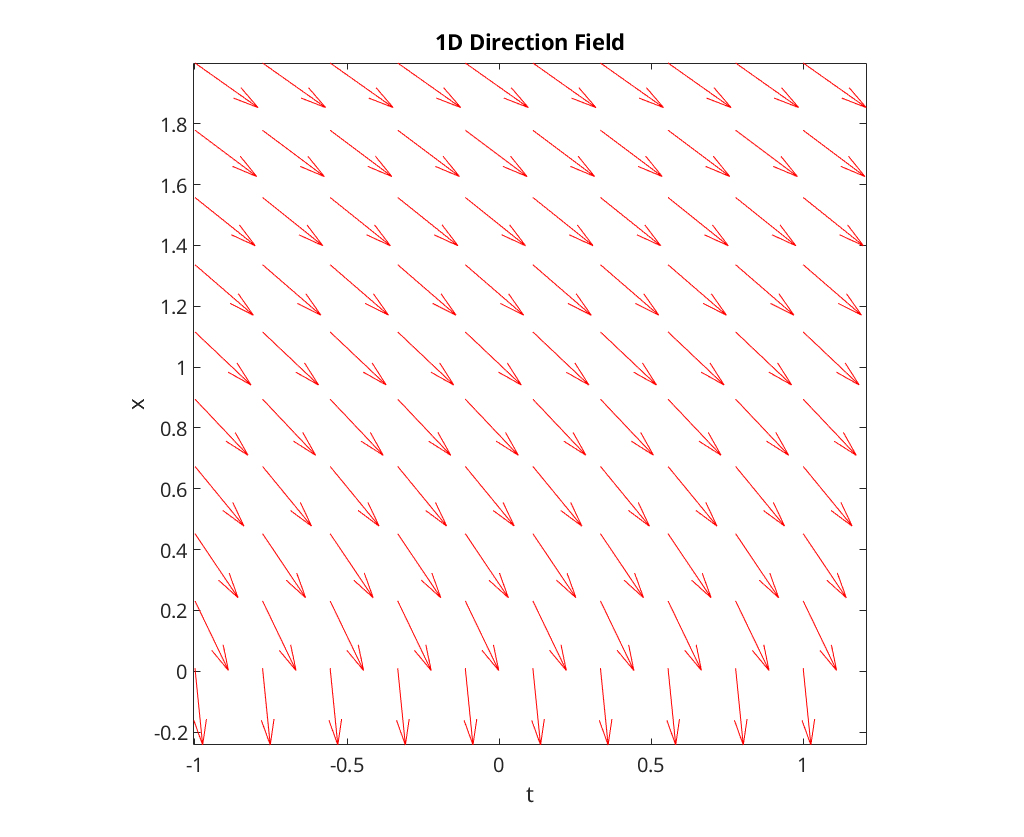
5(a) - Direction field

We first plot the direction field of the ODE over $t\in[-1,1]$ and $x\in[.01,2]$:

dirfield(@collapseex, -1, 1, .01, 2);

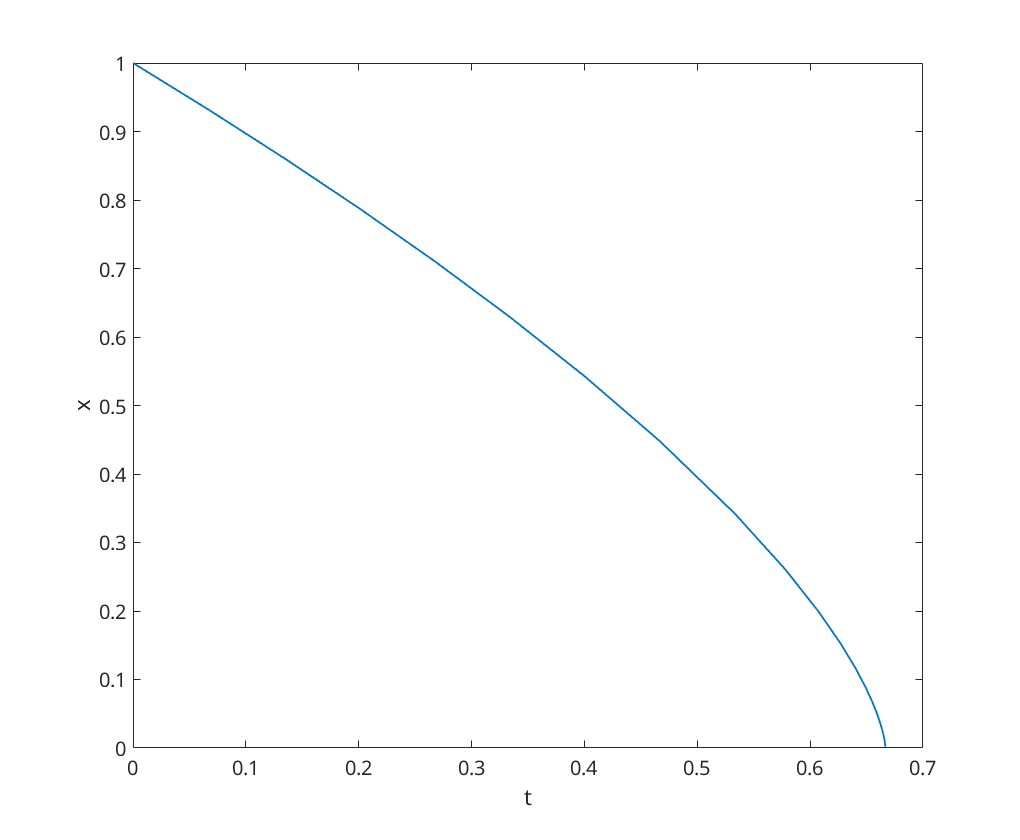
5(b) - Simulation over various time periods

We now simulate the ODE over the time period $t\in[0,\frac23]$ (which stops before the collapse will occur)

[t,x] = ode23(@collapseex, [0, 2/3], 1);

figure;
plot(t, x);
xlabel('t');
ylabel('x');

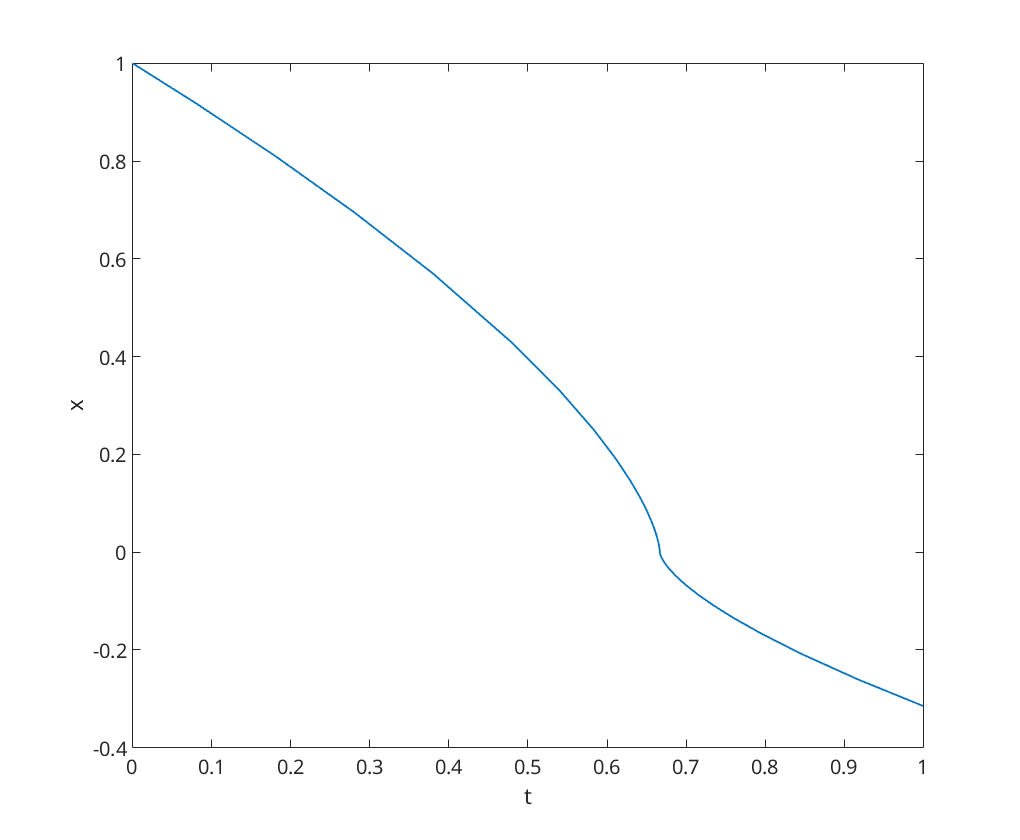
We now simulate the ODE over the time period $t\in[0,1]$ (which hits the blowup behaviour), we note that the solve completes, but the plot throws an error because the solution has complex parts

[t,x] = ode23(@collapseex, [0, 1], 1);

figure;
plot(t, x);
xlabel('t');
ylabel('x');

Warning: Imaginary parts of complex X and/or Y arguments ignored. 

Published with MATLAB® R2023a